지도학습 알고리즘¶
예제에 사용할 데이터¶
명령창에서 mglearn 모듈을 설치합니다. mglearn 모듈은 Introduction to Maching Learning with Python 책에서 사용하는 데이터와 그래프를 만드는데 편리한 기능을 제공합니다.
> pip install mglearn
wave 데이터¶
mglearn.plots.plot_knn_regression에 사용되는 데이터는 datasets.make_wave 함수로부터 만들어 집니다. make_wave 데이터는 균등 분포를 따르는 x 값과 사인 잡음이 들어간 정규분포의 y값으로 이루어집니다.
유방암 데이터¶
sklearn.datasets에 있는 유방암 데이터를 이용한다.
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
k-최근접 이웃¶
k-NN(k-Nearest Neighbors) 알고리즘은 주어진 훈련 집합과 새로운 데이터 사이에 가장 가까운 거리에 있는 이웃을 찾는 것입니다. 이웃이란 훈련 집합의 레이블을 의미합니다.
데이터 만들기¶
In [1]: from matplotlib import font_manager, rc
...: import matplotlib as mlp
...: font_name = font_manager.FontProperties(fname="c:/Windows/Fonts/malgun.ttf").get_name()
...: rc('font', family=font_name)
...: mlp.rcParams['axes.unicode_minus'] = False # 축에 음수 표시
...:
sklearn.datasets 의 make_classification 함수를 이용해서 분류 데이터를 만들 수 있습니다.
n_samples은 표본의 갯수이고n_features는 특징 전체의 갯수로n_informative,n_redundant,n_repeated의 갯수 및 (n_features - n_informative - n_redundant _ n_redundant)의 갯수로 이루어진 특징들로 구성됩니다.n_redundant는 informative 특징들의 랜덤 선형 결합으로 나타내는 특징의 갯수,n_repeated는 informative 와 redundant 특징들로부터 랜덤하게 뽑아낸 중복되는 특징들의 갯수,n_classes는 분류할 레이블(또는 클래스)의 갯수입니다.n_clusters_per_class는 클래스(또는 레이블) 당 군집의 갯수를 나타냅니다.
In [6]: from sklearn.datasets import make_classification
...: X, y = make_classification(n_samples=30, n_features=2, n_redundant=0, n_informative=1, n_clusters_per_class=1, n_classes=2, random_state=1)
...:
만든 데이터를 출력해봅니다.
In [8]: import matplotlib.pyplot as plt
...: fig, ax = plt.subplots()
...: ax.scatter(X[:, 0][y == 0], X[:, 1][y == 0], marker='o', label='훈련클래스 0');
...: ax.scatter(X[:, 0][y == 1], X[:, 1][y == 1], marker='^', label='훈련클래스 1');
...: ax.legend(loc='best')
...:
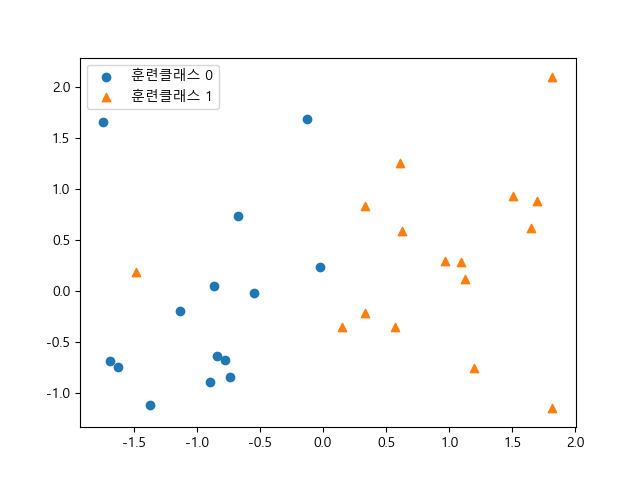
이웃의 갯수 n_neighbors=3으로 하고 테스트 데이터는 3개의 값을 설정합니다.
In [13]: n_neighbors=3
....: X_test = np.array([[0.1, 1.75], [-2.0, 0.5], [2.1, 1.75]])
....:
sklearn.metrics의 euclidean_distances 함수를 이용해서 훈련 집합 X와 테스트 집합 X_test 와의 유클리디안 거리 dist를 측정합니다. 다음에 np.argsort를 이용해 각 열의 거리가 가장 가까운 순으로 인덱스를 정렬합니다.
In [15]: from sklearn.metrics import euclidean_distances
....: dist = euclidean_distances(X, X_test)
....: closest = np.argsort(dist, axis=0)
....:
테스트 집합과 가장 가까운 거리에 있는 훈련 집합 3개의 원소와 선분으로 연결해봅니다.
In [18]: ax.scatter(X_test[:, 0], X_test[:, 1], c='gray', marker='*', s=60, label='테스트 집합')
....: for x, neighbors in zip(X_test, closest.T):
....: for neighbor in neighbors[:n_neighbors]:
....: ax.arrow(x[0], x[1], X[neighbor, 0] - x[0], X[neighbor, 1] - x[1], head_width=0, fc='gray', ec='gray')
....: ax.legend(loc='best')
....:
Out[18]: <matplotlib.collections.PathCollection at 0x156b9dc2668>
Out[19]: <matplotlib.legend.Legend at 0x156b9297cf8>
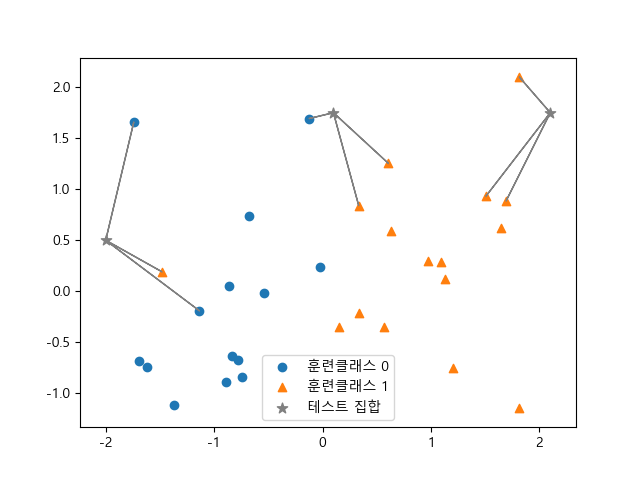
sklearn.neighbors 모듈의 KNeighborsClassifier 클래스를 이용해서 이웃의 갯수 n_neighbors=3을 인자로 건네면서 인스턴스 knn을 만듭니다. predict() 메소드를 이용해서 테스트 집합의 원소에 대한 예측값 y_pred을 구합니다.
In [20]: from sklearn.neighbors import KNeighborsClassifier
....: knn = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
....: y_pred = knn.predict(X_test)
....:
X_test[:, 0][y_pred == 0]를 이용하여 레이블 값이 0인 값들만 표시할 수 있습니다. ax.get_legend_handles_labels() 메소드를 이용하면 범례(legend)들을 편집할 수 있으면 그것을 ax.legend() 메소드에 대입함으로 변경된 범례를 표시할 수 있습니다.
In [23]: ax.scatter(X_test[:, 0][y_pred == 0], X_test[:, 1][y_pred == 0], c='C0', marker='*', s=60, label='테스트 예측 0');
....: ax.scatter(X_test[:, 0][y_pred == 1], X_test[:, 1][y_pred == 1], c='C1', marker='*', s=60, label='테스트 예측 1');
....: ax.axis('equal');
....: handles, labels = ax.get_legend_handles_labels();
....: handles.pop(2);
....: ax.legend(handles=handles, loc='best');
....:
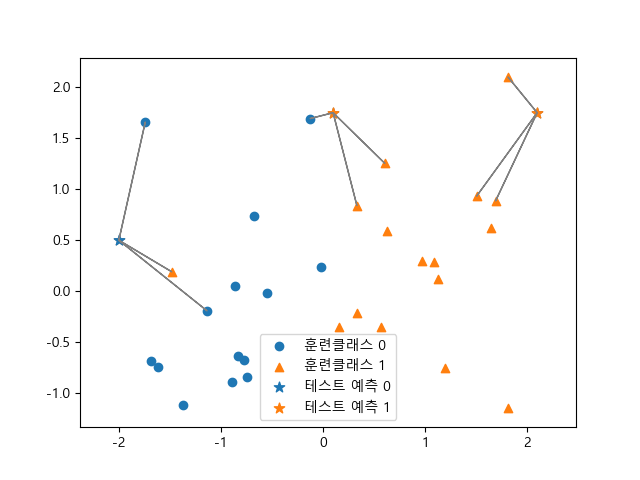
일반적인 접근을 시도해보겠습니다. 앞에서 사용했던 분류용 집합을 만들고 sklearn.model_selection의 train_test_split 메소드를 이용해서 훈련집합과 테스트 집합으로 분리합니다. 기본적으로 75%의 훈련 집합과 25%의 테스트 집합으로 분리합니다.
In [29]: from sklearn.datasets import make_classification
....: X, y = make_classification(n_samples=30, n_features=2, n_redundant=0, n_informative=1, n_clusters_per_class=1, n_classes=2, random_state=1)
....: from sklearn.model_selection import train_test_split
....: X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
....:
이웃이 3인 KNeighborsClassifier 클래스의 인스턴스를 만듭니다.
In [33]: from sklearn.neighbors import KNeighborsClassifier
....: knn = KNeighborsClassifier(n_neighbors=3)
....:
훈련 집합의 특징 행렬 X_train과 레이블 y_train을 이용하여 학습을 시킵니다.
In [35]: knn.fit(X_train, y_train)
Out[35]:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=3, p=2,
weights='uniform')
테스트 집합에 대해서 predict 메소드를 이용해서 예측을 합니다.
In [36]: y_pred = knn.predict(X_test)
....: y_pred
....:
Out[37]: array([1, 0, 0, 0, 1, 0, 1, 1])
모델의 일반화 정도를 보기 위해 score 메소드를 이용하여 정확도를 측정합니다.
In [38]: knn.score(X_test, y_test)
Out[38]: 0.875
약 88%의 정확도를 볼 수 있습니다. 즉, 테스트 집합 중 86%를 정확히 예측한 것을 알 수 있습니다.
KNeighborsClassifier 분석¶
이웃이 1, 3, 9개 일 때의 결정 경계를 확인해 봅니다.
In [39]: import numpy as np
....: import matplotlib.pyplot as plt
....: from matplotlib.colors import ListedColormap
....: fig, axes = plt.subplots(1, 3, figsize=(10, 3))
....: # Create color maps
....: cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
....: cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
....: h = .02
....: for n_neighbors, ax in zip([1, 3, 9], axes):
....: knn = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
....: x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
....: y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
....: xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
....: Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
....: # Put the result into a color plot
....: Z = Z.reshape(xx.shape)
....: ax.pcolormesh(xx, yy, Z, cmap=cmap_light)
....: # Plot also the training points
....: ax.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold, edgecolor='k', s=20)
....: ax.set_xlim(xx.min(), xx.max())
....: ax.set_ylim(yy.min(), yy.max())
....: ax.set_title("{} 이웃".format(n_neighbors))
....:
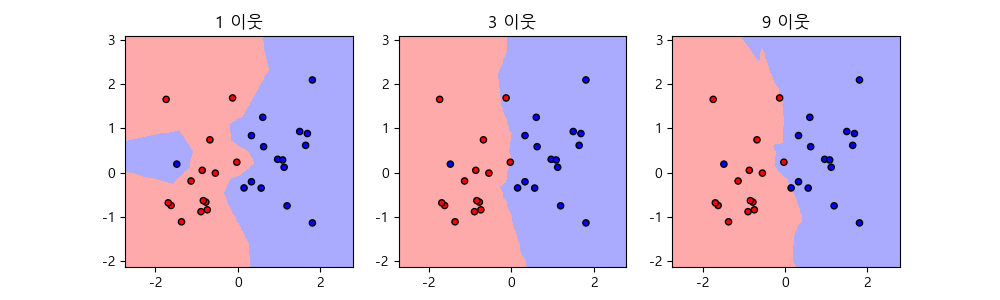
이웃이 하나일 때는 훈련 집합에 복잡하게 적합을 하는 것을 볼 수 있고 이웃이 3개일 때는 부드러운 경계를 가지면서 정확도는 떨어지는 것을 알 수 있습니다.
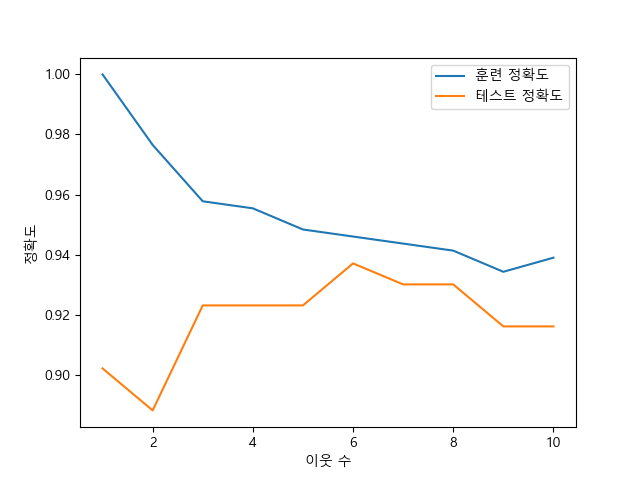
유방암 데이터 집합을 가지고 훈련 집합과 테스트 집합 사이의 일반화에 대한 그래프를 살펴보겠습니다.
In [48]: from sklearn.datasets import load_breast_cancer
....:
....: fig, ax = plt.subplots()
....: cancer = load_breast_cancer()
....: X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=66)
....:
....: training_accuracy = []
....: test_accuracy = []
....: # try n_neighbors from 1 to 10
....: neighbors_settings = range(1, 11)
....:
....: for n_neighbors in neighbors_settings:
....: # build the model
....: clf = KNeighborsClassifier(n_neighbors=n_neighbors)
....: clf.fit(X_train, y_train)
....: # record training set accuracy
....: training_accuracy.append(clf.score(X_train, y_train))
....: # record generalization accuracy
....: test_accuracy.append(clf.score(X_test, y_test))
....:
....: ax.plot(neighbors_settings, training_accuracy, label="훈련 정확도")
....: ax.plot(neighbors_settings, test_accuracy, label="테스트 정확도")
....: ax.set_ylabel("정확도")
....: ax.set_xlabel("이웃 수")
....: ax.legend()
....:
Out[57]: [<matplotlib.lines.Line2D at 0x156b95499e8>]
Out[58]: [<matplotlib.lines.Line2D at 0x156b9549eb8>]
Out[59]: Text(0,0.5,'정확도')
Out[60]: Text(0.5,0,'이웃 수')
Out[61]: <matplotlib.legend.Legend at 0x156b9549908>
k-최근접 이웃 회귀¶
k-최근접 알고리즘은 회귀 분석에도 사용할 수 있습니다.
In [62]: import mglearn
....: mglearn.plots.plot_knn_regression()
....:
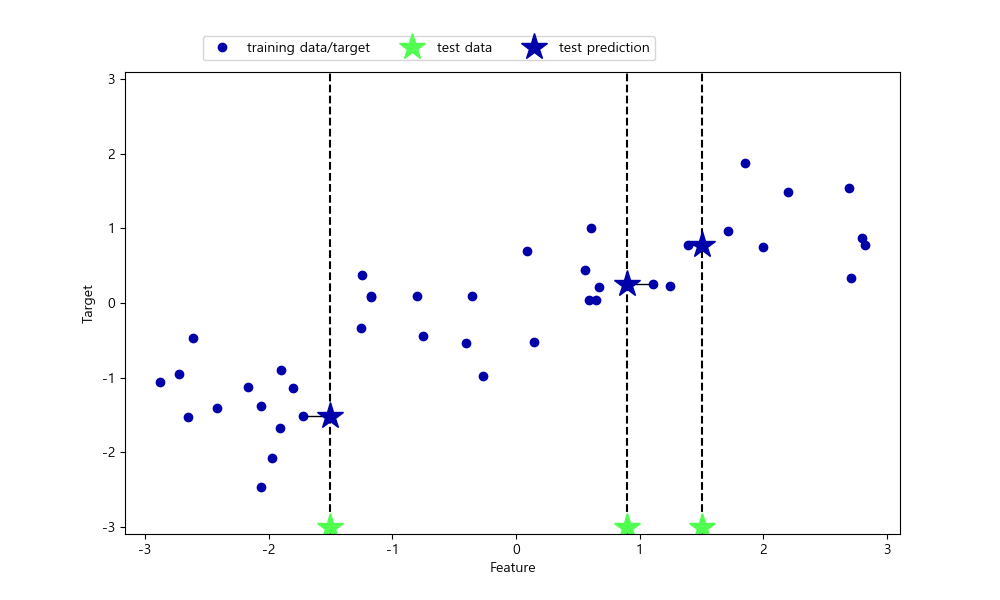
이웃이 한 개일 때는 가장 가까운 이웃의 목표값이 예측값이 됩니다.
In [64]: import mglearn
....: mglearn.plots.plot_knn_regression(n_neighbors=3)
....:
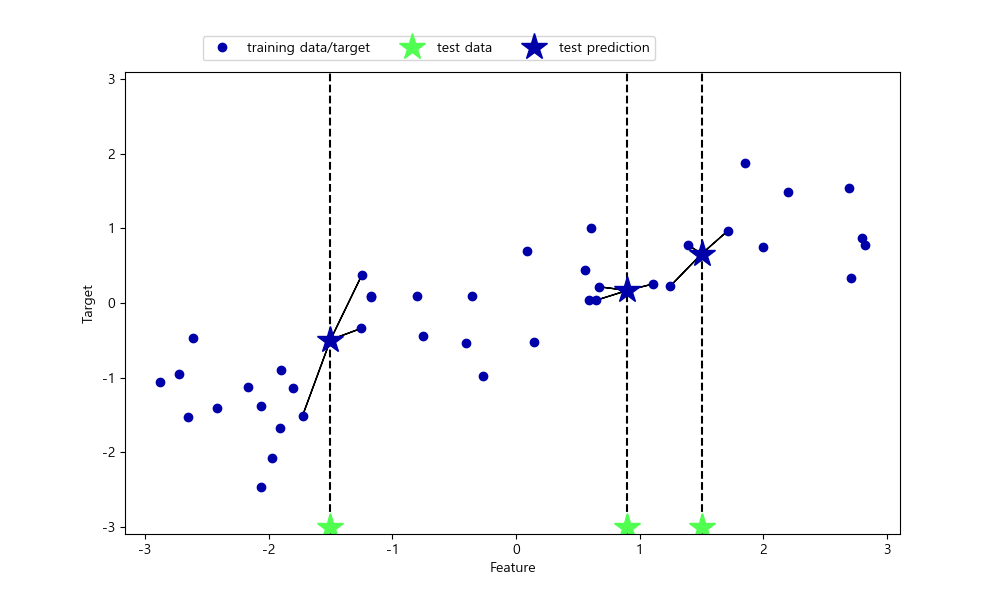
scikit-learn에서 회귀를 위한 k-최근접 이웃 알고리즘은 KNeighborsRegressor에 구현되어 있습니다.
In [66]: from sklearn.neighbors import KNeighborsRegressor
....: X, y = mglearn.datasets.make_wave(n_samples=40)
....: X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
....: reg = KNeighborsRegressor(n_neighbors=3)
....: reg.fit(X_train, y_train)
....:
Out[70]:
KNeighborsRegressor(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=3, p=2,
weights='uniform')
In [71]: y_pred = reg.predict(X_test)
....: y_pred
....:
Out[72]:
array([-0.05396539, 0.35686046, 1.13671923, -1.89415682, -1.13881398,
-1.63113382, 0.35686046, 0.91241374, -0.44680446, -1.13881398])
score 메소드를 이용해서 모델을 평가할 수 있습니다.
In [73]: reg.score(X_test, y_test)
Out[73]: 0.8344172446249604
반환값은 결정계수 \(R^2\) 값입니다. 결정계수는 0과 1사이의 값으로 0은 훈련 집합의 y_train의 평균값으로 예측하는 것을 의미하고 1은 예측 완벽한 것을 의미합니다.
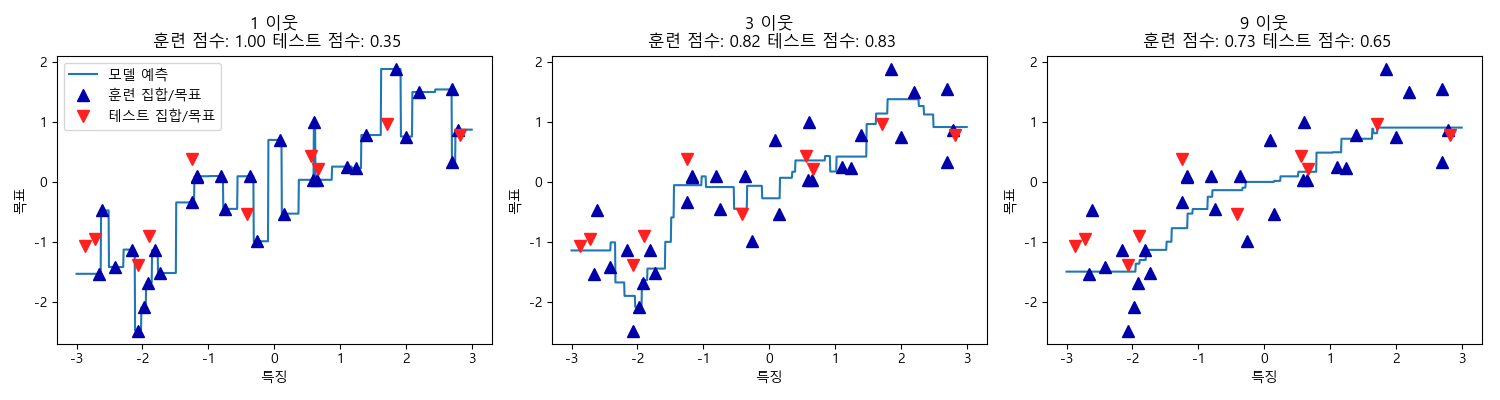
KNeighborsRegressor 분석¶
In [74]: fig, axes = plt.subplots(1, 3, figsize=(15, 4))
....: # create 1,000 data points, evenly spaced between -3 and 3
....: line = np.linspace(-3, 3, 1000).reshape(-1, 1)
....: for n_neighbors, ax in zip([1, 3, 9], axes):
....: # make predictions using 1, 3, or 9 neighbors
....: reg = KNeighborsRegressor(n_neighbors=n_neighbors)
....: reg.fit(X_train, y_train)
....: ax.plot(line, reg.predict(line))
....: ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
....: ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
....: ax.set_title("{} 이웃\n 훈련 점수: {:.2f} 테스트 점수: {:.2f}".format(n_neighbors, reg.score(X_train, y_train), reg.score(X_test, y_test)))
....: ax.set_xlabel("특징")
....: ax.set_ylabel("목표")
....: axes[0].legend(["모델 예측", "훈련 집합/목표", "테스트 집합/목표"], loc="best")
....: fig.tight_layout()
....:
요약¶
k-최근접 이웃의 이웃의 갯수는 보통 3 ~ 5정도일 때 잘 작동하지만 데이터에 영향을 받으므로 잘 조정해야 합니다.
knn은 이해하기 쉬워서 복잡한 알고리즘을 적용하기 전에 시도해볼 수 있는 알고리즘입니다. 그렇지만 특징의 갯수가 많거나 표본의 갯수가 많으면 느려집니다. 또한 특성값이 0으로 가득찬 희소 행렬의 경우는 잘 작동하지 않습니다. 실제 응용 문제에는 잘 사용되질 않습니다.
선형 모델¶
선형 모델은 다음과 같은 선형 함수를 만들어 예측에 사용합니다.
\(x_i\)는 데이터 특징에 대응되는 값이고 \(w_i\) 와 \(b\)는 모델이 학습해서 찾아낼 매개변수입니다. 여기서 \(i = 0, \ldots, p\)입니다. 여기서 \(\hat{y}\)은 \(p+1\) 차원에서 초평면(hyperplane)이라고도 합니다.
1차원 wave 데이터 집합을 직선으로 학습시키면 다음과 같습니다.
In [78]: mglearn.plots.plot_linear_regression_wave()
w[0]: 0.393906 b: -0.031804
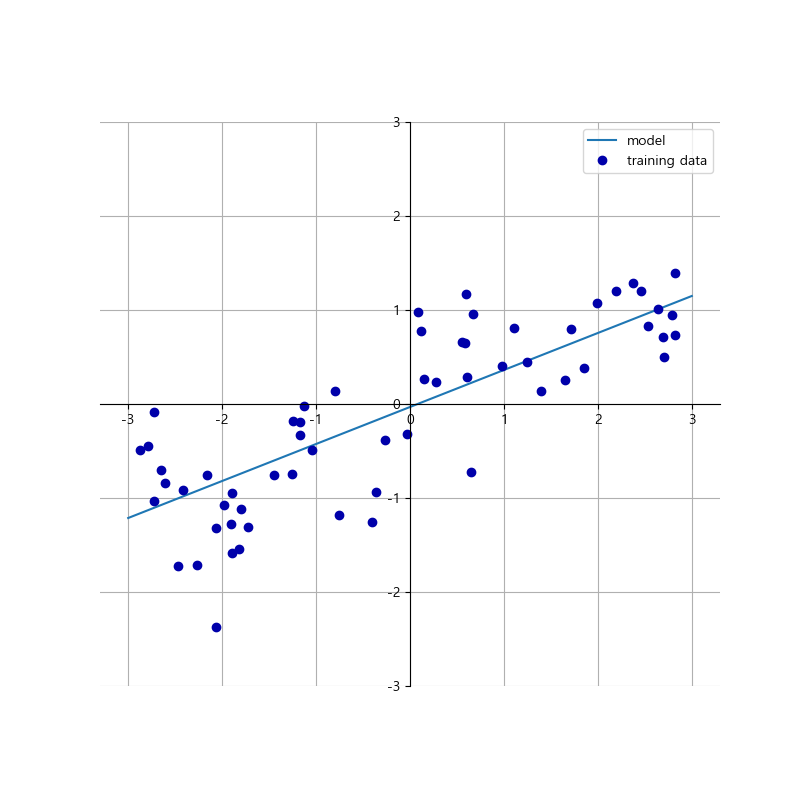
선형 회귀(최소 제곱법)¶
선형 회귀는 훈련 집합과 목표와의 평균 제곱 오차(mean squared error)를 최소화하도록 매개변수 \(w_i, b\)들을 찾는 것입니다.
wave 데이터를 가지고 예를 들어 봅니다.
In [79]: from sklearn.linear_model import LinearRegression
....: X, y = mglearn.datasets.make_wave(n_samples=60)
....: X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
....:
....: lr = LinearRegression().fit(X_train, y_train)
....:
선형 회귀 클래스 LinearRegression을 이용해 학습을 시켜서 나온 객체 lr은 가중치 \(w_i\)를 coef_ 속성에 저장하고 편향(또는 절편)을 intercept_ 속성에 저장합니다.
In [83]: print("가중치: {}, 절편: {}".format(lr.coef_, lr.intercept_))
가중치: [0.39390555], 절편: -0.031804343026759746
wave 데이터는 특징 열이 하나이므로 coef_도 하나밖에 없습니다. coef_는 특징열의 갯수만큼의 넘파이 배열로 나옵니다.
훈련 집합과 테스트 집합의 정확도를 확인해 봅니다.
In [84]: print("훈련 집합 정확도: {:.2f}, 테스트 집합 정확도: {:.2f}".format(lr.score(X_train, y_train), lr.score(X_test, y_test)))
훈련 집합 정확도: 0.67, 테스트 집합 정확도: 0.66
score는 \(R^2\)을 반환합니다. 훈련 집합과 테스트 집합의 점수가 0.66 정도로 그리 좋지 않습니다.
특성이 많은 보스턴 주택가격 데이터 집합을 가지고 LinearRegression 모델을 평가해봅니다. 이 데이터 집합은 104개의 특징열을 가지고 있습니다.
In [85]: X, y = mglearn.datasets.load_extended_boston()
....: X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
....:
....: lr = LinearRegression().fit(X_train, y_train)
....:
score를 살펴보면 훈련 집합의 점수는 높은데 테스트 집합의 점수가 매우 낮은 것을 알 수 있습니다.
In [88]: print("훈련 집합 정확도: {:.2f}, 테스트 집합 정확도: {:.2f}".format(lr.score(X_train, y_train), lr.score(X_test, y_test)))
훈련 집합 정확도: 0.95, 테스트 집합 정확도: 0.61
이것은 모델이 훈련 집합에 과대적합 되었다는 추정을 할 수 있습니다. 따라서 모델의 복잡도를 제어할 모델을 사용해야 합니다.
릿지(Ridge) 회귀¶
일반적인 규제가 적용된 목적함수는 다음과 같이 표시할 수 있습니다. \(\Theta\)는 학습을 통해 찾아야 할 가중치 변수들에 대한 벡터이고 \(\mathbb{X}\)는 특징 행렬, \(\mathbb{Y}\)는 목표(target) 벡터를 의미합니다.
다음은 릿지 회귀 목적함수입니다. \(\alpha\)를 크게하면 가중치 변수들의 효과를 제한할 수 있고 작게하면 가중치의 효과가 증대합니다.
릿지 회귀를 이용하여 확장된 보스턴 주택가격 데이터에 적용해봅니다.
In [89]: from sklearn.linear_model import Ridge
....:
....: ridge = Ridge().fit(X_train, y_train)
....: print("훈련 집합 점수: {:.2f}, 테스트 집합 점수: {:.2f}".format(ridge.score(X_train, y_train), ridge.score(X_test, y_test)))
....:
훈련 집합 점수: 0.89, 테스트 집합 점수: 0.75
릿지 인스턴스를 만들 때 \(\alpha=1.0\)이 기본값입니다. 선형 회귀 모델보다는 테스트 점수가 향상된 것을 확인할 수 있습니다.
훈련 집합의 크기와 성능 점수(\(R^2\))와의 관계를 다음과 같이 그래프로 확인해봅니다. Ridge와 LinearRegression 모델에 대해서 훈련 집합의 크기를 변화시키면서 점수를 표시합니다. 둘 다 데이터의 크기가 커지면 점수가 높아지는 것을 볼 수 있습니다. LinearRegression의 훈련 점수가 Ridge 훈련 점수보다 높게 나타나는 것을 알 수 있습니다. 하지만 테스트 점수는 Ridge 모델에서 더 높게 나오는 것을 알 수 있습니다. 즉, 규제를 적당히 주어질 때 테스트 집합에 잘 적합되고 있는 것을 알 수 있습니다.
In [92]: plt.clf()
....: mglearn.plots.plot_ridge_n_samples()
....:
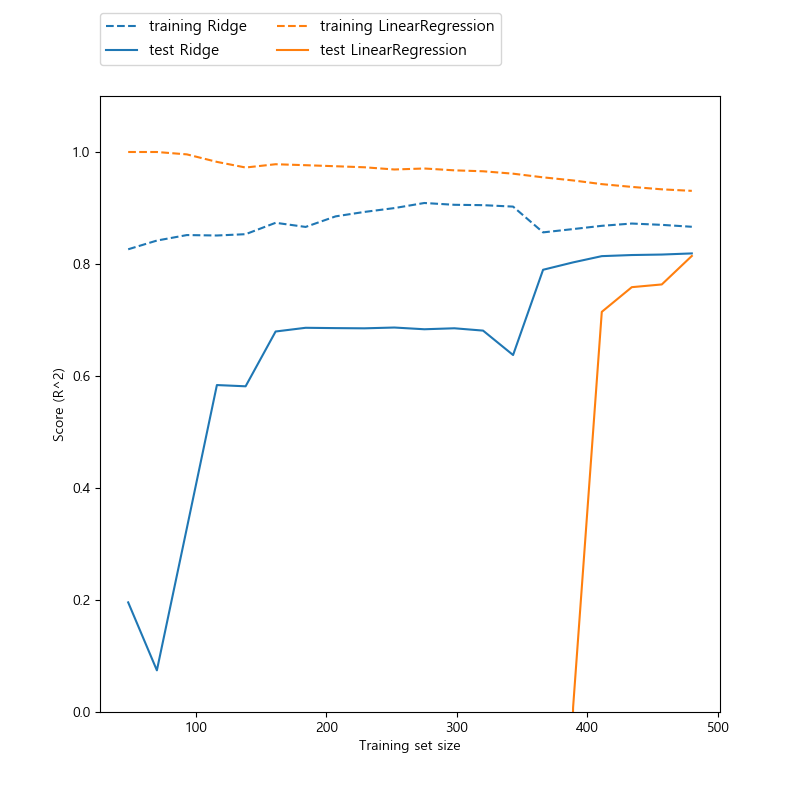
라쏘¶
라쏘 모델은 릿지 모델의 \(L_2\) norm 규제항 대신에 \(L_1\) norm을 사용합니다.
라쏘 모델의 특성으로 학습을 하면 0이 되는 가중치가 많다는 것입니다. 이것은 특징열을 선택하는 결과가 됩니다. 보스턴 주택가격 데이터에 라쏘를 적용해봅니다.
In [94]: from sklearn.linear_model import Lasso
....:
....: lasso = Lasso().fit(X_train, y_train)
....: print("훈련 집합 점수: {:.2f}, 테스트 집합 점수: {:.2f}".format(lasso.score(X_train, y_train), lasso.score(X_test, y_test)))
....: print("사용된 특징의 수: {}".format(np.sum(lasso.coef_ != 0)))
....:
훈련 집합 점수: 0.29, 테스트 집합 점수: 0.21
사용된 특징의 수: 4
결과가 좋지 않은 것을 알 수 있습니다. 특징의 갯수는 104개인데 사용된 특징의 수는 4개로서 과소적합되었다는 것을 알 수 있습니다. 라쏘에서도 \(\alpha\)를 이용해서 가중치를 조정할 수 있습니다. \(\alpha\)가 작으면 규제가 작아지고 커지면 규제가 커집니다. 기본값은 1.0입니다. 값을 0.01로 조정해봅니다.
In [98]: lasso01 = Lasso(alpha=0.01, max_iter=1000000).fit(X_train, y_train)
....: print("훈련 집합 점수: {:.2f}, 테스트 집합 점수: {:.2f}".format(lasso01.score(X_train, y_train), lasso01.score(X_test, y_test)))
....: print("사용된 특징의 수: {}".format(np.sum(lasso01.coef_ != 0)))
....:
훈련 집합 점수: 0.90, 테스트 집합 점수: 0.77
사용된 특징의 수: 33
사용된 특징의 갯수가 33개이고 테스트 집합에 대한 점수도 릿지보다 좋아진 것을 알 수 있습니다. alpha=0.0001 일 때는 0.01 일 때보다 테스트 점수가 더 낮아지는 걸 확인할 수 있습니다.
In [101]: lasso0001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
.....: print("훈련 집합 점수: {:.2f}, 테스트 집합 점수: {:.2f}".format(lasso0001.score(X_train, y_train), lasso0001.score(X_test, y_test)))
.....: print("사용된 특징의 수: {}".format(np.sum(lasso0001.coef_ != 0)))
.....:
훈련 집합 점수: 0.95, 테스트 집합 점수: 0.64
사용된 특징의 수: 94
alpha=1 일때 대부분의 계수는 0이고 나머지 계수도 0에 가까운 것을 알 수 있고 alpha가 줄어들면 계수들이 커지는 것을 알 수 있습니다.
In [104]: plt.cla()
.....: plt.plot(lasso.coef_, 's', label="라쏘 alpha=1")
.....: plt.plot(lasso01.coef_, '^', label="라쏘 alpha=0.01")
.....: plt.plot(lasso0001.coef_, 'v', label="라쏘 alpha=0.0001")
.....: plt.legend(ncol=2, loc=(0, 1.05))
.....:
Out[105]: [<matplotlib.lines.Line2D at 0x156bbab15f8>]
Out[106]: [<matplotlib.lines.Line2D at 0x156bbab1a90>]
Out[107]: [<matplotlib.lines.Line2D at 0x156bbaa9080>]
Out[108]: <matplotlib.legend.Legend at 0x156bbad07f0>
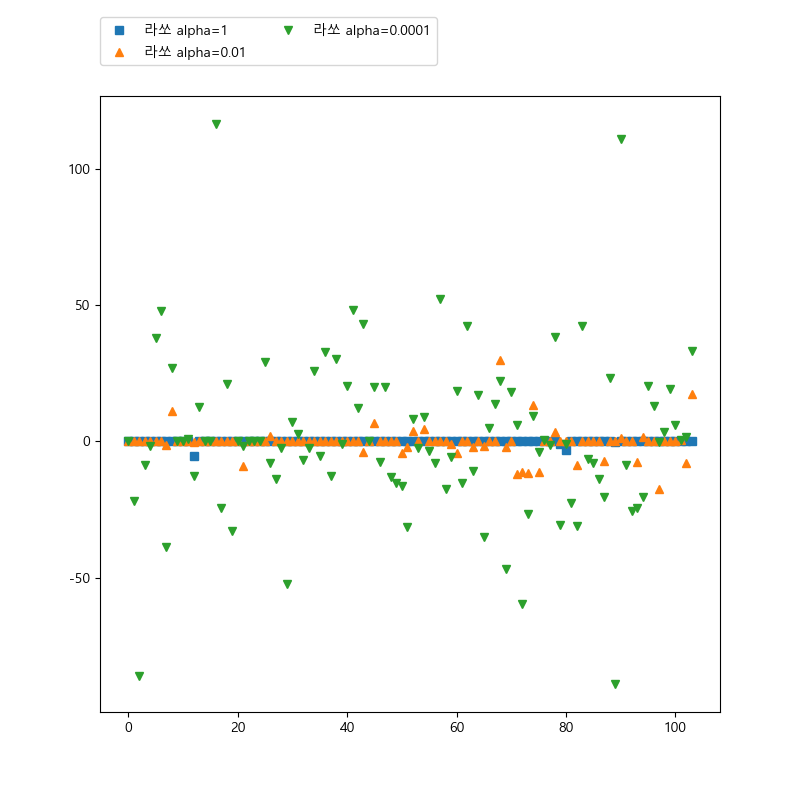
분류형 선형 모델¶
선형 모델은 분류에도 사용할 수 있습니다. 선형 회귀에서 사용한 것과 같은 식을 사용합니다.
이진 분류에서는 \(\hat{y} > 0\) 이면 +1, \(\hat{y} < 0\) 이면 -1로 예측합니다. 초평면을 기준으로 두 개의 클래스로 분류합니다.
잘 알려진 선형 분류 알고리즘으로 로지스틱 회귀(logistic regression)와 서포트 벡터 머신(support vector machine)이 있습니다. 두 알고리즘을 forge 데이터에 적용을 해서 결정경계를 그림으로 그려봅니다.
In [109]: from sklearn.linear_model import LogisticRegression
.....: from sklearn.svm import LinearSVC
.....:
.....: X, y = mglearn.datasets.make_forge()
.....:
.....: fig, axes = plt.subplots(1, 2, figsize=(10, 3))
.....:
.....: for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
.....: clf = model.fit(X, y)
.....: mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5, ax=ax, alpha=0.7)
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
.....: ax.set_title("{}".format(clf.__class__.__name__))
.....: ax.set_xlabel("특성 0")
.....: ax.set_ylabel("특성 1")
.....: axes[0].legend()
.....: plt.tight_layout()
.....:
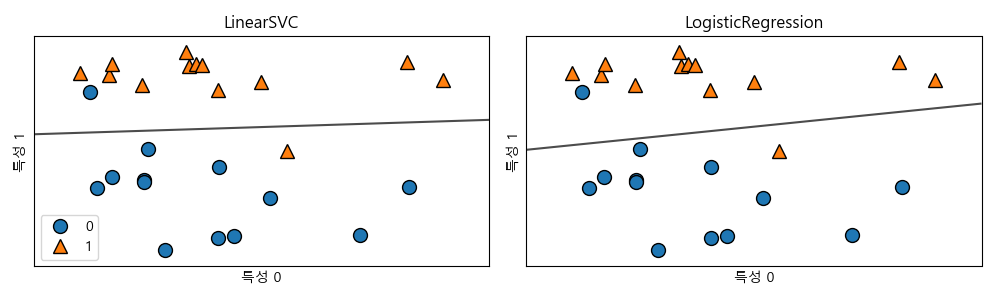
mglearn.plots.plot_2d_separator 함수는 결정경계를 표시하고 discrete_scatter는 넘겨진 자료의 산점도를 그립니다. 위 그림에서 결정경계의 위쪽은 클래스 1로 아래쪽은 클래스 0으로 분류했습니다. 새로운 데이터가 입력되어 위쪽에 있으면 1로 아래쪽에 있으면 0으로 분류합니다. 이 두 모델은 기본적으로 L2 규제를 사용합니다.
두 모델의 규제의 강도를 결정하는 인자는 C를 사용합니다. C의 값이 높아지면 규제는 감소하고 낮아지면 규제가 강해집니다. 즉, 높은 C값은 규제가 감소해서 훈련 집합에 최대한 맞추려고 하고 C값을 낮추면 모델의 계수가 0에 가까워져 규제가 강해집니다.
In [114]: mglearn.plots.plot_linear_svc_regularization()
.....: plt.tight_layout()
.....:
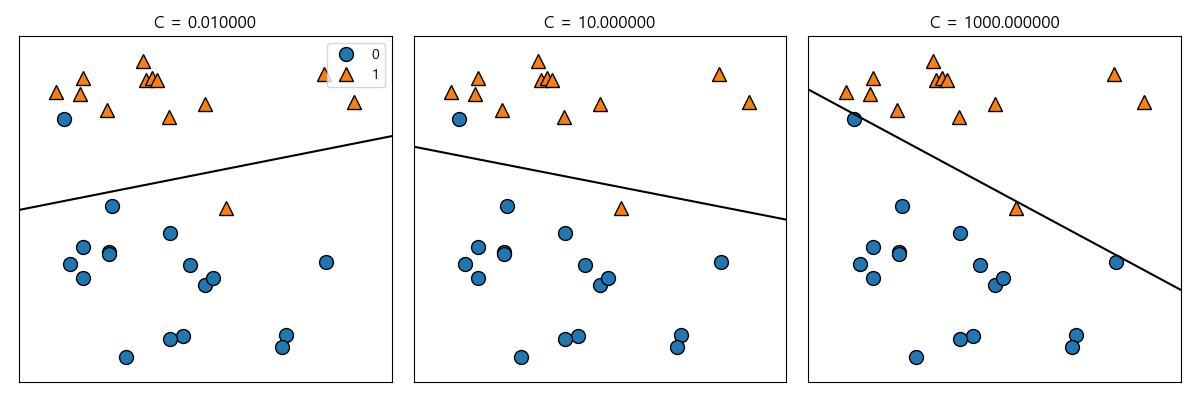
유방암 데이터를 이용해서 LogisticRegression을 자세히 분석해 봅니다.
In [116]: from sklearn.datasets import load_breast_cancer
.....: cancer = load_breast_cancer()
.....: X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42)
.....: logreg = LogisticRegression().fit(X_train, y_train)
.....: print("훈련 집합 점수: {:.3f}, 테스트 집합 점수: {:.3f}".format(logreg.score(X_train, y_train), logreg.score(X_test, y_test)))
.....:
훈련 집합 점수: 0.955, 테스트 집합 점수: 0.958
C=1 일 때 훈련 집합과 테스트 집합의 점수가 95%로 높게 나온 것을 보면 성능이 좋은 것을 알 수 있습니다. 그런데 비슷한 점수를 가지는 것으로보아 과소적합의 경향을 보인다고 할 수 있습니다. 규제를 약하게 하기위해 C를 높게 해보겠습니다.
In [121]: logreg100 = LogisticRegression(C=100).fit(X_train, y_train)
.....: print("훈련 집합 점수: {:.3f}, 테스트 집합 점수: {:.3f}".format(logreg100.score(X_train, y_train), logreg100.score(X_test, y_test)))
.....:
훈련 집합 점수: 0.972, 테스트 집합 점수: 0.965
C=100일 때 훈련 점수와 테스트 점수가 모두 나아진 것을 보면 규제가 약할 수록 학습이 잘되고 일반화가 잘된다는 것을 알 수 있습니다. C=0.01을 사용하면 어떻게 되는지 살펴봅니다.
In [123]: logreg01 = LogisticRegression(C=.01).fit(X_train, y_train)
.....: print("훈련 집합 점수: {:.3f}, 테스트 집합 점수: {:.3f}".format(logreg01.score(X_train, y_train), logreg01.score(X_test, y_test)))
.....:
훈련 집합 점수: 0.934, 테스트 집합 점수: 0.930
C=1일 때보다 둘 다 낮은 점수를 갖는 것을 확인할 수 있습니다.
In [125]: fig, ax = plt.subplots()
.....: ax.plot(logreg100.coef_.T, '^', label="C=100");
.....: ax.plot(logreg.coef_.T, 'o', label="C=1");
.....: ax.plot(logreg01.coef_.T, 'v', label="C=0.01");
.....: ax.set_xticks(range(cancer.data.shape[1]));
.....: ax.set_xticklabels(cancer.feature_names, rotation=90);
.....: ax.hlines(0, 0, cancer.data.shape[1]);
.....: ax.set_ylim(-5, 5);
.....: ax.set_xlabel("특성");
.....: ax.set_ylabel("계수 크기");
.....: ax.legend();
.....: fig.tight_layout()
.....:
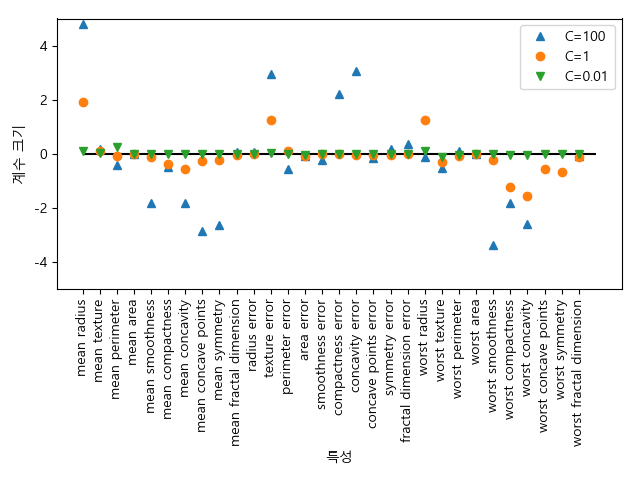
L1 규제를 이용하여 계수 그래프를 그려봅니다.
In [137]: ax.cla()
.....: for C, marker in zip([0.001, 1, 100], ['o', '^', 'v']):
.....: lr_l1 = LogisticRegression(C=C, penalty='l1').fit(X_train, y_train)
.....: print("C={:.3f}인 L1 로지스틱 회귀 훈련 점수: {:.2f}".format(C, lr_l1.score(X_train, y_train)))
.....: print("C={:.3f}인 L1 로지스틱 테스트 훈련 점수: {:.2f}".format(C, lr_l1.score(X_test, y_test)))
.....: ax.plot(lr_l1.coef_.T, marker, label="C={:.3f}".format(C));
.....: ax.set_xticks(range(cancer.data.shape[1]));
.....: ax.set_xticklabels(cancer.feature_names, rotation=90);
.....: ax.hlines(0, 0, cancer.data.shape[1])
.....: ax.set_xlabel("특성")
.....: ax.set_ylabel("계수 크기")
.....: ax.set_ylim(-5, 5)
.....: ax.legend(loc=3)
.....:
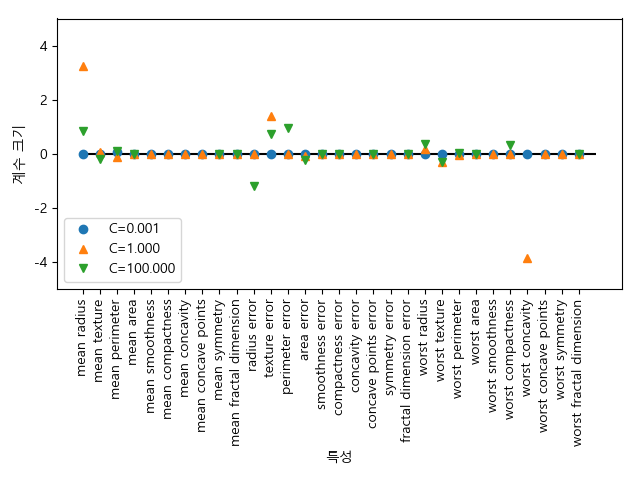
L1 규제를 사용하니 특징들의 갯수가 현저히 준 것을 확인할 수 있습니다.
다중 클래스 분류용 선형 모델¶
많은 선형 모델들은 기본적으로 이진 분류만을 지원합니다. 이진 분류 알고리즘을 이용해 다중 클래스 분류하는 방법은 일대나머지(one-to-rest) 방법을 이용하는 것입니다. 일대나머지 방법은 각 클래스를 다른 모든 클래스와 구분되도록 모델을 학습하는 것입니다.
3개의 클래스를 가진 간단한 데이터에 일대다 방식을 적용해봅니다. 이 데이터는 특징은 2차원이며 각 클래스의 데이터는 정규분포를 따릅니다. 위에서 \(p=2\)일 때이며 3차원 공간에서 평면을 의미합니다.
In [139]: from sklearn.datasets import make_blobs
.....:
.....: X, y = make_blobs(random_state=42)
.....: ax.cla()
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y);
.....: ax.set_xlabel("특성 0");
.....: ax.set_ylabel("특성 1");
.....: ax.legend(["클래스 0", "클래스 1", "클래스 2"]);
.....:
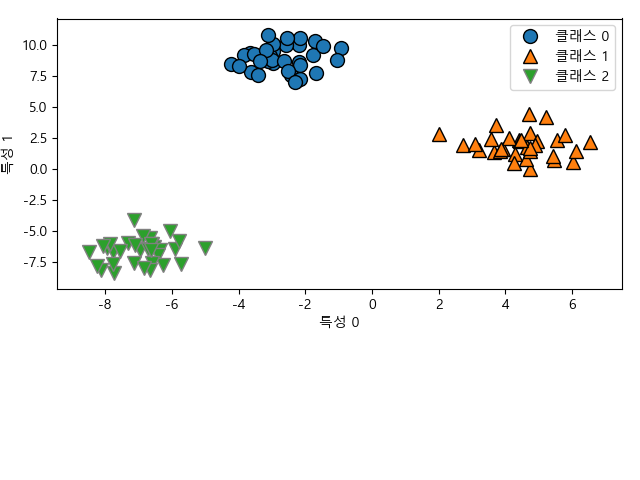
LinearSVC를 이용해 학습을 시켜보겠습니다.
In [146]: lin_svm = LinearSVC().fit(X, y)
.....: print("계수 배열 크기: {}".format(lin_svm.coef_.shape))
.....: print("절편 배열 크기: {}".format(lin_svm.intercept_.shape))
.....:
계수 배열 크기: (3, 2)
절편 배열 크기: (3,)
계수 배열은 클래스에 대응되는 3개의 벡터로 구성되고 각 벡터는 2차원 데이터에 대응되는 2개의 계수들로 이루어진 것을 알 수 있습니다. 절편은 각 클래스에 대응되는 값을 갖고 있습니다.
3개의 이진 분류기로 만든 경계를 시각화해봅니다. 평면의 방정식이 xy 평면과 만날 때 직선을 그린 것입니다.
In [149]: ax.cla()
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
.....: line = np.linspace(-15, 15)
.....: for coef, intercept, color in zip(lin_svm.coef_, lin_svm.intercept_, mglearn.cm3.colors):
.....: ax.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
.....: ax.set_ylim(-10, 15)
.....: ax.set_xlim(-10, 8)
.....: ax.set_xlabel("특성 0")
.....: ax.set_ylabel("특성 1")
.....: ax.legend(["클래스 0", "클래스 1", "클래스 2", "클래스 0 경계", "클래스 1 경계", "클래스 2 경계"], loc=(1.01, 0.3))
.....: fig.tight_layout()
.....:
Out[150]:
[<matplotlib.lines.Line2D at 0x156bc296f60>,
<matplotlib.lines.Line2D at 0x156bc296b38>,
<matplotlib.lines.Line2D at 0x156bc280d68>]
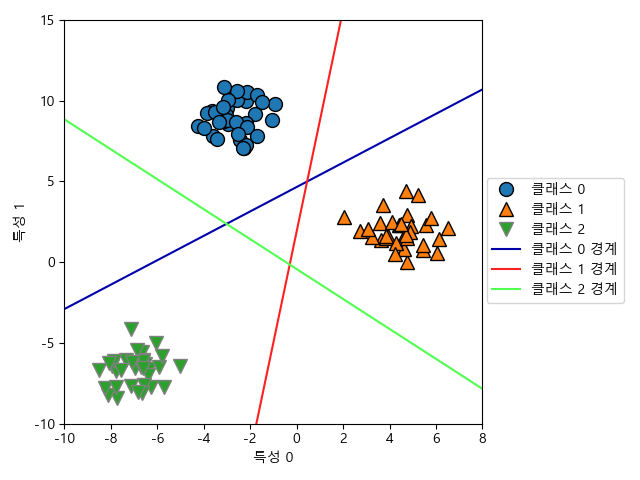
다음은 2차원 평면의 모든 점에서 예측한 것을 보여줍니다.
In [153]: ax.cla()
.....: mglearn.plots.plot_2d_classification(lin_svm, X, fill=True, alpha=0.7);
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y);
.....: line = np.linspace(-15, 15)
.....: for coef, intercept, color in zip(lin_svm.coef_, lin_svm.intercept_, mglearn.cm3.colors):
.....: ax.plot(line, -(line * coef[0] + intercept) / coef[1], c=color);
.....: ax.legend(["클래스 0", "클래스 1", "클래스 2", "클래스 0 경계", "클래스 1 경계", "클래스 2 경계"], loc=(1.01, 0.3));
.....: ax.set_xlabel("특성 0");
.....: ax.set_ylabel("특성 1");
.....:
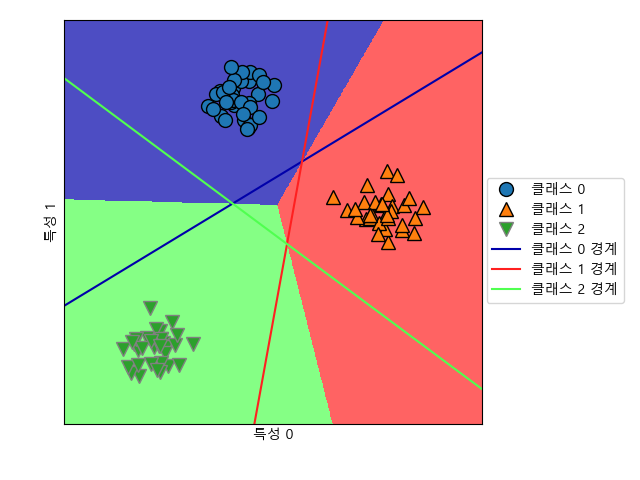
장단점¶
선형 모델의 주요 매개변수는 회귀 모델에서 alpha와 LinearSVC와 LogisticRegression에서 C입니다. alpha 값이 클수록, C 값이 작을수록 모델이 단순해집니다. 보통 C와 alpha는 로그 스케일로 최적치를 정합니다. L1 규제를 사용할 지 L2 규제를 사용할지는 중요한 특징의 갯수가 많으면 L2 그렇지 않으면 L1 규제를 사용합니다.
대용량의 데이터 집합이라면 Ridge에서 solver=”sag” 옵션을 사용하여 빠르게 처리하도록 할 수 있습니다. sag(Stochastic Average Gradient Descent) 방법을 사용한다는 것입니다. 다른 대안으로 대용량 처리 버전인 SGDClassifier와 SGDRegressor 등이 있습니다.
나이브 베이즈(Naive Bayes) 분류기¶
나이브 베이지에서 나이브(Naive)는 순진하다라는 뜻을 가지고 있습니다. 이런 수식어가 붙은 이유는 데이터 집합의 모든 특징들이 동등하고 독립적이라고 가정하기 때문입니다. 하지만 이런 가정에도 불구하고 분류학습에서 매우 정확한 결과 값을 내놓기 때문에 자주 사용되고 있습니다.
특징 벡터 \(\mathbf{x} = (x_1, x_2, \ldots, x_D)\)와 클래스(타깃) \(y = C_k\)가 주어졌다고 가정합니다. 특징 \(\mathbf{x}\)이 주어졌을 때 클래스 \(C_k\)가 나올 확률은 다음과 같습니다.
\(x_i\)들이 서로 조건부 독립이라는 순진한(naive) 가정하에서 다음과 같이 곱으로 표현할 수 있습니다.
따라서 다음과 같이 근사할 수 있습니다.
베르누이(Bernoulli) 나이브 베이즈¶
베르누이 특징열들은 두 개의 원소로만 구성됩니다. 각 데이터 포인트 \(\mathbf{x} = (x_1, \ldots, x_D)\)가 특징을 갖든지(\(x_d=1\)) 안갖든지(\(x_d=0\)) 두개의 가능성만 갖는 자료들로 이루어집니다.
클래스 \(y=C_k\)가 주어질 때 \(d\) 번째 특징이 1이 될 확률을 \(\theta_{d,k}\)라고 하면 확률은 다음과 같이 됩니다.
다음과 같이 100개의 데이터포인트와 2개의 특징 및 2개의 클래스를 갖는 인위적인 자료를 만듭니다.
In [158]: from sklearn.datasets import make_blobs
.....: X, y = make_blobs(100, 2, centers=2, random_state=2, cluster_std=1.5)
.....:
In [160]: fig, ax = plt.subplots()
.....: ax.scatter(X[:, 0], X[:, 1], c=y, cmap='PiYG')
.....:
Out[161]: <matplotlib.collections.PathCollection at 0x156bf0eb320>
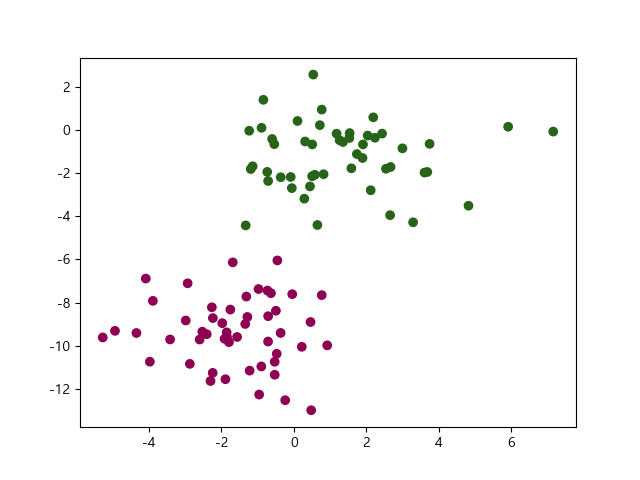
BernoulliNB 클래스를 이용해서 인스턴스를 만들어 테스트 점수를 구합니다.
In [162]: from sklearn.naive_bayes import BernoulliNB
.....: X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
.....: model = BernoulliNB(binarize=0.0)
.....: model.fit(X_train, y_train)
.....: print("테스트 점수: {}".format(model.score(X_test, y_test)))
.....:
Out[165]: BernoulliNB(alpha=1.0, binarize=0.0, class_prior=None, fit_prior=True)
테스트 점수: 0.84
다항분포(multinomial) 나이브 베이즈¶
특징 들이 일어난 횟수로 이루어진 데이터포인트들로 이루어진 데이터의 모델에 적합합니다. 예를 들어 각 특징 열들이 어떤 문장에 나타나는 단어라고 하면 데이터포인트 벡터는 각 단어들이 한 문장에 나타나는 횟수로 구성된다고 볼 수 있습니다. 아래표에서 각 행은 각 문장이 4개의 단어를 포함하는 횟수를 적은 것이고 마지막 열은 그것의 클래스를 표시한 것입니다.
| 이메일(\(X_1\)) | 사랑(\(X_2\)) | 아름다운(\(X_3\)) | 과일(\(X_4\)) | 클래스(타깃)(\(y\)) | |
| \(\mathbf{x}_1\) | 3 | 2 | 5 | 1 | 정상 |
| \(\mathbf{x}_2\) | 2 | 2 | 0 | 2 | 비정상 |
| \(\mathbf{x}_3\) | 8 | 2 | 5 | 9 | 정상 |
| \(\mathbf{x}_4\) | 6 | 0 | 5 | 1 | 비정상 |
\(x_{d,k}\)는 클래스 \(y=C_k\)일 때 \(d\)번째 특징의 값이 되고 \(\theta_{d,k}\)는 클래스 \(y=C_k\)일 때 특징 \(d\)의 확률 \(\theta_{d,k}=P(x_d \mid y=C_k)\)이 됩니다.
스팸 메일을 분류해봅니다. 웹사이트에서 다운로드를 합니다.
In [167]: url = "https://archive.ics.uci.edu/ml/machine-learning-databases/00228/smsspamcollection.zip"
.....: import urllib
.....: import os
.....:
.....: _, zip_fname = os.path.split(url)
.....: zip_path = os.path.join("data", zip_fname)
.....: if not os.path.exists(zip_path):
.....: urllib.request.urlretrieve(url, zip_path)
.....:
다운로드 받은 압축파일을 해제하여 판다스 데이터프레임으로 읽어 옵니다.
In [173]: import zipfile
.....: import pandas as pd
.....:
.....: zip_ref = zipfile.ZipFile(zip_path)
.....: with zip_ref.open(zip_ref.infolist()[0].filename) as fl:
.....: sms = pd.read_table(fl, sep='\t', header=None)
.....: sms.columns = ["v1", "v2"]
.....:
MultinomialNB 클래스를 이용해서 분류 모델을 삼고 TfidfVectorizer를 이용해서 텍스트 문장을 단어들이 얼마나 자주 등장하느냐에 따라 단어 수에 가중치를 부여한 행렬로 변환시킵니다.
TF-IDF(Term Frequency – Inverse Document Frequency) 인코딩은 단어를 갯수 그대로 카운트하지 않고 모든 문서에 공통적으로 들어있는 단어의 경우 문서 구별 능력이 떨어진다고 보아 가중치를 축소하는 방법이다. [1]
구제적으로는 문서 d(document)와 단어 t에 대해 다음과 같이 계산한다.
여기에서
- tf(d,t) : term frequency. 특정한 단어의 빈도수
- idf(t) : inverse document frequency. 특정한 단어가 들어 있는 문서의 수에 반비례하는 수
- n : 전체 문서의 수
- df(t) : 단어 t 를 가진 문서의 수
In [177]: from sklearn.naive_bayes import MultinomialNB
.....: clf = MultinomialNB()
.....: from sklearn.feature_extraction.text import TfidfVectorizer
.....: vectorizer = TfidfVectorizer()
.....:
메일을 훈련 집합과 테스트 집합으로 나눈 다음 변환된 텍스트 행렬을 이용해서 학습을 시키고 예측을 해봅니다.
In [181]: from sklearn.model_selection import train_test_split
.....: X_train, X_test, y_train, y_test = train_test_split(sms.v2, sms.v1, random_state=42)
.....: vec_text = vectorizer.fit_transform(X_train)
.....: clf.fit(vec_text, y_train)
.....:
.....: test_text = vectorizer.transform(X_test)
.....: clf.score(test_text, y_test)
.....:
.....: clf.predict(vectorizer.transform(["Please contact me as soon as possible"]))
.....:
Out[184]: MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)
Out[186]: 0.9641062455132807
Out[187]: array(['ham'], dtype='<U4')
결정 트리(Decision Tree)¶
트리 다이어그램을 그리기 위해서는 graphviz 모듈이 필요합니다. 다음과 같이 설치를 합니다.
conda install graphviz
conda install python-graphviz
In [188]: mglearn.plots.plot_animal_tree()
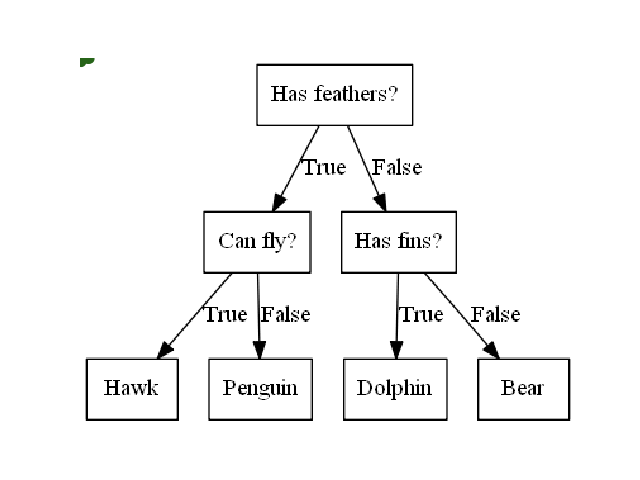
트리의 질문이나 정답을 담은 네모 상자를 노드라고 부릅니다. 마지막 노드를 리프(leaf)라고도 합니다.
다음은 두 개의 초승달을 포개어 놓은 듯한 데이터셋입니다. 2개의 클래스로 이루어져 있으면 각 클래스는 2개의 특징을 갖는 50개의 데이터포인트들로 구성됩니다.
In [189]: from sklearn.datasets import make_moons
.....: fig.clear()
.....: X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
.....: fig, ax = plt.subplots()
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
.....: ax.set_xlabel("특징 0")
.....: ax.set_ylabel("특징 1")
.....: ax.legend(["클래스 0", "클래스 1"], loc="best")
.....:
Out[193]:
[<matplotlib.lines.Line2D at 0x156bf4be208>,
<matplotlib.lines.Line2D at 0x156bf4be320>]
Out[194]: Text(0.5,0,'특징 0')
Out[195]: Text(0,0.5,'특징 1')
Out[196]: <matplotlib.legend.Legend at 0x156bf0d8908>
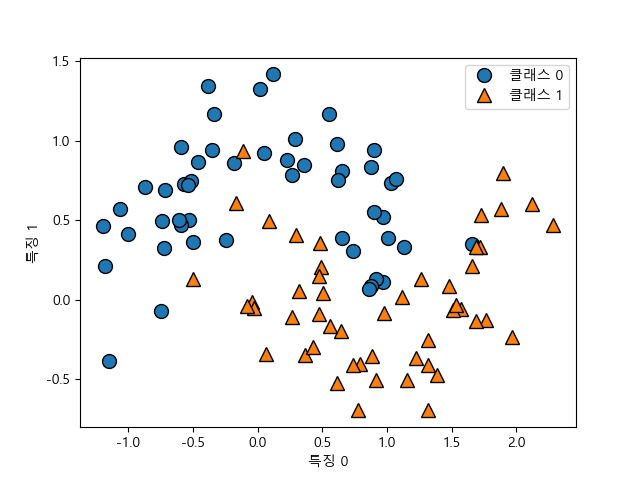
오른쪽 다이어그램에서 x[0]는 x축, x[1]은 y축을 의미합니다.
In [197]: from mglearn.plot_interactive_tree import plot_tree, tree_image
.....: fig, ax = plt.subplots(1, 2, figsize=(12, 4), subplot_kw={'xticks': (), 'yticks': ()})
.....: tree = plot_tree(X, y, max_depth=1, ax=ax[0])
.....: ax[1].imshow(tree_image(tree))
.....: ax[1].set_axis_off()
.....: fig.tight_layout()
.....:
Out[200]: <matplotlib.image.AxesImage at 0x156bc25bda0>
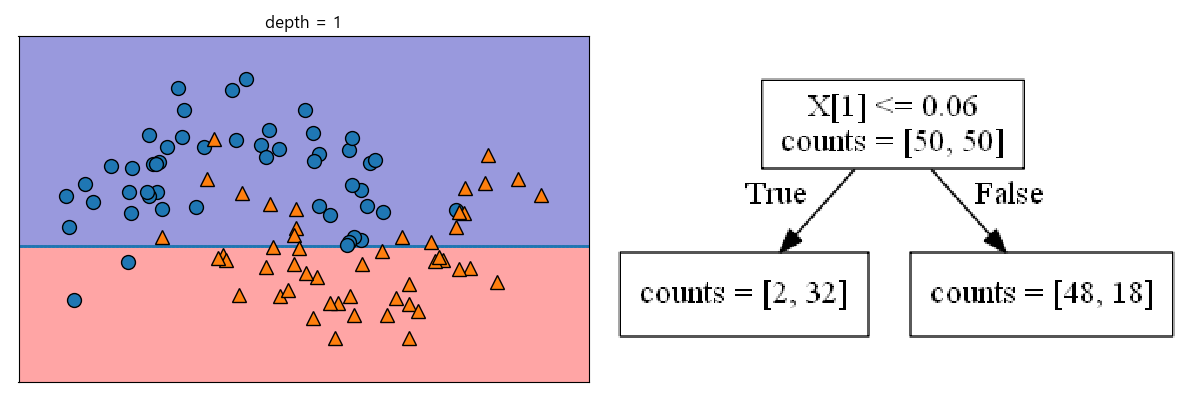
각 분할된 영역이 한 개의 타깃값(클래스가 하나)을 가질 때까지 반복됩니다. 한 종류의 클래스로만 이루어진 리프노드를 순수 노드(pure node)라고 합니다.
In [203]: fig, ax = plt.subplots(1, 2, figsize=(12, 4), subplot_kw={'xticks': (), 'yticks': ()})
.....: tree = plot_tree(X, y, max_depth=2, ax=ax[0])
.....: ax[1].imshow(tree_image(tree))
.....: ax[1].set_axis_off()
.....: fig.tight_layout()
.....:
Out[205]: <matplotlib.image.AxesImage at 0x156b8114dd8>
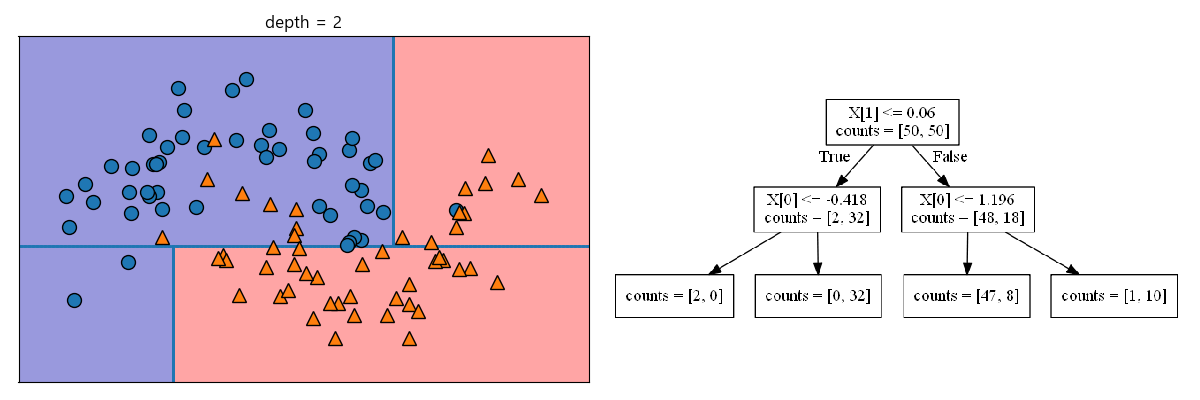
In [208]: fig, ax = plt.subplots(1, 2, figsize=(12, 4), subplot_kw={'xticks': (), 'yticks': ()})
.....: tree = plot_tree(X, y, max_depth=9, ax=ax[0])
.....: ax[1].imshow(tree_image(tree))
.....: ax[1].set_axis_off()
.....: fig.tight_layout()
.....:
Out[210]: <matplotlib.image.AxesImage at 0x156bfa46588>
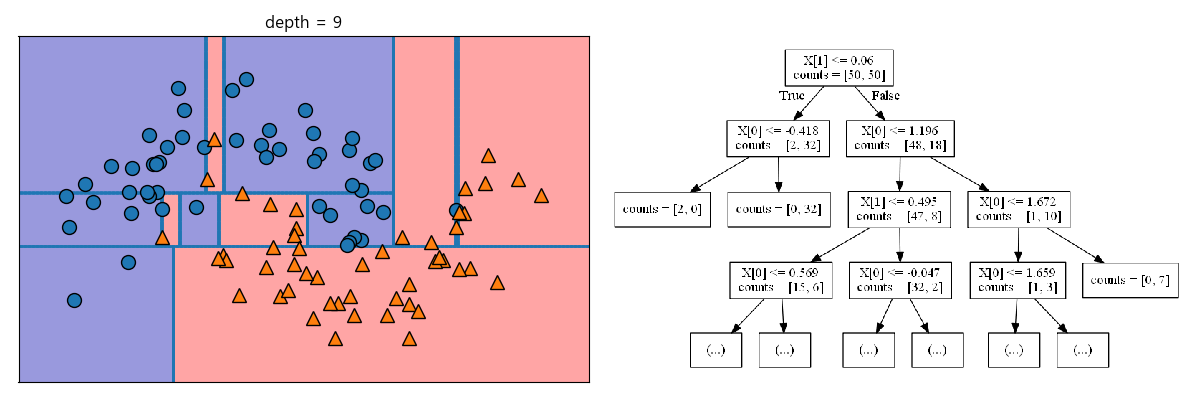
새로운 데이터 포인트에 대한 예측은 주어진 데이터 포인트가 분할된 영역들 중 어디에 속하는 가를 확인하면 됩니다. 속한 영역의 타깃값 중 가장 많은 것을 예측값으로 설정합니다. 회귀 문제에도 마찬가지 방법으로 리프 노드를 찾은 후 훈련 데이터 평균값이 예측값이 됩니다.
결정 트리의 복잡도 제어¶
모든 리프 노드가 순수 노드가 될 때까지 진행하면 훈련 집합에 100% 정확하게 맞는 것이되어 과대적합이 됩니다. 과대적합을 맞는 방법으로는 트리 생성을 적당히 중단하는 방법(사전 가지치기; pre-pruning)과 트리를 만든 후 데이터 포인트가 적은 노드를 삭제하는 방법(사후 가지치기; post-pruning)이 있습니다.
scikit-learn의 결정 트리는 DecisionTreeRegressor와 DecisionTreeClassifier에 구현되어 있으며 사전 가지치기만 지원합니다.
유방암 데이터셋을 이용해서 사전 가지치기 효과에 대해서 살펴보겠습니다.
In [213]: from sklearn.tree import DecisionTreeClassifier
.....: cancer = load_breast_cancer()
.....: X_train, X_test, y_train, y_test = train_test_split(\
.....: cancer.data, cancer.target, stratify=cancer.target, random_state=42)
.....: tree = DecisionTreeClassifier(random_state=0)
.....: tree.fit(X_train, y_train)
.....: print("훈련 집합 정확도: {:.3f}".format(tree.score(X_train, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(tree.score(X_test, y_test)))
.....:
Out[217]:
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=0,
splitter='best')
훈련 집합 정확도: 1.000
테스트 집합 정확도: 0.937
리프 노드가 순수 노드들로만 이루어져 있기 때문에 훈련 집합의 정확도가 100%인 것을 알 수 있습니다. max_depth 옵션을 이용해서 트리의 깊이를 최대 4까지로만 제한해서 사전 가지치기 효과를 얻어봅니다.
In [220]: tree = DecisionTreeClassifier(max_depth=4, random_state=0)
.....: tree.fit(X_train, y_train)
.....: print("훈련 집합 정확도: {:.3f}".format(tree.score(X_train, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(tree.score(X_test, y_test)))
.....:
Out[221]:
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=4,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=0,
splitter='best')
훈련 집합 정확도: 0.988
테스트 집합 정확도: 0.951
결정 트리 분석¶
export_graphviz 함수를 이용해 트리를 텍스트 형식의 .dot 파일을 만들 수 있습니다.
In [224]: from sklearn.tree import export_graphviz
.....: export_graphviz(tree, out_file="tree.dot", class_names=["악성", "양성"],\
.....: feature_names=cancer.feature_names, impurity=False, filled=True)
.....:
이 파일을 graphviz 모듈을 이용해서 시각화할 수 있습니다.
In [226]: import graphviz
.....: with open("tree.dot", encoding='utf-8') as f:
.....: dot_graph = f.read()
.....: gv_src = graphviz.Source(dot_graph, filename='_static/images/tree_gv', format='svg')
.....: gv_src.render()
.....:
Out[227]: '_static/images/tree_gv.svg'
트리의 특징 중요도¶
트리를 만드는 결정에 각 특징이 얼마나 중요하게 기여했는지를 알아보는 특징 중요도(feature importance)를 살펴봅니다. 이 값은 0과 1 사이의 수로 0은 전혀 사용되지 않았다는 것이고 1은 완벽하게 사용되었다는 것을 의미합니다. 전체 합하면 1입니다.
In [228]: n_features = cancer.data.shape[1]
.....: plt.clf()
.....: plt.barh(range(n_features), tree.feature_importances_, align='center');
.....: plt.yticks(np.arange(n_features), cancer.feature_names);
.....: plt.xlabel("특징 중요도");
.....: plt.ylabel("특징");
.....: plt.ylim(-1, n_features);
.....: plt.tight_layout()
.....:
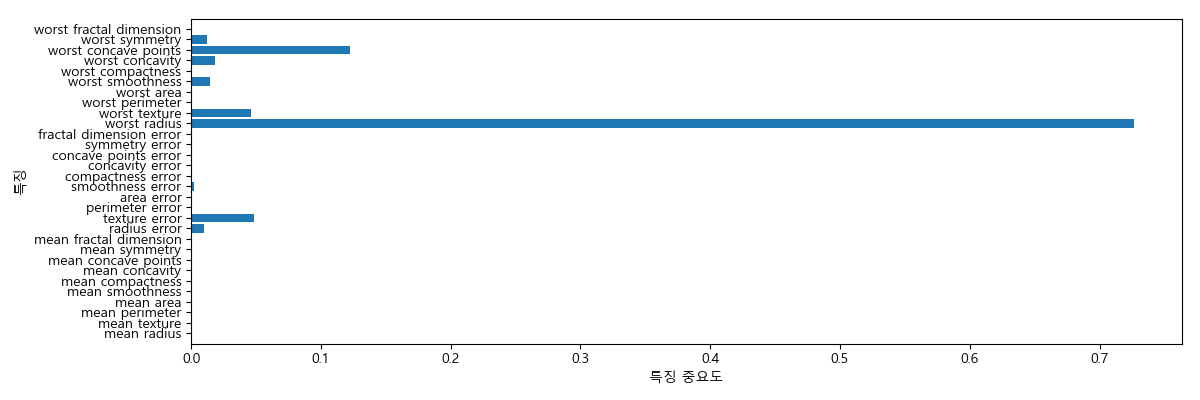
결정 트리 앙상블¶
앙상블(ensemble)이란 여러 머신러닝 모델들을 연결하여 더 강력한 모델을 만드는 기법을 말합니다. 여기서는 랜덤 포레스트(random forest)와 그래디언트 부스팅(gradient boosting) 앙상블 모델에 대해서만 살펴보겠습니다.
랜덤 포레스트¶
결정 트리는 비교적 예측을 잘 할 수 있지만 데이터의 일부에 과대적합하는 경향있습니다. 랜덤 포레스트는 서로 다른 방향으로 과대적합된 트리를 많이 만들어 그 결과를 평균냄으로 과대적합된 양을 줄이는 방향으로 모델을 만들어 나갑니다. 이것을 구현하려면 각각의 결정 트리들이 타깃 예측을 잘해야 하고 다른 트리와 구별되게 만들어야 합니다.
트리를 랜덤하게 만드는 방법으로 트리를 만들 때 데이터 포인트를 무작위로 선택하는 방법과 분할 테스트에 사용되는 특징을 미리 무작위로 선택 지정하는 방법입니다.
랜덤 포레스트 구축¶
랜덤 포레스트 모델은 RandomForestRegressor와 RandomForestClassifier를 이용해 만들 수 있고 트리의 갯수(n_estimators)를 정해야 합니다.
트리를 만들기위해 데이터의 부트스트랩 표본(bootstrap sample)을 생성합니다. 즉, 주어진 데이터 포인트 갯수만큼의 표본을 주어진 데이터에서 반복 중복 추출하여 얻어진 표본을 사용합니다.
이러한 부트스트랩 표본을 이용하여 결정 트리를 만듭니다. 앞에서 본 결정 트리 알고리즘은 각 노드에서 전체 특징을 대상으로 최선의 테스트를 찾는 것이었지만 랜덤 포레스트 알고리즘은 각 노드에서 후보 특징을 무작위로 선택한 후 이 후보들 중에서 최선의 테스트를 찾습니다. 몇 개의 특징을 선택할 지는 max_features 옵션을 통해 조정할 수 있습니다.
후보 특징을 고르는 것은 매 노드마다 반복되므로 각 노드는 다른 후보 특징들을 사용하여 테스트를 만들게 됩니다.
랜덤 포레스트를 이용하여 예측을 할 때는 모든 트리의 예측을 만듭니다. 회귀의 경우는 이 예측들을 평균하여 최종 예측을 하고 분류의 경우는 트리들이 예측한 확률들을 평균내어 가장 높은 확률을 가진 클래스가 예측값이 됩니다.
랜덤 포레스트 분석¶
In [236]: from sklearn.ensemble import RandomForestClassifier
.....: from sklearn.datasets import make_moons
.....:
.....: X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
.....: X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
.....: forest = RandomForestClassifier(n_estimators=5, random_state=2)
.....: forest.fit(X_train, y_train)
.....:
Out[241]:
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=5, n_jobs=1,
oob_score=False, random_state=2, verbose=0, warm_start=False)
In [242]: fig, axes = plt.subplots(2, 3, figsize=(20, 10))
.....: for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)):
.....: ax.set_title("트리 {}".format(i))
.....: mglearn.plots.plot_tree_partition(X, y, tree, ax=ax)
.....:
.....: mglearn.plots.plot_2d_separator(forest, X, fill=True, ax=axes[-1, -1], alpha=.4)
.....: axes[-1, -1].set_title("랜덤 포레스트")
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
.....: fig.tight_layout()
.....:
Out[245]: Text(0.5,1,'랜덤 포레스트')
Out[246]:
[<matplotlib.lines.Line2D at 0x156c00072e8>,
<matplotlib.lines.Line2D at 0x156c003ee10>]
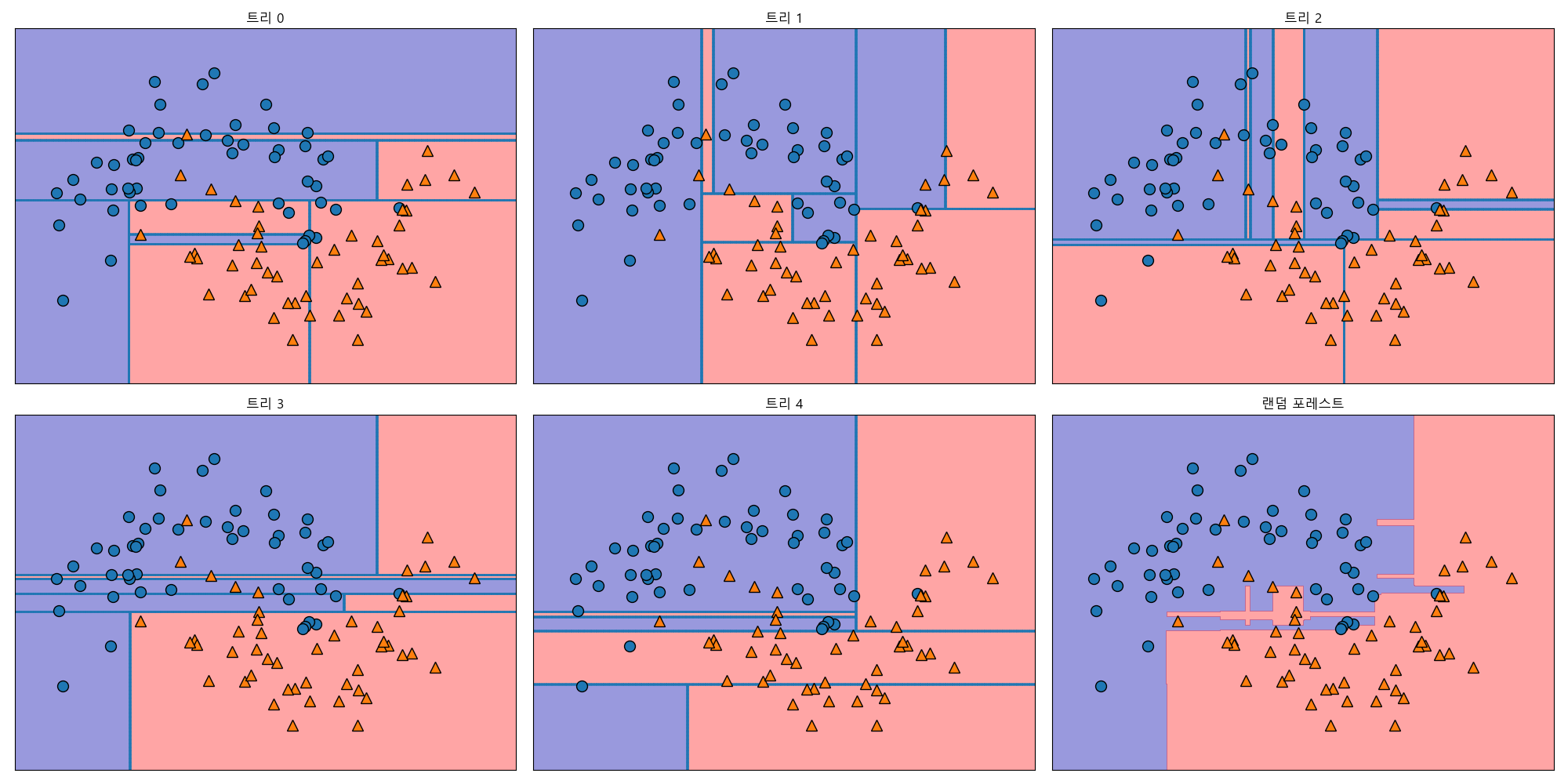
유방암 데이터셋에 100개의 트리로 이루어진 랜덤 포레스트를 적용해봅니다.
In [248]: X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)
.....: forest = RandomForestClassifier(n_estimators=100, random_state=0)
.....: forest.fit(X_train, y_train)
.....: print("훈련 집합 정확도: {:.3f}".format(forest.score(X_train, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(forest.score(X_test, y_test)))
.....:
Out[250]:
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=1,
oob_score=False, random_state=0, verbose=0, warm_start=False)
훈련 집합 정확도: 1.000
테스트 집합 정확도: 0.972
그래디언트 부스팅 회귀 트리¶
그래디언트 부스팅은 랜덤 포레스트와는 달리 여러 개의 얕은 트리(weak tree)를 만들어 순차적으로 이전 트리의 오차를 줄이는 방식으로 동작을 합니다. 일반적으로 트리의 깊이는 5개 이하로 잡아 간단한 모델을 만들어 빠른 예측을 가능케합니다.
그래디언트 부스팅에서 중요한 매개변수로 learning_rate를 들 수 있습니다. 이전 트리의 오차를 얼마나 강하게 보정을 할 지를 결정합니다. n_estimators를 이용해서 트리의 갯수를 지정할 수 있습니다.
유방암 데이터셋을 이용하여 GradientBoostingClassifier를 사용해봅니다. 기본값은 max_depth=3, n_estimators=100, learning_rate=0.1입니다.
In [253]: from sklearn.ensemble import GradientBoostingClassifier
.....:
.....: X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)
.....: gbrt = GradientBoostingClassifier(random_state=0)
.....: gbrt.fit(X_train, y_train)
.....: print("훈련 집합 정확도: {:.3f}".format(gbrt.score(X_train, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(gbrt.score(X_test, y_test)))
.....:
Out[256]:
GradientBoostingClassifier(criterion='friedman_mse', init=None,
learning_rate=0.1, loss='deviance', max_depth=3,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
presort='auto', random_state=0, subsample=1.0, verbose=0,
warm_start=False)
훈련 집합 정확도: 1.000
테스트 집합 정확도: 0.958
과대적합을 막기위해서 트리의 최대 깊이를 줄이거나 학습률을 낮출 수 있습니다.
In [259]: gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
.....: gbrt.fit(X_train, y_train)
.....:
.....: print("훈련 집합 정확도: {:.3f}".format(gbrt.score(X_train, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(gbrt.score(X_test, y_test)))
.....:
Out[260]:
GradientBoostingClassifier(criterion='friedman_mse', init=None,
learning_rate=0.1, loss='deviance', max_depth=1,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
presort='auto', random_state=0, subsample=1.0, verbose=0,
warm_start=False)
훈련 집합 정확도: 0.991
테스트 집합 정확도: 0.972
In [263]: gbrt = GradientBoostingClassifier(random_state=0, learning_rate=0.01)
.....: gbrt.fit(X_train, y_train)
.....:
.....: print("훈련 집합 정확도: {:.3f}".format(gbrt.score(X_train, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(gbrt.score(X_test, y_test)))
.....:
Out[264]:
GradientBoostingClassifier(criterion='friedman_mse', init=None,
learning_rate=0.01, loss='deviance', max_depth=3,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
presort='auto', random_state=0, subsample=1.0, verbose=0,
warm_start=False)
훈련 집합 정확도: 0.988
테스트 집합 정확도: 0.965
특성의 중요도를 시각화해봅니다.
In [267]: fig.clear()
.....: def plot_feature_importance_cancer(model):
.....: n_features = cancer.data.shape[1]
.....: plt.barh(range(n_features), model.feature_importances_, align='center')
.....: plt.yticks(np.arange(n_features), cancer.feature_names)
.....: plt.xlabel("특성 중요도")
.....: plt.ylabel("특성")
.....: plt.ylim(-1, n_features)
.....: plt.tight_layout()
.....: gbrt = GradientBoostingClassifier(random_state=0, learning_rate=0.01)
.....: gbrt.fit(X_train, y_train)
.....:
.....: plot_feature_importance_cancer(gbrt)
.....:
Out[268]:
GradientBoostingClassifier(criterion='friedman_mse', init=None,
learning_rate=0.01, loss='deviance', max_depth=3,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
presort='auto', random_state=0, subsample=1.0, verbose=0,
warm_start=False)
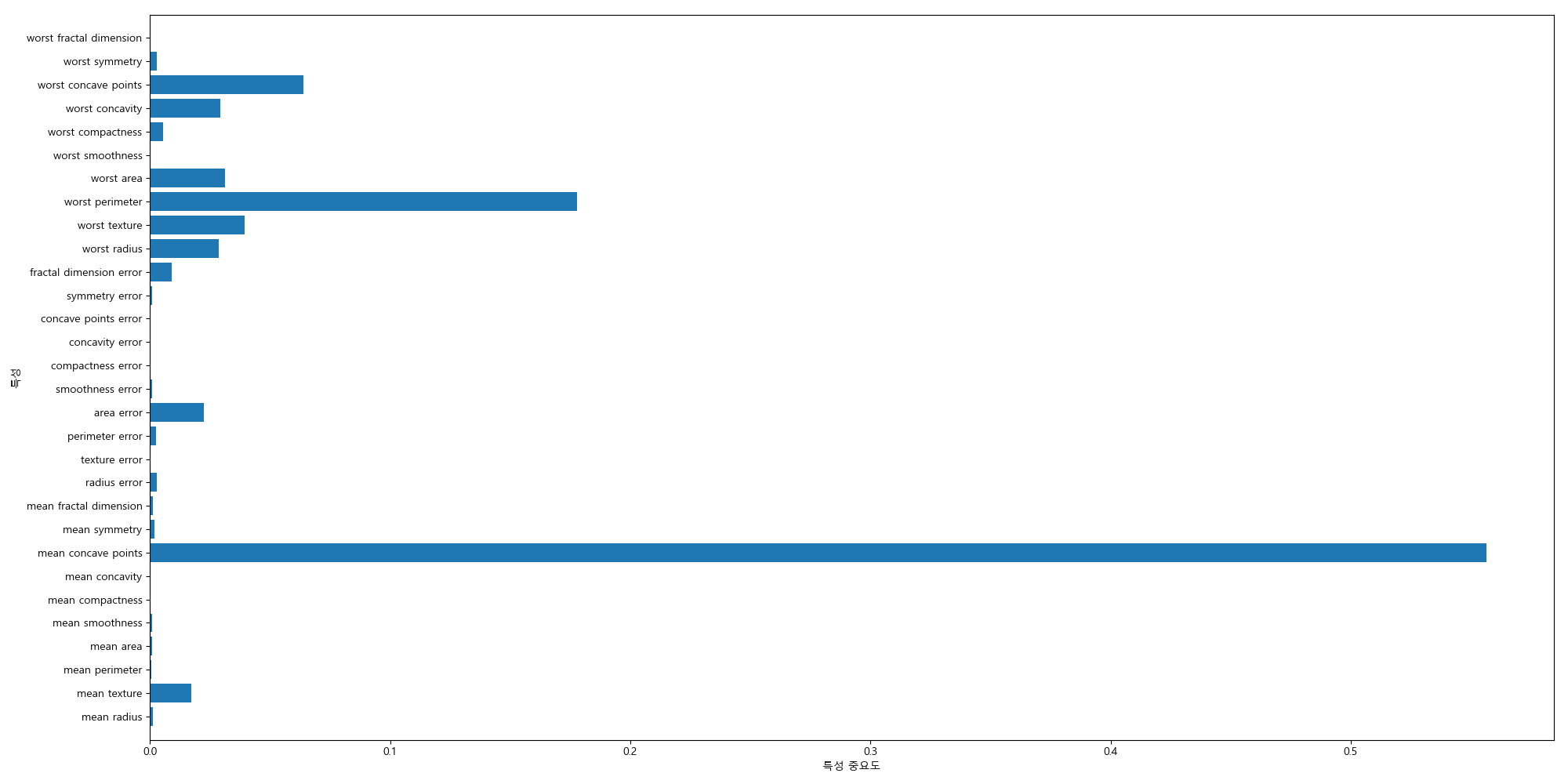
커널 서포트 벡터 머신¶
선형 서포트 벡터 머신에서는 초평면(hyperplane)을 이용해서 분류를 했는데 커널 서포트 벡터 머신은 비선형 함수를 커널로 사용함으로 더 복잡한 모델을 만들수 있도록 확장한 것입니다.
선형 모델과 비선형 특징¶
선형 모델을 유연하게 만드는 방법으로 특징들의 연산을 통해 새로운 특징을 만들어 확장하는 방법이 있습니다.
다음은 인위적인 데이터셋을 만들어 사용해보겠습니다. 100개의 2차원 데이터포인트와 4개의 그룹으로 나뉘어진 데이터입니다. 클래스는 2개로 지정해서 사용합니다.
In [270]: X, y = make_blobs(centers=4, random_state=8)
.....: y = y % 2
.....:
.....: plt.cla()
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y);
.....: plt.xlabel("특성 0");
.....: plt.ylabel("특성 1");
.....:
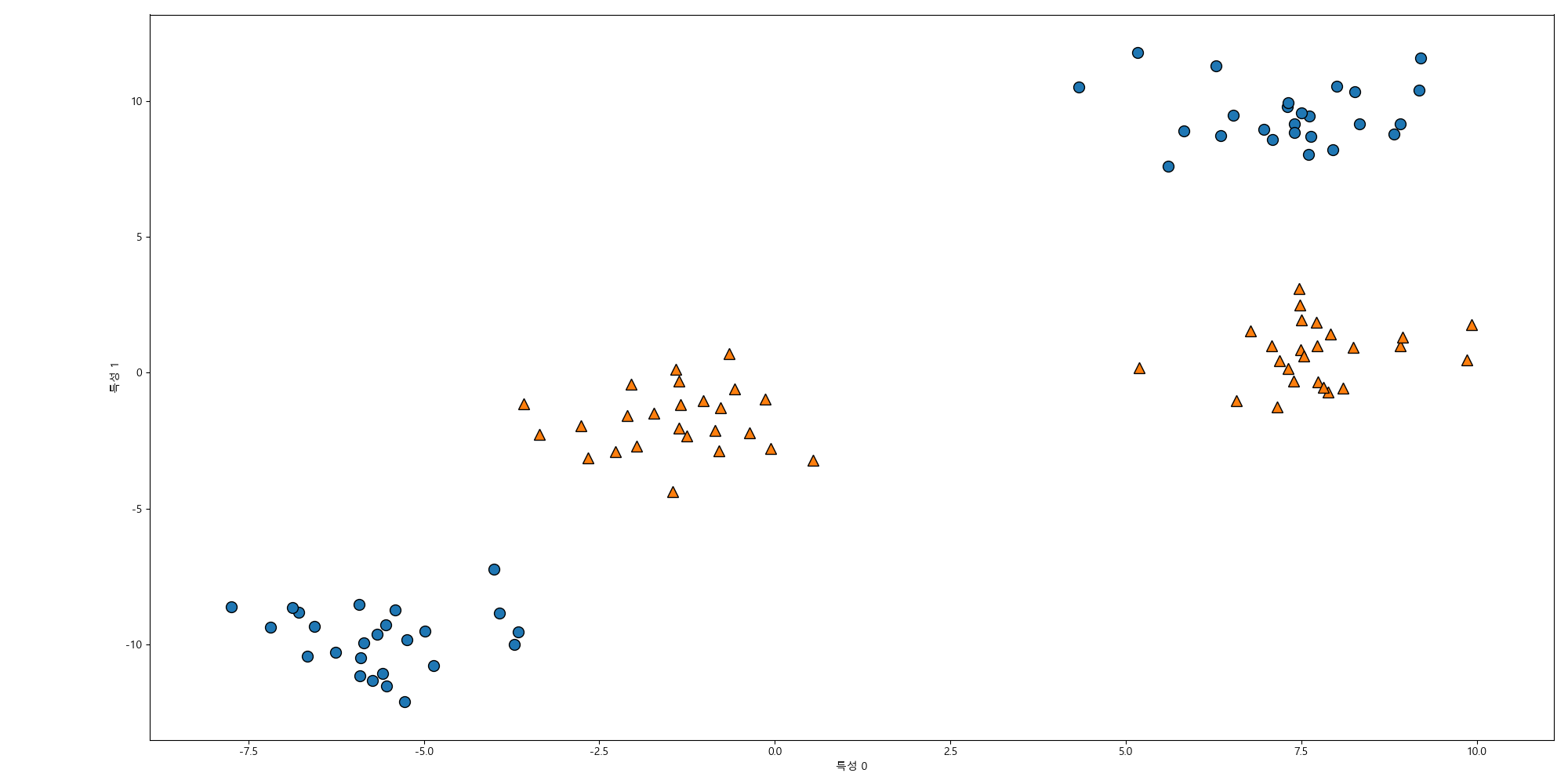
선형 모델은 직선으로 데이터를 분류하려고 하기때문에 이런 데이터셋에는 잘 작동하지 않습니다.
In [276]: from sklearn.svm import LinearSVC
.....: lin_svm = LinearSVC().fit(X, y)
.....:
.....: plt.cla()
.....: mglearn.plots.plot_2d_separator(lin_svm, X);
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y);
.....: plt.xlabel("특성 0");
.....: plt.ylabel("특성 1");
.....:
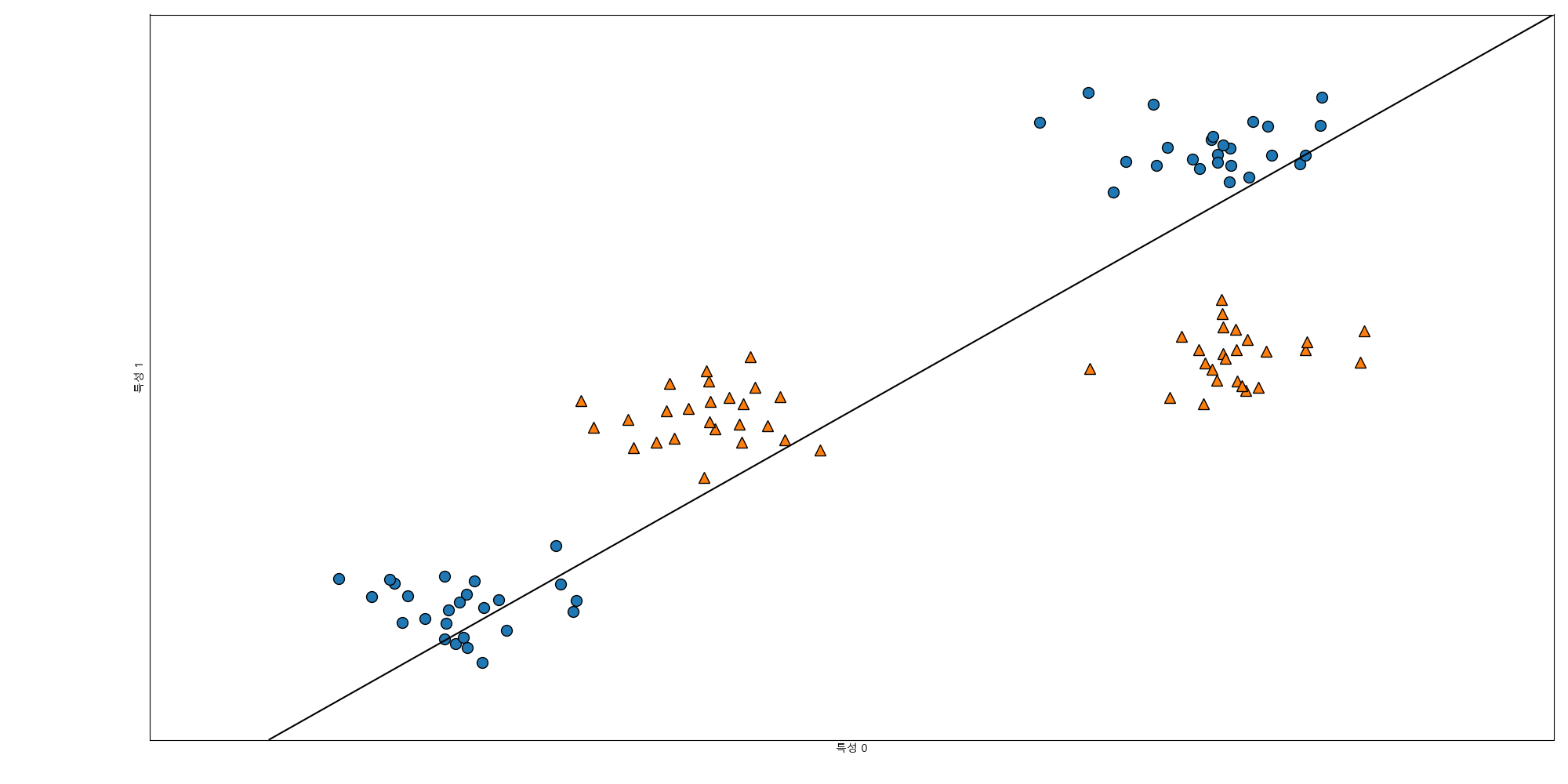
두번째 특징을 제곱해서 3차원 특징으로 확장을 해보고 산점도를 그려봅니다.
In [283]: X_new = np.hstack([X, X[:, 1:] ** 2]) # 특징열 추가
.....:
.....: from mpl_toolkits.mplot3d import Axes3D, axes3d
.....: plt.cla()
.....: figure = plt.gcf()
.....: ax = Axes3D(figure, elev=-152, azim=-26)
.....:
.....: mask = y == 0
.....: ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b', cmap=mglearn.cm2, s=60, edgecolor='k'); # 클래스 0(즉, y == 0)
.....: ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], ;c='r', marker='^', cmap=mglearn.cm2, s=60, edgecolor='k') # 클래스 1
.....: ax.set_xlabel("특성 0");
.....: ax.set_ylabel("특성 1");
.....: ax.set_zlabel("특성1 ** 2");
.....:
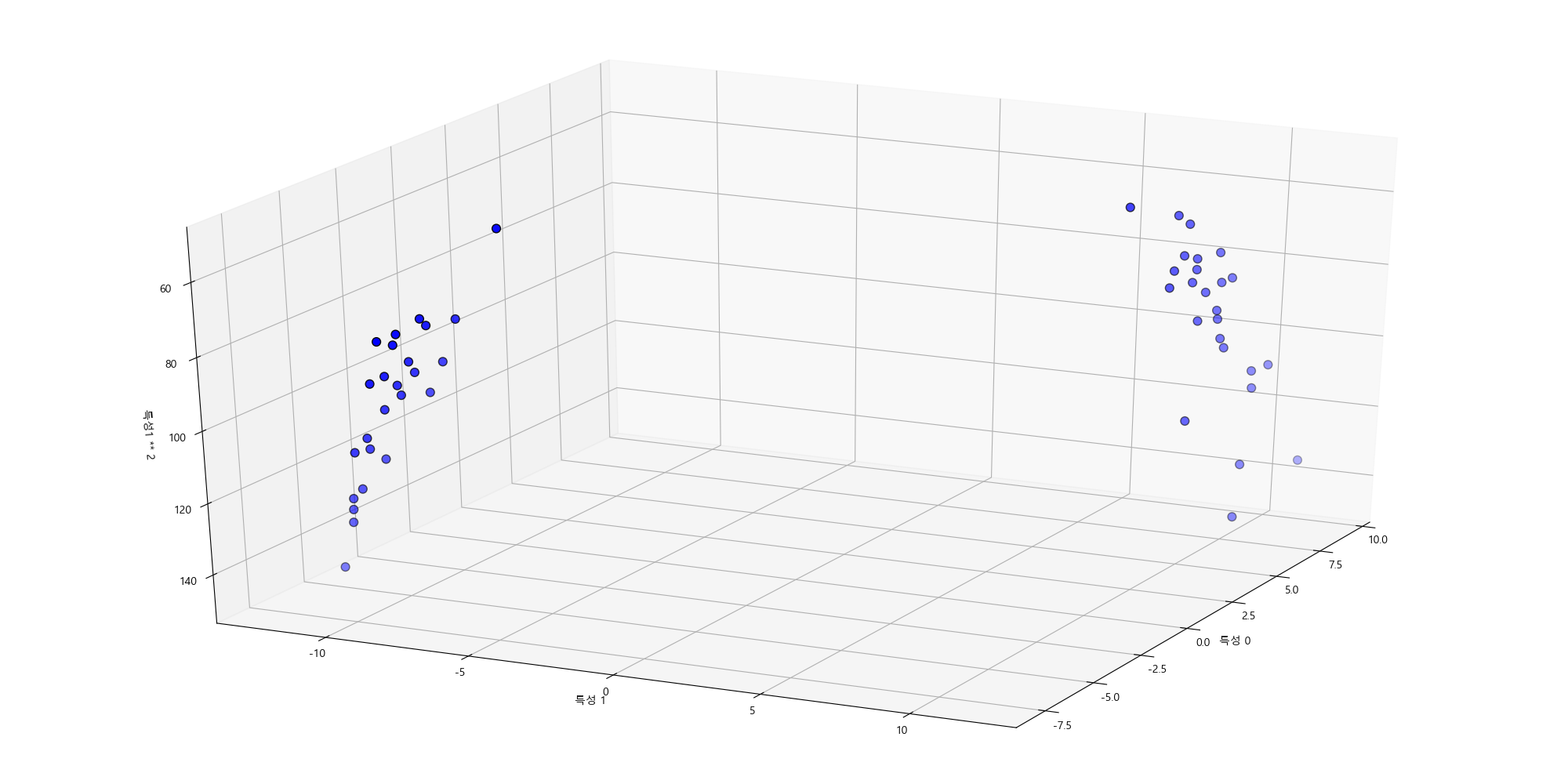
새로운 데이터셋에서는 선형 모델과 3차원 공간의 평면을 이용해서 두 클래스를 분류할 수 있습니다.
In [294]: lin_svm_3d = LinearSVC().fit(X_new, y)
.....: coef, intercept = lin_svm_3d.coef_.ravel(), lin_svm_3d.intercept_
.....: plt.cla()
.....: figure = plt.gcf()
.....: ax = Axes3D(figure, elev=-152, azim=-26)
.....: xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
.....: yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
.....:
.....: XX, YY = np.meshgrid(xx, yy)
.....: ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
.....: ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3);
.....: mask = y == 0
.....: ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b', cmap=mglearn.cm2, s=60, edgecolor='k');
.....: ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^', cmap=mglearn.cm2, s=60, edgecolor='k');
.....: ax.set_xlabel("특성 0");
.....: ax.set_ylabel("특성 1");
.....: ax.set_zlabel("특성1 ** 2");
.....:
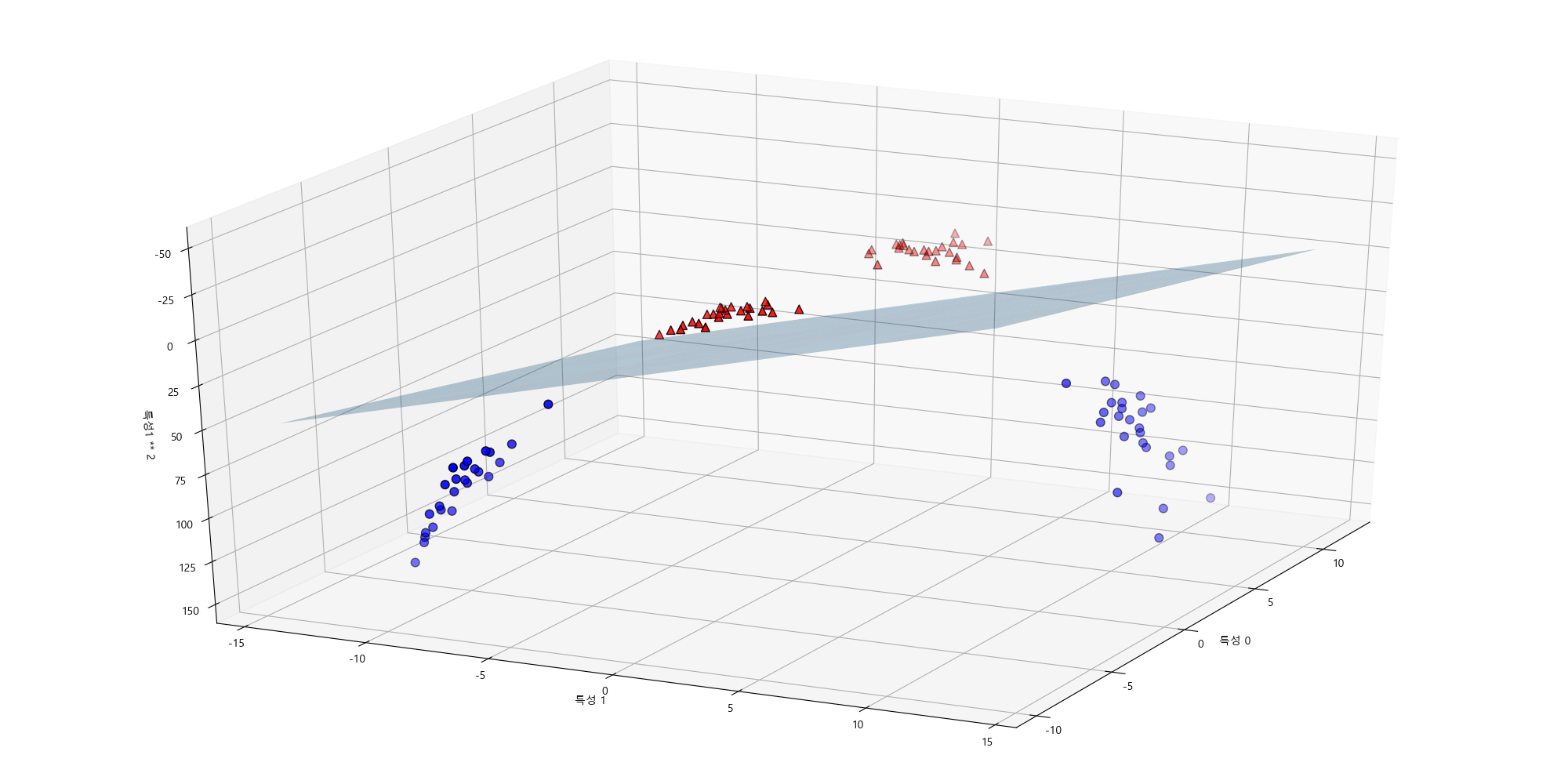
원래 특징 차원으로 투영해보면 평면은 타원으로 보이는 것을 확인할 수 있습니다.
In [310]: ZZ = YY ** 2
.....: dec = lin_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()])
.....: plt.clf()
.....: plt.cla()
.....: plt.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()], cmap=mglearn.cm2, alpha=0.5);
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y);
.....: plt.xlabel("특성 0");
.....: plt.ylabel("특성 1");
.....:
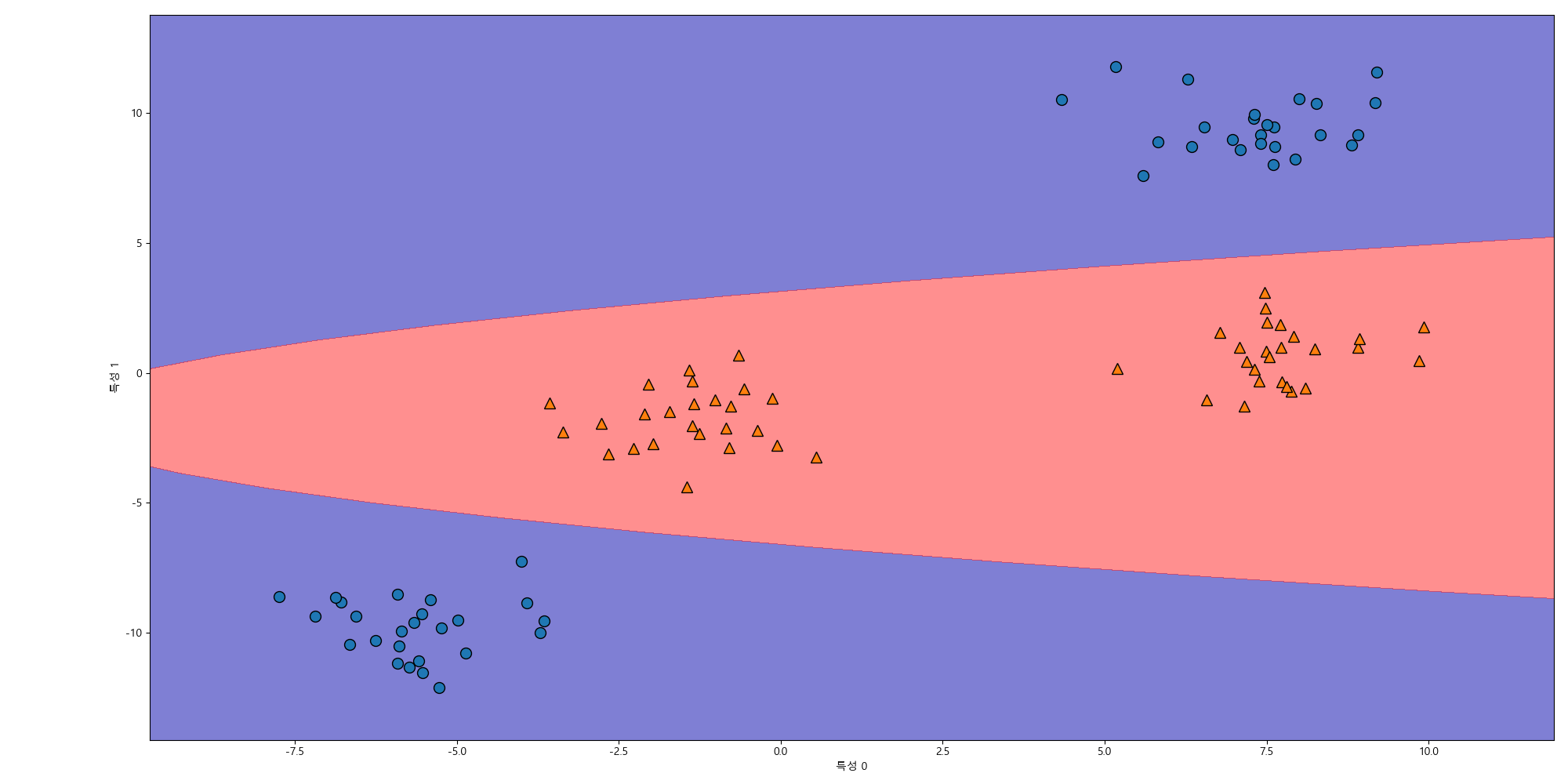
decision_function은 데이터포인트들과 초평면과의 부호가 있는 거리에 해당되는 신뢰점수(confidence score)를 반환합니다.
SVM 이해하기¶
훈련 집합을 이용해서 학습을 하면서 클래스 사이의 경계를 만드는 데이터 포인트를 찾게 됩니다. 이런 데이터 포인트를 서포트 벡터(support vector)라 합니다.
목적함수는 다음과 같이 쓸 수 있습니다.
여기서 \(a_i\)는 라그랑지 승수(Lagrange multiplier)입니다. 이 최적화 문제를 풀어 \(w, w_0, a\)를 구하면 판별함수를 얻을 수 있습니다.
서포트 벡터 머신의 목적함수의 듀얼(dual)은 다음과 같습니다.
예측 모델은 다음과 같습니다.
목적함수와 예측 모델을 기저 변환 함수 \(\phi(x)\)를 이용해서 표현하면 다음과 같습니다.
변환된 기저 함수들의 내적을 커널(kernel)이라고 합니다.
목적함수와 예측모델을 커널로 표현하면 다음과 같습니다.
주로 사용하는 커널로는 다항(polynomial) 함수, 가우시안(Gaussian) 또는 RBF(Radial Basis Function) 함수, 시그모이드(sigmoid) 함수등이 있습니다.
- 다항 커널
- 가우시안(Gaussian) 커널
- 시그모이드 커널
두 개의 클래스를 가진 2차원 데이터셋에 대한 가우시안 커널 서포트 벡터 머신을 학습시킨 결과를 그래프로 그려봅니다.
In [318]: from sklearn.svm import SVC
.....: X, y = mglearn.tools.make_handcrafted_dataset()
.....: svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
.....: plt.clf()
.....: plt.figure(figsize=(10, 8))
.....: mglearn.plots.plot_2d_separator(svm, X, eps=0.5);
.....: mglearn.discrete_scatter(X[:, 0], X[:, 1], y);
.....:
.....: sv = svm.support_vectors_
.....:
.....: sv_labels = svm.dual_coef_.ravel() > 0
.....: mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_labels, s=15, markeredgewidth=3);
.....: plt.xlabel("특성 0");
.....: plt.ylabel("특성 1");
.....:
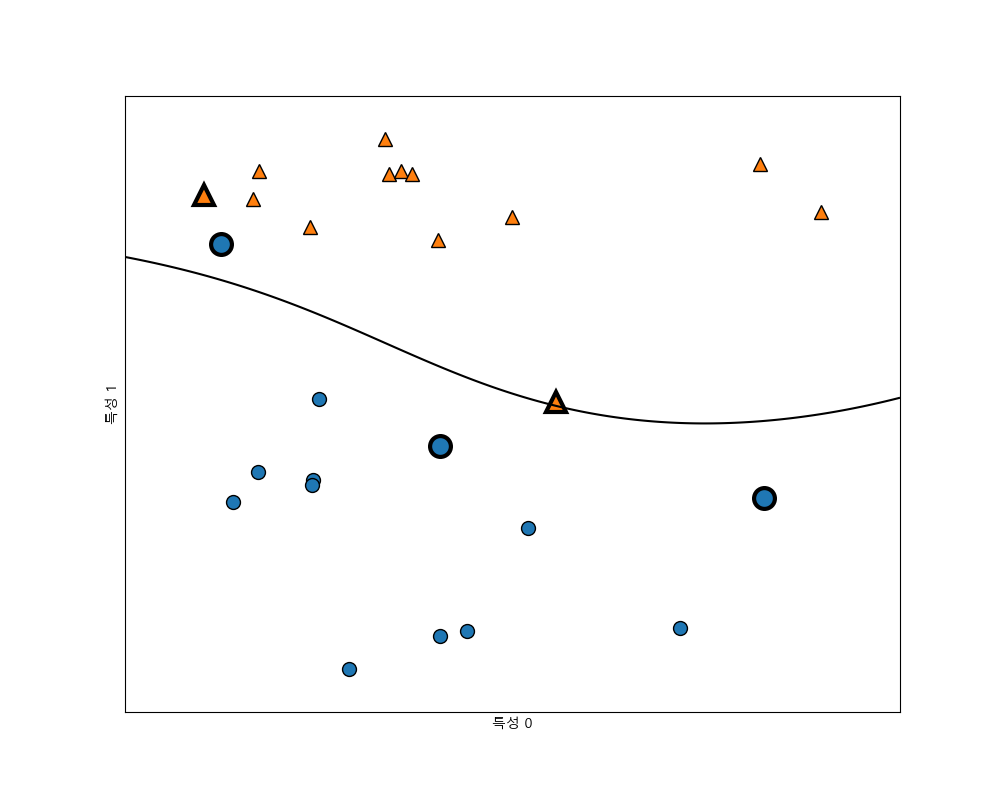
SVM 매개변수¶
감마(\(\gamma\)) 매개변수는 가우시안 커널 폭의 역수로서 작으면 넓은 영역에 걸쳐 영향을 미치고 크면 적은 영역에 영향을 미칩니다. C 매개변수는 선형모델에서 사용한 것과 비슷한 규제 매개변수입니다. 이 매개변수는 각 포인트의 중요도(dual_coef_)를 제한합니다.
이 매개변수들을 다르게 적용했을 때 어떻게 변경되는 살펴봅니다.
In [330]: fig, axes = plt.subplots(3, 3, figsize=(15, 10))
.....:
.....: for ax, C in zip(axes, [-1, 0, 3]):
.....: for a, gamma in zip(ax, range(-1, 2)):
.....: mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a)
.....:
.....: axes[0, 0].legend(["클래스 0", "클래스 1", "클래스 0 서포트 벡터", "클래스 1 서포트 벡터"], ncol=4, loc=(0.9, 1.2));
.....:
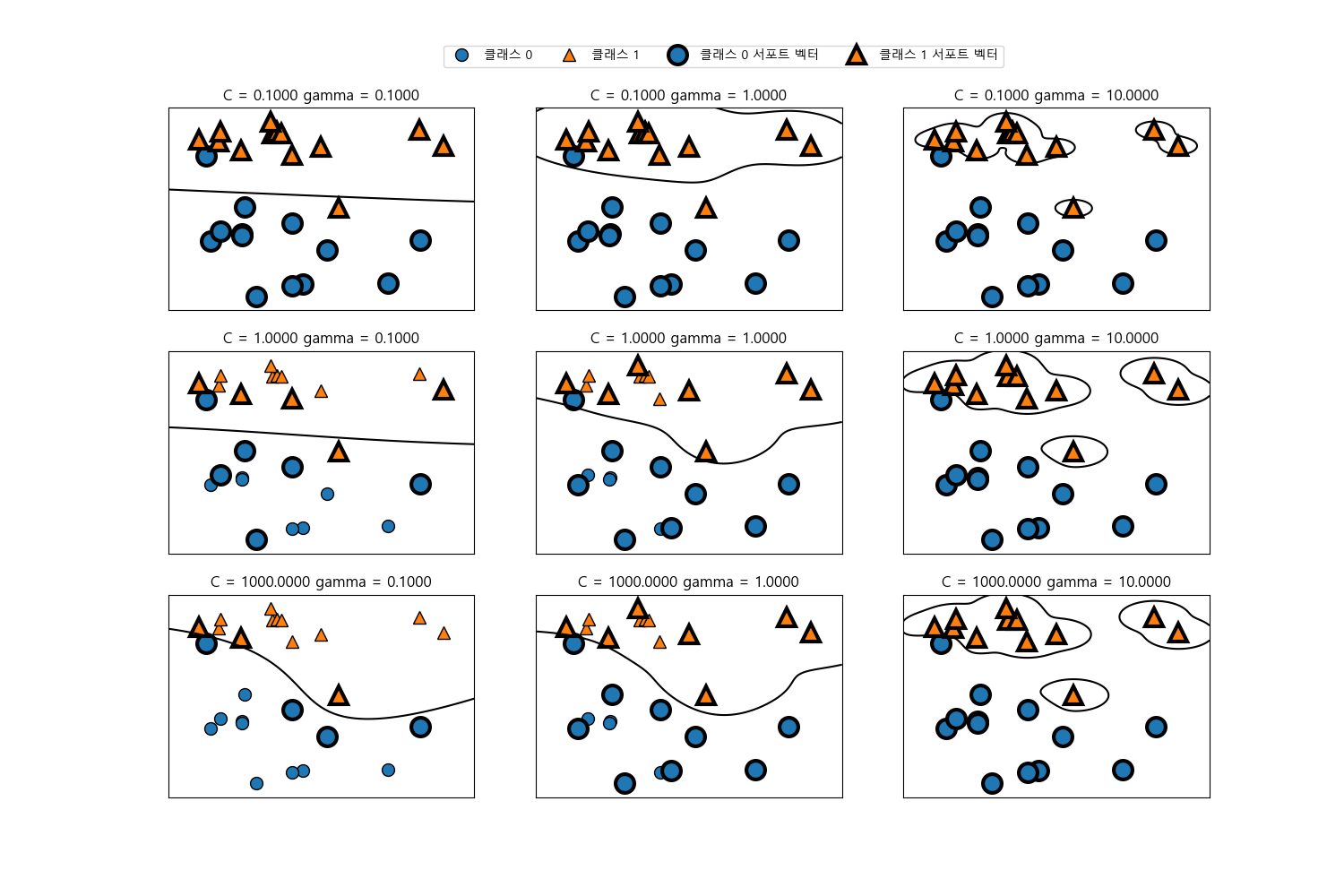
가우시안 커널 서포트 벡터 머신을 유방암 데이터셋에 적용해봅니다.
In [333]: X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)
.....:
.....: svc = SVC()
.....: svc.fit(X_train, y_train)
.....:
.....: print("훈련 집합 정확도: {:.3f}".format(svc.score(X_train, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(svc.score(X_test, y_test)))
.....:
Out[335]:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
훈련 집합 정확도: 1.000
테스트 집합 정확도: 0.629
훈련 집합에는 완벽한 점수를 냈지만 테스트 집합에는 낮은 점수를 낸 것으로보아 과대적합이 된 것을 알 수 있습니다. SVM은 매개변수 설정과 데이터 스케일에 매우 민감해서 특징의 범위를 일정하게 맞추어야 합니다.
각 특징의 최솟값과 최대값을 로그 스케일로 나타내봅니다.
In [338]: plt.clf()
.....: plt.figure(figsize=(10, 8));
.....: plt.boxplot(X_train, manage_xticks=False);
.....: plt.yscale("symlog");
.....: plt.xlabel("특성 목록");
.....: plt.ylabel("특성 크기");
.....:
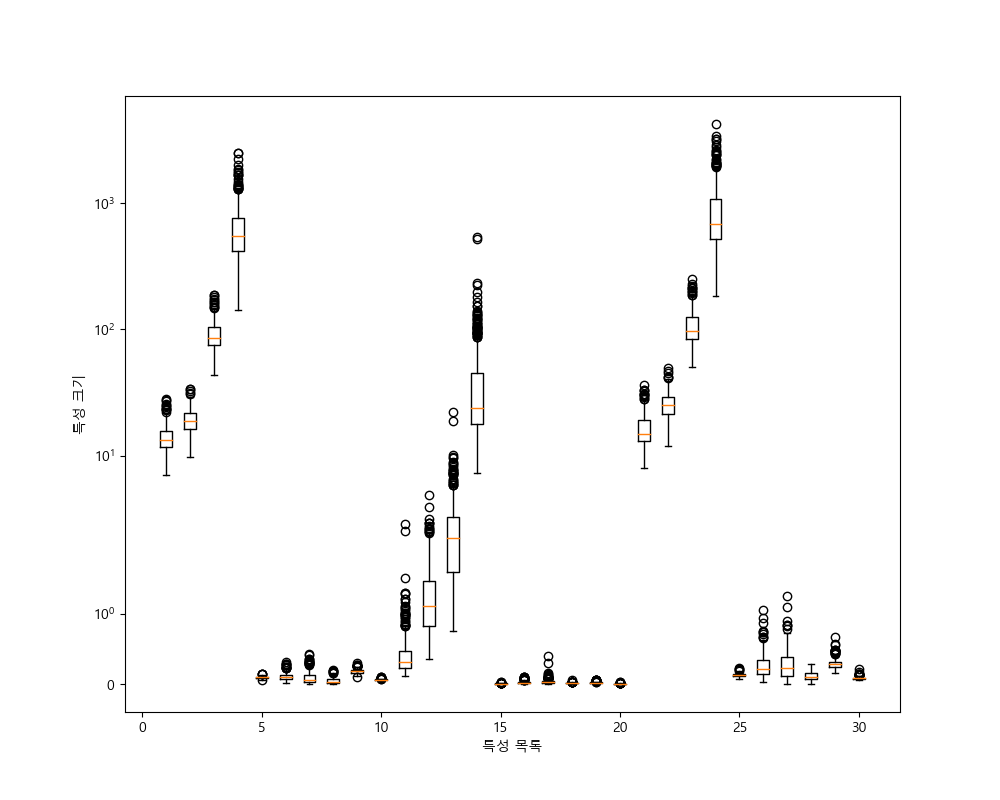
SVM 데이터 전처리¶
특징의 범위가 비슷해지도록 조정하는 방법에 대해서 다룹니다. sklearn.preprocessing의 MinMaxScaler() 함수를 이용해도 되지만 직접 만들어서 사용해봅니다.
In [344]: min_on_training = X_train.min(axis=0)
.....: range_on_training = (X_train - min_on_training).max(axis=0)
.....:
.....: X_train_scaled = (X_train - min_on_training) / range_on_training
.....: print("특징별 최솟값\n{}".format(X_train_scaled.min(axis=0)))
.....: print("특징별 최댓값\n{}".format(X_train_scaled.max(axis=0)))
.....:
특징별 최솟값
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.]
특징별 최댓값
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.]
In [349]: X_test_scaled = (X_test - min_on_training) / range_on_training
.....: svc = SVC()
.....: svc.fit(X_train_scaled, y_train)
.....:
.....: print("훈련 집합 정확도: {:.3f}".format(svc.score(X_train_scaled, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(svc.score(X_test_scaled, y_test)))
.....:
Out[351]:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
훈련 집합 정확도: 0.948
테스트 집합 정확도: 0.951
스케일을 조정한 결과 정확도가 좋아진 것을 확인할 수 있습니다. 여기서 C의 값을 증가시켜 좀 더 복잡한 모델을 만들어봅니다.
In [354]: svc = SVC(C=1000)
.....: svc.fit(X_train_scaled, y_train)
.....: print("훈련 집합 정확도: {:.3f}".format(svc.score(X_train_scaled, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(svc.score(X_test_scaled, y_test)))
.....:
Out[355]:
SVC(C=1000, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
훈련 집합 정확도: 0.988
테스트 집합 정확도: 0.972
신경망(Neural Network)¶
신경망은 다음과 같이 분류를 할 수 있습니다.
- 전방(feed-forward) 신경망과 순환(recurrent) 신경망: 전방 신경망은 모든 계산이 왼쪽에서 오른쪽으로 진행되는 반면 순환 신경망은 오른쪽에서 왼쪽으로 진행되는 피드백 계산이 포함됩니다. 다층 퍼셉트론(Multilayer Perceptron)과 컨볼루션(Convolution) 신경망은 전방 신경망에 속합니다. 순환 신경망으로는 RNN과 LSTM이 있습니다.
- 얕은 신경망과 깊은 신경망: 은닉층이 1~2개 정도인 신경망을 얕은 신경망이라고 하며 그 이상의 은닉층을 가지고 있으면 깊은 신경망이라고 합니다. 깊은 신경망을 딥러닝(deep learning)이라고도 합니다.
- 결정적(deterministic) 신경망과 확률적(stochastic) 신경망: 결정적 신경망은 입력이 같으면 출력도 항상 같게나오는 반면 확률적 신경망은 계산 과정에 난수를 사용하여 매번 다른 출력이 나올 수 있습니다. 확률적 신경망으로는 RBN(Radial Basis Network)과 DBN(Deep Belief Network)이 있습니다.
여기서는 비교적 간단하게 분류와 회귀에 사용할 수 있는 다층 퍼셉트론(MLP)에 대해서 다룹니다.
다층 퍼셉트론¶
다층 퍼셉트론은 선형 모델의 일반화된 모형이라고 볼 수 있습니다. 일반적인 선형모델의 예측 공식은 다음과 같습니다.
\(\hat{y}\)은 입력된 특징 \(x_i\)들과 학습하여 얻는 가중치 \(w_i\)들을 합하여 얻어진 값이라고 볼 수 있습니다.
In [358]: lr_graph = mglearn.plots.plot_logistic_regression_graph()
.....: gv_src = graphviz.Source(lr_graph, filename='_static/images/single_percept_gv', format='svg')
.....: gv_src.render()
.....:
Out[360]: '_static/images/single_percept_gv.svg'
다층 퍼셉트론에서는 가중치 합을 만드는 과정이 여러번 반복되며 중간 단계를 구성하는 은닉층을 계산하고 이를 이용하여 최종 결과를 만들기 위해 가중치 계산을 다시 합니다.
In [361]: lr_graph = mglearn.plots.plot_single_hidden_layer_graph()
.....: gv_src = graphviz.Source(lr_graph, filename='_static/images/single_hidden_layer_gv', format='svg')
.....: gv_src.render()
.....:
Out[363]: '_static/images/single_hidden_layer_gv.svg'
여러 은닉층마다 가중치 합을 계산하는 것은 결론적으로는 하나의 가중치합을 계산하는 것과 같습니다. 즉 하나의 선형모델을 만드는 것과 같습니다. 이러한 선형모델을 더 강력하게 만들려면 각 은닉층의 가중치 합을 계산한 후 그 결과에 비선형 함수인 렐루(RELU, rectified linear unit)나 하이퍼탄젠트(hyper tangent)를 적용합니다. 렐루 함수는 0이하를 잘라버리고, tanh 함수는 낮은 입력값에 대해서는 -1, 큰 입력값에 대해서는 +1을 출력합니다. 이런 비선형 함수를 이용해 신경망이 선형 모델보다 더 복잡한 함수를 학습할 수 있습니다.
In [364]: line = np.linspace(-3, 3, 100)
.....: plt.clf()
.....: plt.plot(line, np.tanh(line), label='tanh')
.....: plt.plot(line, np.maximum(line, 0), label='relu')
.....: plt.legend(loc='best')
.....: plt.xlabel('x')
.....: plt.ylabel('relu(x), tanh(x)')
.....:
Out[366]: [<matplotlib.lines.Line2D at 0x156c20ddb38>]
Out[367]: [<matplotlib.lines.Line2D at 0x156c20e7080>]
Out[368]: <matplotlib.legend.Legend at 0x156c1bfd780>
Out[369]: Text(0.5,0,'x')
Out[370]: Text(0,0.5,'relu(x), tanh(x)')
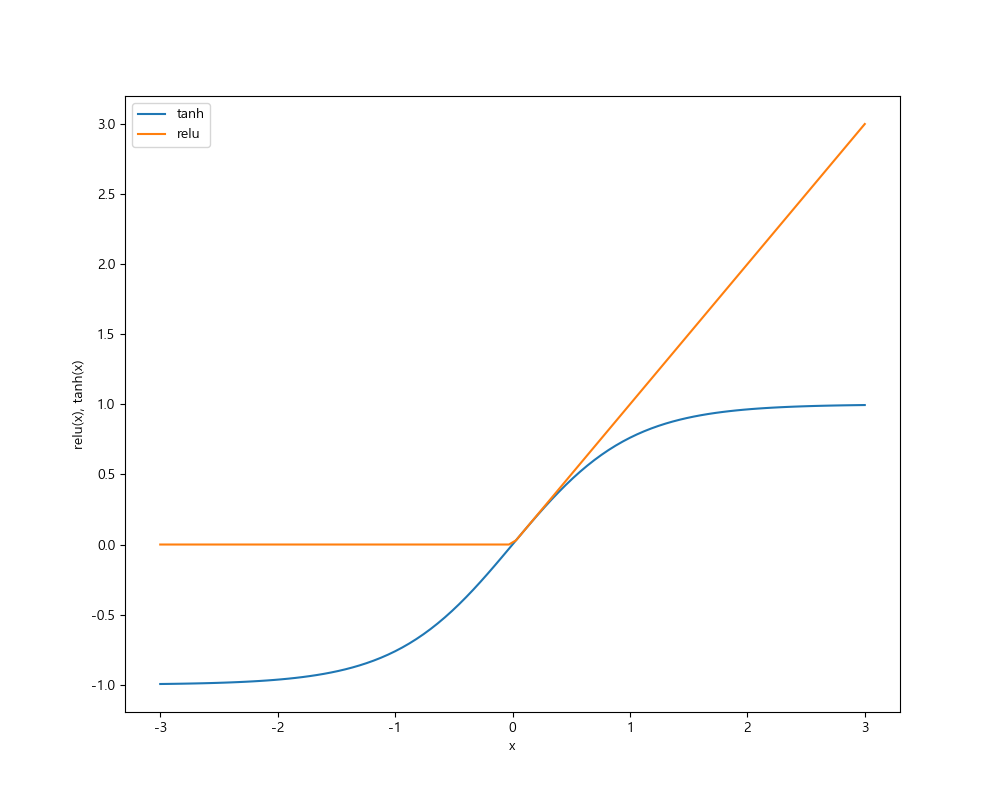
은닉층이 1개이고 3개의 노드를 갖는 위의 그림의 신경망으로 회귀분석을 할 때 \(\hat{y}\)을 계산하기 위한 공식은 다음과 같습니다. 활성함수(active function)으로 tanh를 사용합니다.
\(w\)는 입력 \(x\)와 은닉층 \(h\)와 사이의 가중치이고, \(v\)는 은닉층 \(h\)와 출력 \(\hat{y}\) 사이의 가중치입니다. \(v\)와 \(w\)는 훈련 집합에 의해서 학습된 결과로 결정되고 \(\hat{y}\)은 계산된 출력값, \(h\)는 활성함수에 의해서 출력된 값입니다.
우리가 정해야하는 중요한 매개변수는 은닉층 노드의 갯수입니다. 복잡합 데이터셋에 대해서는 1만개가 넘을 수도 있습니다. 다음과 같이 은닉층을 더 추가할 수 있습니다.
In [371]: two_hidden = mglearn.plots.plot_two_hidden_layer_graph()
.....: gv_src = graphviz.Source(two_hidden, filename='_static/images/two_hidden_layer_gv', format='svg')
.....: gv_src.render()
.....:
Out[373]: '_static/images/two_hidden_layer_gv.svg'
이와 같이 많은 은닉층으로 이루어진 신경망을 딥러닝(deep learning)이라고 부릅니다.
신경망 튜닝¶
two_moons 데이터셋에 분류를 위한 다층퍼셉트론 구현인 MLPClassifier를 적용해봅니다.
In [374]: from sklearn.neural_network import MLPClassifier
.....: from sklearn.datasets import make_moons
.....:
.....: X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
.....:
.....: X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
.....:
.....: mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train)
.....: plt.clf()
.....: mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=0.3)
.....: mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
.....: plt.xlabel("특성 0")
.....: plt.ylabel("특성 1")
.....:
Out[381]:
[<matplotlib.lines.Line2D at 0x156c2148b70>,
<matplotlib.lines.Line2D at 0x156c2148c88>]
Out[382]: Text(0.5,0,'특성 0')
Out[383]: Text(0,0.5,'특성 1')
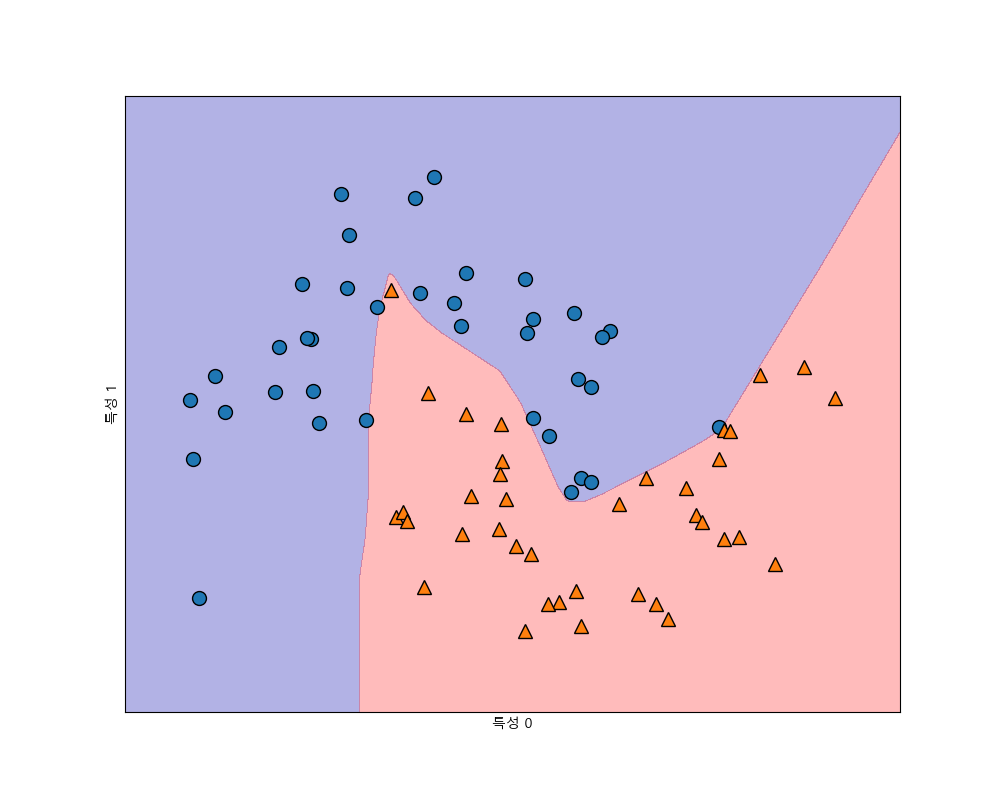
MLPClassifier 기본값으로 은닉층은 1개이고 은닉층의 노드갯수는 100개, 활성함수는 relu입니다. solver=’lbfgs’는 가중치 최적화에 사용되는 알고리즘이고 기본값은 adam입니다.
은닉층의 노드의 갯수를 10개로 줄여보겠습니다.
In [384]: mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=(10,))
.....: mlp.fit(X_train, y_train)
.....: plt.clf()
.....: mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=0.3)
.....: mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
.....: plt.xlabel("특성 0")
.....: plt.ylabel("특성 1")
.....:
Out[385]:
MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,
beta_2=0.999, early_stopping=False, epsilon=1e-08,
hidden_layer_sizes=(10,), learning_rate='constant',
learning_rate_init=0.001, max_iter=200, momentum=0.9,
nesterovs_momentum=True, power_t=0.5, random_state=0, shuffle=True,
solver='lbfgs', tol=0.0001, validation_fraction=0.1, verbose=False,
warm_start=False)
Out[388]:
[<matplotlib.lines.Line2D at 0x156c21896a0>,
<matplotlib.lines.Line2D at 0x156c21897b8>]
Out[389]: Text(0.5,0,'특성 0')
Out[390]: Text(0,0.5,'특성 1')
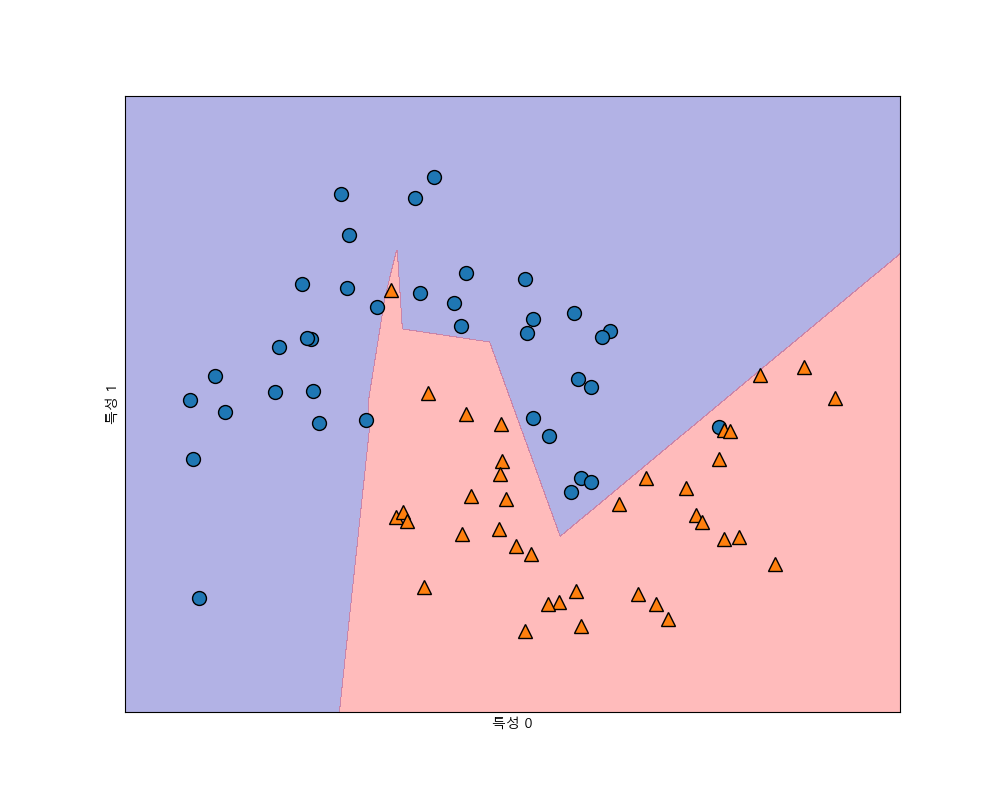
더 부드러운 경계를 위해서는 은닉층을 추가하거나 활성함수로 tanh를 사용할 수 있습니다.
다음은 은닉층이 2개이고 은닉층의 노드의 개수는 10개씩(hidden_layer_sizes=(10, 10)) 입니다.
In [391]: mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=(10, 10))
.....: mlp.fit(X_train, y_train)
.....: plt.clf()
.....: mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=0.3)
.....: mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
.....: plt.xlabel("특성 0")
.....: plt.ylabel("특성 1")
.....:
Out[392]:
MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,
beta_2=0.999, early_stopping=False, epsilon=1e-08,
hidden_layer_sizes=(10, 10), learning_rate='constant',
learning_rate_init=0.001, max_iter=200, momentum=0.9,
nesterovs_momentum=True, power_t=0.5, random_state=0, shuffle=True,
solver='lbfgs', tol=0.0001, validation_fraction=0.1, verbose=False,
warm_start=False)
Out[395]:
[<matplotlib.lines.Line2D at 0x156c21b0f60>,
<matplotlib.lines.Line2D at 0x156c21ba0b8>]
Out[396]: Text(0.5,0,'특성 0')
Out[397]: Text(0,0.5,'특성 1')
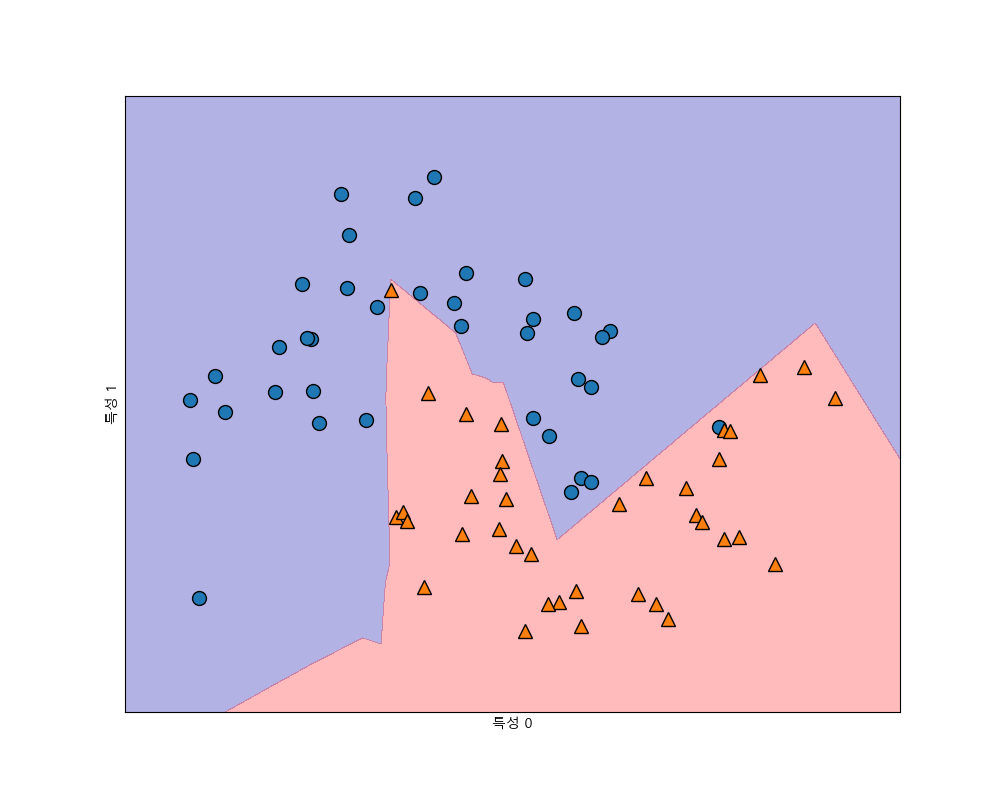
다음은 10개의 노드를 가진 2개의 은닉층과 tanh 활성함수를 사용한 것입니다.
In [398]: mlp = MLPClassifier(solver='lbfgs', activation='tanh', random_state=0, hidden_layer_sizes=(10, 10))
.....: mlp.fit(X_train, y_train)
.....: plt.clf()
.....: mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=0.3)
.....: mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
.....: plt.xlabel("특성 0")
.....: plt.ylabel("특성 1")
.....:
Out[399]:
MLPClassifier(activation='tanh', alpha=0.0001, batch_size='auto', beta_1=0.9,
beta_2=0.999, early_stopping=False, epsilon=1e-08,
hidden_layer_sizes=(10, 10), learning_rate='constant',
learning_rate_init=0.001, max_iter=200, momentum=0.9,
nesterovs_momentum=True, power_t=0.5, random_state=0, shuffle=True,
solver='lbfgs', tol=0.0001, validation_fraction=0.1, verbose=False,
warm_start=False)
Out[402]:
[<matplotlib.lines.Line2D at 0x156c21eba90>,
<matplotlib.lines.Line2D at 0x156c21ebba8>]
Out[403]: Text(0.5,0,'특성 0')
Out[404]: Text(0,0.5,'특성 1')
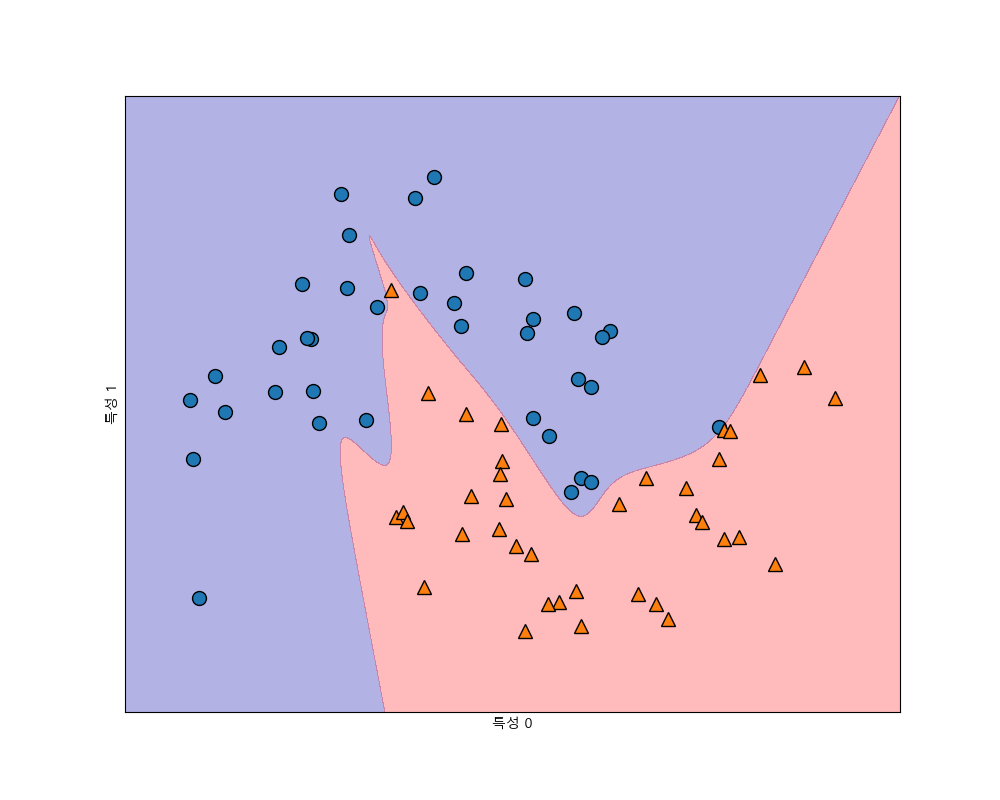
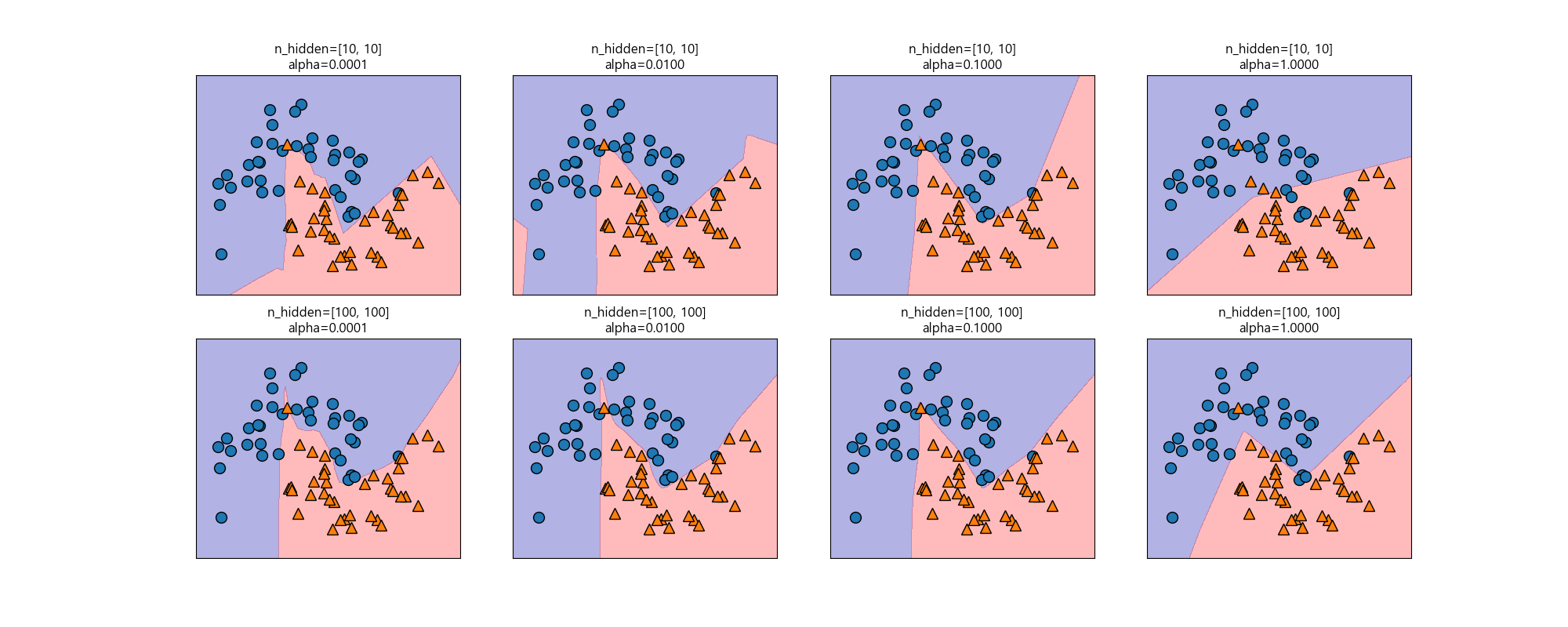
릿지 회귀와 선형 분류기에서처럼 L2 규제를 사용해 가중치를 0에 가깝게해서 모델의 복잡도를 제어할 수 있습니다. MLPClassifier의 alpha를 이용해 복잡도를 제어할 수 있습니다. 기본값은 0.0001로 규제가 거의 없습니다. 다음은 노드의 갯수가 각각 10, 100개인 은닉층 2개를 사용하고 alpha값을 변경하며 모델의 변화를 살펴봅니다.
In [405]: plt.clf()
.....: fig, axes = plt.subplots(2, 4, figsize=(20, 8))
.....: for axx, n_hidden_nodes in zip(axes, [10, 100]):
.....: for ax, alpha in zip(axx, [0.0001, 0.01, 0.1, 1]):
.....: mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[n_hidden_nodes, n_hidden_nodes], alpha=alpha)
.....: mlp.fit(X_train, y_train)
.....: mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=0.3, ax=ax)
.....: mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, ax=ax)
.....: ax.set_title("n_hidden=[{}, {}]\nalpha={:.4f}".format(n_hidden_nodes, n_hidden_nodes, alpha))
.....:
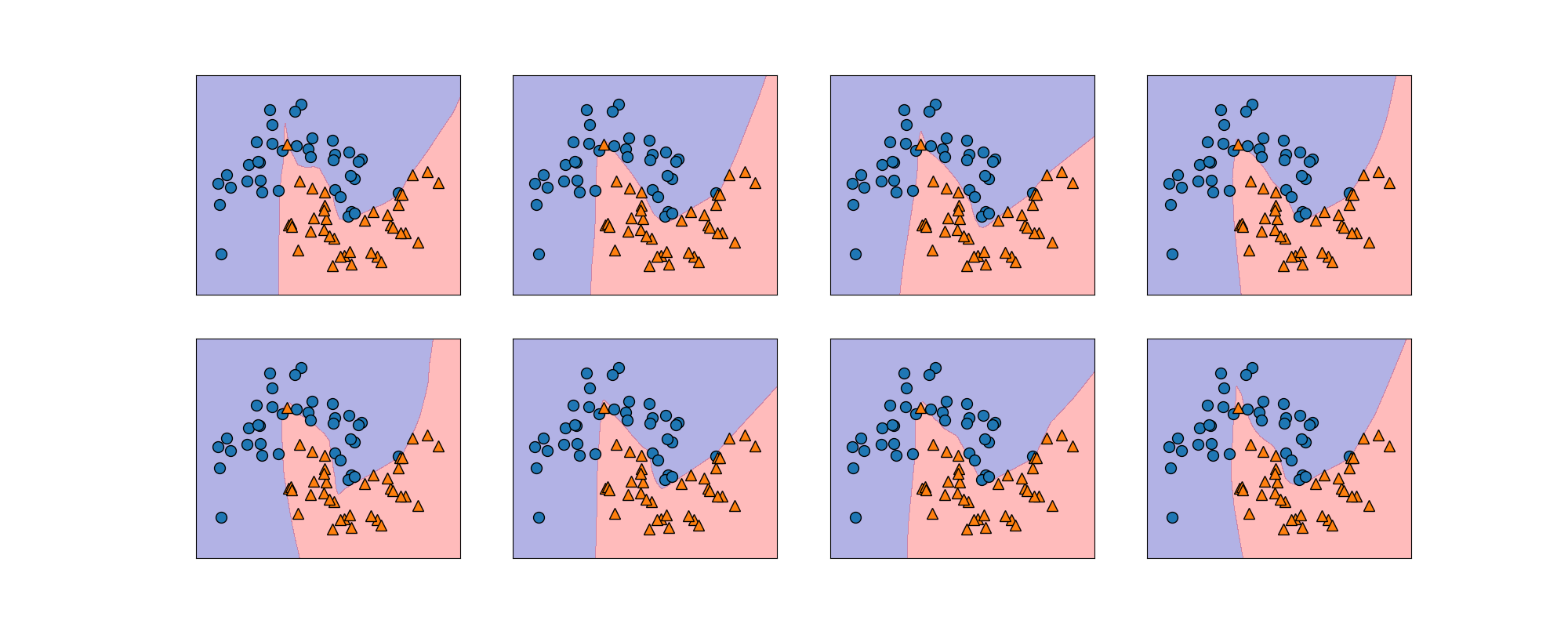
신경망에서는 학습을 시작하기 전에 가중치를 무작위로 설정하며 이 값이 모델의 학습에 영향을 미치게 됩니다. 신경망이 크고 복잡도가 적절하면 이런 것이 정확도에 미치는 영향이 작지만 항상 기억하고 있어야합니다. 다음은 초기화를 다르게해서 만들 모델입니다.
In [408]: plt.clf()
.....: fig, axes = plt.subplots(2, 4, figsize=(20, 8))
.....: for i, ax in enumerate(axes.ravel()):
.....: mlp = MLPClassifier(solver='lbfgs', random_state=i, hidden_layer_sizes=(100, 100))
.....: mlp.fit(X_train, y_train)
.....: mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=0.3, ax=ax)
.....: mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, ax=ax)
.....:
실제 데이터인 유방암 데이터셋에 MLPClassifier를 적용해보겠습니다.
In [411]: print("유방암 데이터의 특징별 최대값:\n{}".format(cancer.data.max(axis=0)))
유방암 데이터의 특징별 최대값:
[2.811e+01 3.928e+01 1.885e+02 2.501e+03 1.634e-01 3.454e-01 4.268e-01
2.012e-01 3.040e-01 9.744e-02 2.873e+00 4.885e+00 2.198e+01 5.422e+02
3.113e-02 1.354e-01 3.960e-01 5.279e-02 7.895e-02 2.984e-02 3.604e+01
4.954e+01 2.512e+02 4.254e+03 2.226e-01 1.058e+00 1.252e+00 2.910e-01
6.638e-01 2.075e-01]
In [412]: X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)
.....:
.....: mlp = MLPClassifier(random_state=42)
.....: mlp.fit(X_train, y_train)
.....:
.....: print("훈련 집합 정확도: {:.2f}".format(mlp.score(X_train, y_train)))
.....: print("테스트 집합 정확도: {:.2f}".format(mlp.score(X_test, y_test)))
.....:
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������Out[414]:
MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,
beta_2=0.999, early_stopping=False, epsilon=1e-08,
hidden_layer_sizes=(100,), learning_rate='constant',
learning_rate_init=0.001, max_iter=200, momentum=0.9,
nesterovs_momentum=True, power_t=0.5, random_state=42, shuffle=True,
solver='adam', tol=0.0001, validation_fraction=0.1, verbose=False,
warm_start=False)
훈련 집합 정확도: 0.91
테스트 집합 정확도: 0.88
MLP의 정확도가 다른 모델에 비해서 높은 편이 아닌 걸 확인할 수 있습니다. SVC 예제에서 보았듯이 데이터의 스케일이 영향을 미칠수 있었듯이 신경망의 입력 특징들을 평균 0, 분산 1이 되도록 변형해봅니다.
In [417]: # 훈련 집합 각 특징의 평균을 계산합니다.
.....: mean_on_train = X_train.mean(axis=0)
.....: # 훈련 집합 각 특징의 표준편차를 계산합니다.
.....: std_on_train = X_train.std(axis=0)
.....: # 평균 0, 표준편차 1인 데이터로 변환합니다.
.....: X_train_scaled = (X_train - mean_on_train) / std_on_train
.....: # 테스트 집합도 같이 변환합니다.
.....: X_test_scaled = (X_test - mean_on_train) / std_on_train
.....:
.....: mlp = MLPClassifier(random_state=0)
.....: mlp.fit(X_train_scaled, y_train)
.....:
.....: print("훈련 집합 정확도: {:.3f}".format(mlp.score(X_train_scaled, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(mlp.score(X_test_scaled, y_test)))
.....:
Out[426]:
MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,
beta_2=0.999, early_stopping=False, epsilon=1e-08,
hidden_layer_sizes=(100,), learning_rate='constant',
learning_rate_init=0.001, max_iter=200, momentum=0.9,
nesterovs_momentum=True, power_t=0.5, random_state=0, shuffle=True,
solver='adam', tol=0.0001, validation_fraction=0.1, verbose=False,
warm_start=False)
훈련 집합 정확도: 0.991
테스트 집합 정확도: 0.965
스케일 결과 정확도가 좋아진 것을 확인할 수 있습니다. 경고는 adam 알고리즘 사용할 때 나오는 것으로 반복 횟수를 늘리면 됩니다.
In [429]: mlp = MLPClassifier(max_iter=1000, random_state=0)
.....: mlp.fit(X_train_scaled, y_train)
.....:
.....: print("훈련 집합 정확도: {:.3f}".format(mlp.score(X_train_scaled, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(mlp.score(X_test_scaled, y_test)))
.....:
Out[430]:
MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,
beta_2=0.999, early_stopping=False, epsilon=1e-08,
hidden_layer_sizes=(100,), learning_rate='constant',
learning_rate_init=0.001, max_iter=1000, momentum=0.9,
nesterovs_momentum=True, power_t=0.5, random_state=0, shuffle=True,
solver='adam', tol=0.0001, validation_fraction=0.1, verbose=False,
warm_start=False)
훈련 집합 정확도: 0.993
테스트 집합 정확도: 0.972
일반화 성능을 올리기 위해 복잡도를 낮춰보겠습니다. alpha 변수를 1로 증가시켜 보겠습니다.
In [433]: mlp = MLPClassifier(max_iter=1000, alpha=1, random_state=0)
.....: mlp.fit(X_train_scaled, y_train)
.....:
.....: print("훈련 집합 정확도: {:.3f}".format(mlp.score(X_train_scaled, y_train)))
.....: print("테스트 집합 정확도: {:.3f}".format(mlp.score(X_test_scaled, y_test)))
.....:
Out[434]:
MLPClassifier(activation='relu', alpha=1, batch_size='auto', beta_1=0.9,
beta_2=0.999, early_stopping=False, epsilon=1e-08,
hidden_layer_sizes=(100,), learning_rate='constant',
learning_rate_init=0.001, max_iter=1000, momentum=0.9,
nesterovs_momentum=True, power_t=0.5, random_state=0, shuffle=True,
solver='adam', tol=0.0001, validation_fraction=0.1, verbose=False,
warm_start=False)
훈련 집합 정확도: 0.988
테스트 집합 정확도: 0.972
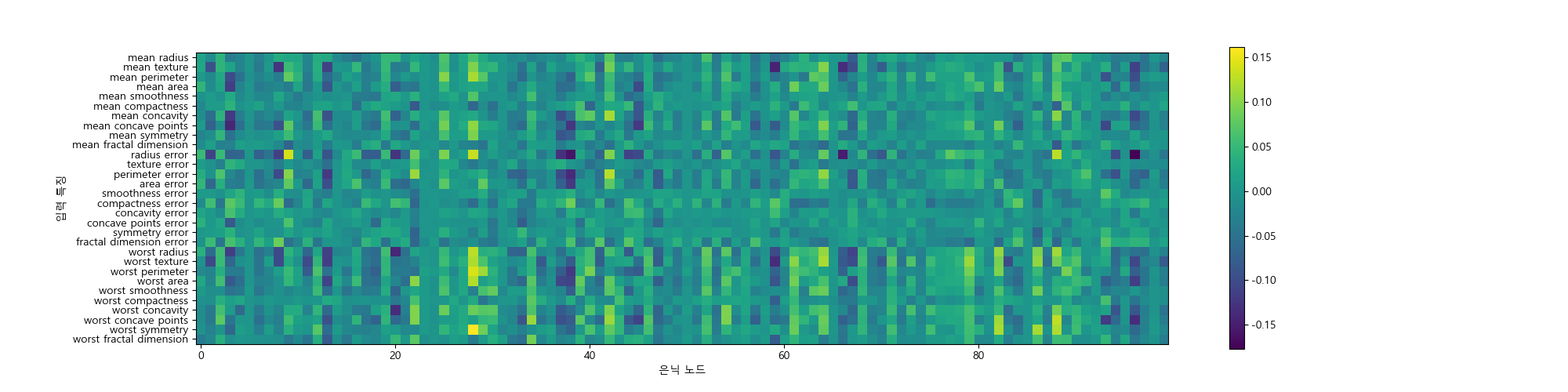
다음은 유방암 데이터셋의 입력과 은닉층 사이의 학습된 가중치를 보여줍니다. 30개의 특징과 100개의 노드에 해당하는 그림입니다.
In [437]: plt.clf()
.....: plt.figure(figsize=(20, 5))
.....: plt.imshow(mlp.coefs_[0], interpolation='none', cmap='viridis');
.....: plt.yticks(range(30), cancer.feature_names);
.....: plt.xlabel("은닉 노드");
.....: plt.ylabel("입력 특징");
.....: plt.colorbar();
.....:
장단점¶
신경망의 주요 장점은 대량의 데이터에 내재된 정보를 찾아내고 매우 복잡한 모델을 만들수 있다는 점입니다. 충분한 연산 시간과 데이터를 주고 매개변수를 세심하게 조정하면 신경망은 다른 기계학습 알고리즘들을 뛰어넘는 성과를 거둘 수 있습니다.
단점으로는 신경망은 학습이 오래 걸립니다. 또한 데이터 전처리에 주의해야 합니다. SVM과 비슷하게 모든 특징이 같은 의미를 가진 동질의 데이터에 잘 작동합니다. 다른 종류의 특징을 가진 데이터라면 트리 기반 모델이 더 작동할 수 있습니다. 신경망 매개변수 튜닝은 예술에 가까운 일입니다.
참고 사이트
| [1] | https://datascienceschool.net/view-notebook/3e7aadbf88ed4f0d87a76f9ddc925d69/ |