기계학습(Machine Learning)¶
기계학습이란 특정한 응용 영역에서 발생하는 데이터(경험)를 이용하여 높은 성능으로 문제를 해결하는 컴퓨터 프로그램을 만드는 작업을 뜻한다. [1]
기계학습 이전에는 주어진 문제를 해결하기 위해 그 문제에 적합한 지식들을 프로그램에 심어놓는 방식으로 접근했다. 예를 들면 숫자 8을 인식하기 위해서 구멍이 2개 있는 형태를 인식하도록 프로그램에 심어놓는 것이다. 하지만 이러한 방식으로는 사람이 인식하는 숫자 형태를 구분할 수 없다는 것을 깨닫는다. 따라서 일일이 모든 경우를 컴퓨터에 설명하려고 하는 것을 포기하고 다양한 데이터를 수집하여 알 고리즘에 입력하여 학습을 하게 만들어 더 적합한 값이 되도록 향상시키도록 하는 것이 기계학습이다.
개요¶
용어¶
- 표본(sample)
- 자료의 하나 개체, 행 또는 데이터 포인트라고 부릅니다. 기호로는 벡터 \(x = (x_1, x_2, ..., x_n)\)으로 나타냅니다. 표본을 이용해서 예측을 합니다.
- 특징(feature)
- 자료의 열
- 레이블(label)
- 목표(target)라고도 불립니다. 기호로는 y로 나타냅니다.
- 훈련 집합(training set)
- 또는 학습 집합(learning set)
- 테스트 집합(testing set)
- 학습된 모델이 어느 정도 정확한지를 평가하는 집합입니다.
기계학습 분류¶
- 지도학습(Supervised Learning)
지도학습은 데이터의 측정된 특징(feature)과 데이터와 관련된 레이블(label) 사이의 관계를 모델링하는 것입니다. [2]
- 분류(classification): 둘 이상의 이산적인 범부로 레이블을 예측하는 모델
- 회귀(regression): 연속적인 레이블을 예측하는 모델
- 비지도학습(Unsupervised Learning)
비지도학습은 레이블을 참조하지 않고 데이터세트의 특징을 모델링하는 것입니다.
- 군집화(clustering): 데이터의 개별 그룹을 탐지하고 식별하는 모델
- 차원축소(dimensionality reduction): 고차원 데이터의 저차원 구조를 탐지하고 식별하는 모델
- 밀도 추정(density estimation)
그 밖에 준지도 학습(semi-supervised learning), 강화학습(reinforcement learning) 등이 있습니다.
기계학습 절차¶
주어진 자료를 이용해 해결하기 원하는 문제에 적합한 모델을 선택해서 기계학습을 통해 학습을 자료에 최적화된 답을 찾아냅니다. 찾아낸 모델에 검증을 위해 테스트 집합을 적용해 적당한 모델인지를 검증합니다.
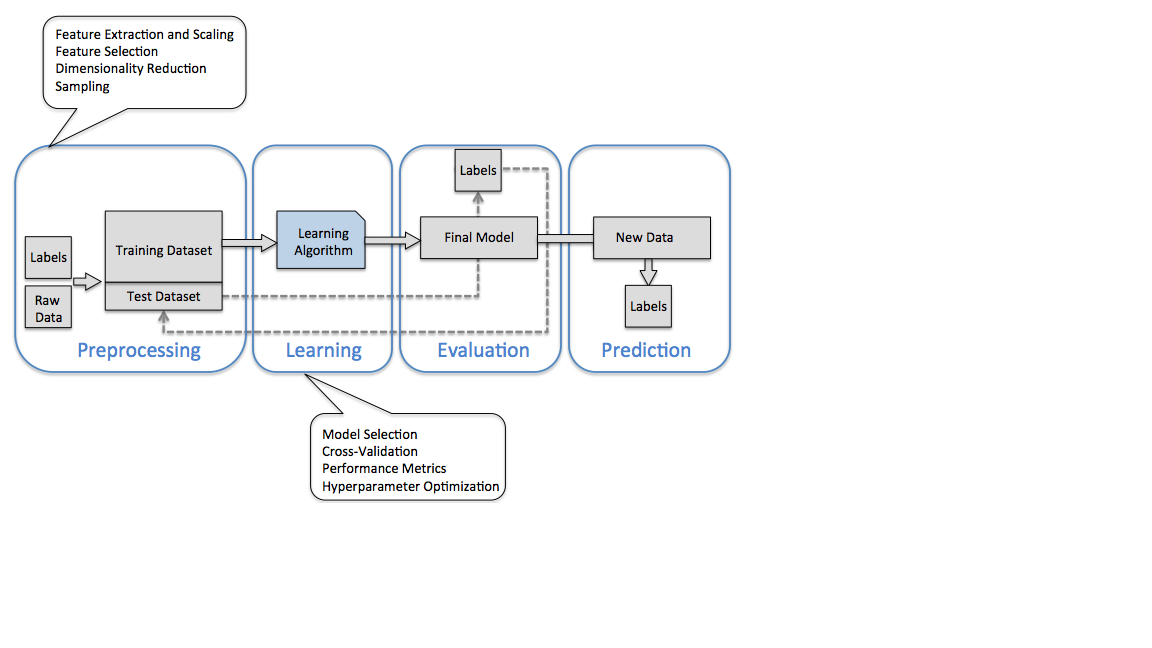
문제와 자료 이해¶
획득한 자료로 무엇을 하는 것인지를 생각해봐야 합니다. 기계학습 모델을 만들기 전에 반드시 다음 질문을 해보고 만드는 과정 중에 마음에 새겨두어야 할 것입니다.
- 어떤 질문에 대한 답을 원하는가?
- 가지고 있는 데이터가 원하는 답을 줄 수 있는가?
- 내 질문을 기계학습의 문제로 가장 잘 기술하는 방법은 무엇인가?
- 문제를 풀기에 충분한 데이터를 모았는가?
- 내가 추출한 데이터의 특징은 무엇이며 좋은 예측을 만들어 낼 수 있을 것인가?
- 기계학습 응용의 성과를 어떻게 측정할 수 있는가?
- 기계학습 완성품이 다른 연구나 제품과 어떻게 협력할 수 있는가?
scikit-learn¶
머신러닝을 위한 라이브러리들로는 scikit-learn, Keras, TensorFlow, Theano 등이 있습니다.
scikit-learn 추정기(estimator) API¶
scikit-learn API는 기본적으로 다음과 같은 절차를 이용합니다.
- scikit-learn으로부터 적절한 추정기 클래스를 불러옵니다.
- 선택된 클래스 인스턴스에 모델의 초모수(hyperparameter)를 선택합니다.
- 데이터를 특징 행렬과 목표 벡터로 분리합니다.
- 모델 인스턴스의 fit() 메소드를 이용해 데이터에 적합시킵니다.
- 모델을 새로운 데이터에 적용합니다.
- 지도학습인 경우는 predict() 메소드를 이용해 레이블을 예측합니다.
- 비지도학습인 경우는 transform() 이나 predict() 메소드를 이용합니다.
사용 예제¶
scikit-learn API 사용하는 간단한 선형 회귀 예제를 살펴봅니다. 예제를 위해 다음과 같이 간단한 데이터 x, y를 사용합니다.
In [1]: import matplotlib.pyplot as plt
...: import numpy as np
...:
...: rng = np.random.RandomState(42)
...: x = 10 * rng.rand(50)
...: y = 2 * x - 1 + rng.randn(50)
...:
...: fig, ax = plt.subplots()
...: ax.scatter(x, y);
...:
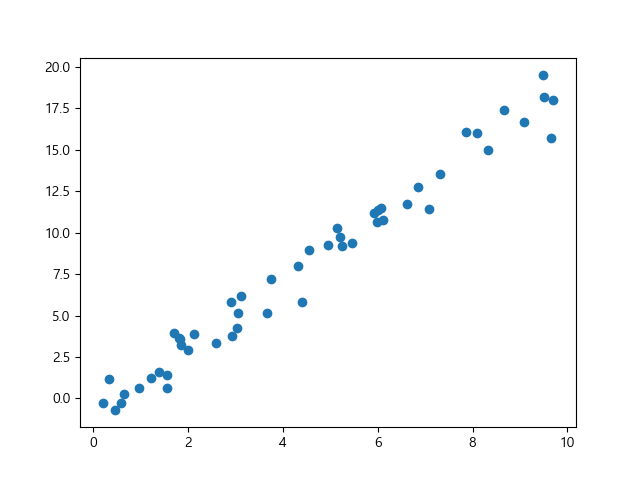
- 모델 클래스를 선택합니다.
scikit-learn에서 모든 모델 클래스는 파이썬 클래스로 표현됩니다. 간단한 회귀 모델을 원하면 LinearRegression 클래스를 불러오면 됩니다.
In [8]: from sklearn.linear_model import LinearRegression
...:
- 선택된 클래스 LinearRegression을 인스턴스화하고 모델 초모수
fit_intercept=True를 설정해 절편을 적합합니다.
In [9]: model = LinearRegression(fit_intercept=True)
- 데이터를 특징 행렬과 목표 벡터로 분리합니다.
In [10]: X = x[:, np.newaxis]
....: X.shape
....:
Out[11]: (50, 1)
- 모델을 데이터에 적합시킵니다. 즉 학습을 시킵니다.
In [12]: model.fit(X, y)
Out[12]: LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
학습된 모델 모수는 이름 뒤에 밑줄 표시가 붙습니다.
In [13]: model.coef_
Out[13]: array([1.9776566])
In [14]: model.intercept_
Out[14]: -0.9033107255311164
- 새로운 데이터에 대한 레이블을 예측합니다.
In [15]: xfit = np.linspace(-1, 11)
In [16]: Xfit = xfit[:, np.newaxis]
....: yfit = model.predict(Xfit)
....:
결과를 시각화해 봅니다.
In [18]: ax.cla()
....: ax.scatter(x, y)
....: ax.plot(xfit, yfit)
....:
Out[19]: <matplotlib.collections.PathCollection at 0x156973e4400>
Out[20]: [<matplotlib.lines.Line2D at 0x15697293390>]
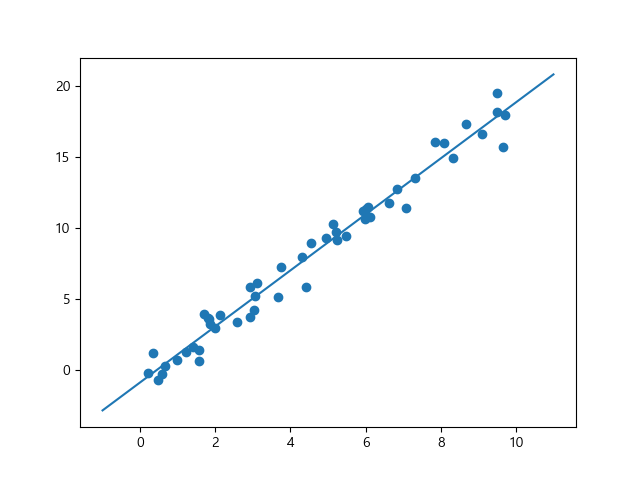
scikit-learn 활용¶
붓꽃 데이터를 이용해서 새로 채집한 붓꽃의 품종을 예측하는 기계학습 모델을 만드는 것이 목표입니다. 붓꽃 데이터는 품종에 대한 자료를 포함하고 있으므로 지도학습에 속합니다. 어떤 품종에 속할 것인지를 알아내는 것은 분류(classification)에 속하는 문제입니다.
데이터 표현 방식¶
scikit-learn에서 사용하는 데이터 형식에 대해서 살펴봅니다. 1936년 로널드 피셔가 분석했던 붓꽃 데이터를 사용합니다. load_iris 함수를 이용해서 불러올 수 있습니다.
In [21]: from sklearn.datasets import load_iris
....: iris = load_iris()
....:
load_iris가 반환한 객체는 파이썬 사전형과 비슷한 Bunch 클래스입니다. 키와 값으로 구성됩니다.
In [23]: iris.keys()
Out[23]: dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names'])
DESCR 키에는 데이터에 대한 간단한 설명이 포함되어 있습니다.
In [24]: print(iris.DESCR)
Iris Plants Database
====================
Notes
-----
Data Set Characteristics:
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
- Iris-Setosa
- Iris-Versicolour
- Iris-Virginica
:Summary Statistics:
============== ==== ==== ======= ===== ====================
Min Max Mean SD Class Correlation
============== ==== ==== ======= ===== ====================
sepal length: 4.3 7.9 5.84 0.83 0.7826
sepal width: 2.0 4.4 3.05 0.43 -0.4194
petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)
petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)
============== ==== ==== ======= ===== ====================
:Missing Attribute Values: None
:Class Distribution: 33.3% for each of 3 classes.
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
This is a copy of UCI ML iris datasets.
http://archive.ics.uci.edu/ml/datasets/Iris
The famous Iris database, first used by Sir R.A Fisher
This is perhaps the best known database to be found in the
pattern recognition literature. Fisher's paper is a classic in the field and
is referenced frequently to this day. (See Duda & Hart, for example.) The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant. One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.
References
----------
- Fisher,R.A. "The use of multiple measurements in taxonomic problems"
Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
Mathematical Statistics" (John Wiley, NY, 1950).
- Duda,R.O., & Hart,P.E. (1973) Pattern Classification and Scene Analysis.
(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
Structure and Classification Rule for Recognition in Partially Exposed
Environments". IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-2, No. 1, 67-71.
- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions
on Information Theory, May 1972, 431-433.
- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II
conceptual clustering system finds 3 classes in the data.
- Many, many more ...
target_names의 값은 붓꽃 품종의 이름이 문자열 배열로 들어 있습니다.
In [25]: iris.target_names
Out[25]: array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
feature_names의 값은 각 열을 나타내는 특징을 설명하는 문자열 리스트입니다.
In [26]: iris.feature_names
Out[26]:
['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
실제 데이터는 data와 target의 값에 들어 있습니다. data는 꽃잎의 길이, 폭, 꽃받침의 길와 폭에 대한 값을 가지고 있습니다.
In [27]: iris.data[:5]
Out[27]:
array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],
[5. , 3.6, 1.4, 0.2]])
즉 특징의 갯수가 4개이고 표본의 갯수는 150개로 구성되어 있습니다.
In [28]: iris.data.shape
Out[28]: (150, 4)
target에는 붓꽃 품종에 대응되는 숫자가 들어 있습니다. target_names에 표시된 것과 같이 0은 setosa, 1은 versicolor, 2는 virginica입니다.
In [29]: iris.target[:5]
Out[29]: array([0, 0, 0, 0, 0])
훈련집합과 테스트 집합¶
모델을 학습시키기 위해서는 훈련 데이터가 필요하고 이렇게 학습된 모델 성능을 측정하기 위해서는 테스트 데이터가 필요합니다. 이러한 테스트 데이터를 테스트 집합 또는 홀드아웃 집합(hold-out set)이라고도 부릅니다. 또한 훈련 데이터를 훈련 집합이라고도 부릅니다.
scikit-learn은 데이터 집합을 훈련 집합과 테스트 집합으로 분배하는 train_test_split 함수를 제공합니다. 이 함수는 전체 행 중 75%를 훈련 집합으로 뽑고 나머지 25%는 테스트 집합으로 나눕니다.
scikit-learn에서 데이터는 2차원 배열을 나타내는 대문자 X로 표시하고 레이블은 1차원 벡터를 의미하는 y로 표시합니다.
In [30]: from sklearn.model_selection import train_test_split
....: X_train, X_test, y_train, y_test = train_test_split(iris['data'], iris['target'], random_state=0)
....:
train_test_split 함수로 데이터를 나누기 전에 유사 난수 생성기를 사용해 데이터 집합을 무작위로 섞어야 합니다. 그렇지 않으면 데이터가 레이블 순서대로 정렬되어 있기 때문에 뒤쪽 25% 레이블은 모두 2가 됩니다.
In [32]: print(X_train.shape, y_train.shape)
....: print(X_test.shape, y_test.shape)
....:
(112, 4) (112,)
(38, 4) (38,)
자료 분포¶
기계학습 모델을 학습하기 전에 자료의 형태를 살펴보는 것이 먼저 할 일입니다. 시각화를 이용하여 조사하는 것이 좋은 방법입니다.
In [34]: import pandas as pd
....: iris_df = pd.DataFrame(X_train, columns=iris.feature_names)
....: fig.clear()
....: pd.plotting.scatter_matrix(iris_df, c=y_train, figsize=(15, 15), marker='o', hist_kwds={'bins': 20}, s=30, alpha=.8, ax=ax);
....:
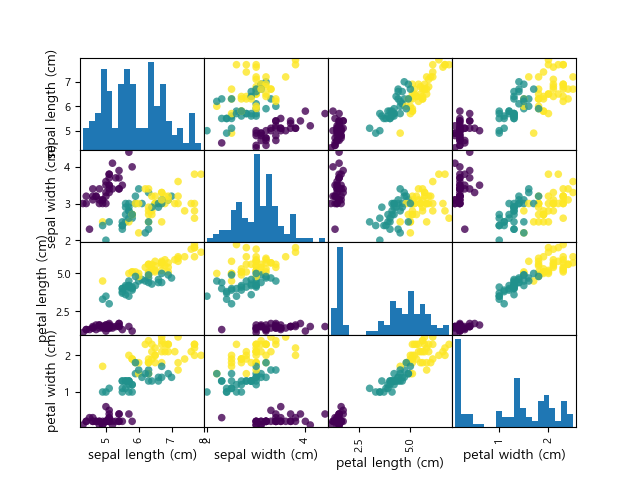
모델 선택 및 학습¶
여기서는 이해하기 쉬운 분류 알고리즘인 k-최근접 이웃 분류기를 사용합니다. 이 모델은 훈련 집합 전체와 예측이 필요한 새로운 데이터와 k 개의 최근접한 이웃들을 찾아 이웃들의 빈도가 가장 높은 이웃의 클래스를 선택하는 방법입니다.
k-최근접 이웃 분류 알고리즘은 KNeighborsClassifier 클래스에 구현되어 있습니다. KNeighborsClassifier에서 가장 중요한 초모수는 이웃의 갯수 k입니다. 여기서는 k=1을 지정하겠습니다.
In [38]: from sklearn.neighbors import KNeighborsClassifier
....: knn = KNeighborsClassifier(n_neighbors=1)
....:
훈련 집합을 이용하여 모델을 학습시킵니다.
In [40]: knn.fit(X_train, y_train)
Out[40]:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=1, p=2,
weights='uniform')
예측¶
새 데이터에 대한 예측을 해봅니다. 꽃받침의 길이가 5cm, 폭이 2.9cm이고 꽃잎의 길이가 1cm, 폭이 0.2cm인 붓꽃이 관찰됐을 때 품종을 예측해 보겠습니다.
In [41]: X_new = np.array([[5, 2.9, 1, 0.2]])
....: X_new.shape
....:
Out[42]: (1, 4)
predict 메소드를 이용해 예측합니다.
In [43]: prdct = knn.predict(X_new)
....: print("예측값: {}, ".format(prdct), "예측한 품종: {}".format(iris['target_names'][prdct]))
....:
예측값: [0], 예측한 품종: ['setosa']
모델 평가하기¶
테스트 집합을 이용해서 학습된 모델이 얼마나 정확한지를 계산합니다.
In [45]: y_pred = knn.predict(X_test)
....: y_pred
....:
Out[46]:
array([2, 1, 0, 2, 0, 2, 0, 1, 1, 1, 2, 1, 1, 1, 1, 0, 1, 1, 0, 0, 2, 1,
0, 0, 2, 0, 0, 1, 1, 0, 2, 1, 0, 2, 2, 1, 0, 2])
In [47]: np.mean(y_pred == y_test)
Out[47]: 0.9736842105263158
일반화, 과대적합, 과소적합¶
한글과 축에 음수 기호 표시를 위해 다음과 같이 설정합니다.
In [48]: from matplotlib import font_manager, rc
....: import matplotlib as mlp
....: font_name = font_manager.FontProperties(fname="c:/Windows/Fonts/malgun.ttf").get_name()
....: rc('font', family=font_name)
....: mlp.rcParams['axes.unicode_minus'] = False # 축에 음수 표시
....:
잡음이 들어간 사인 데이터를 만드는 함수입니다.
In [53]: import numpy as np
....: def make_data(N=30, err=0.1, rseed=1):
....: # 잡음이 들어간 사인함수 값
....: rng = np.random.RandomState(rseed)
....: X = rng.rand(N, 1) ** 2
....: y = np.sin(8 * X).ravel() + err * rng.randn(N)
....: return X, y
....:
In [55]: from sklearn.preprocessing import PolynomialFeatures
....: from sklearn.linear_model import LinearRegression
....: from sklearn.pipeline import make_pipeline
....:
....: def PolynomialRegression(degree=2, **kwargs):
....: return make_pipeline(PolynomialFeatures(degree), LinearRegression(**kwargs))
....:
다음 그래프는 잡음이 들어간 사인 데이터를 다항함수들로 적합한 것입니다.
In [59]: X, y = make_data()
....: xfit = np.linspace(-0.1, 1.0, 500)[:, np.newaxis]
....: degs = [1, 2, 3, 4, 20]
....: fig, ax = plt.subplots(1, len(degs), figsize=(19, 4))
....: for i, deg in enumerate(degs):
....: model = PolynomialRegression(deg).fit(X, y)
....: ax[i].scatter(X.ravel(), y, s=40)
....: ax[i].plot(xfit.ravel(), model.predict(xfit), color='gray')
....: ax[i].axis([-0.1, 1.0, -1.2, 1.2])
....: ax[i].set_title(str(deg) + '차', size=14)
....: fig.tight_layout()
....:
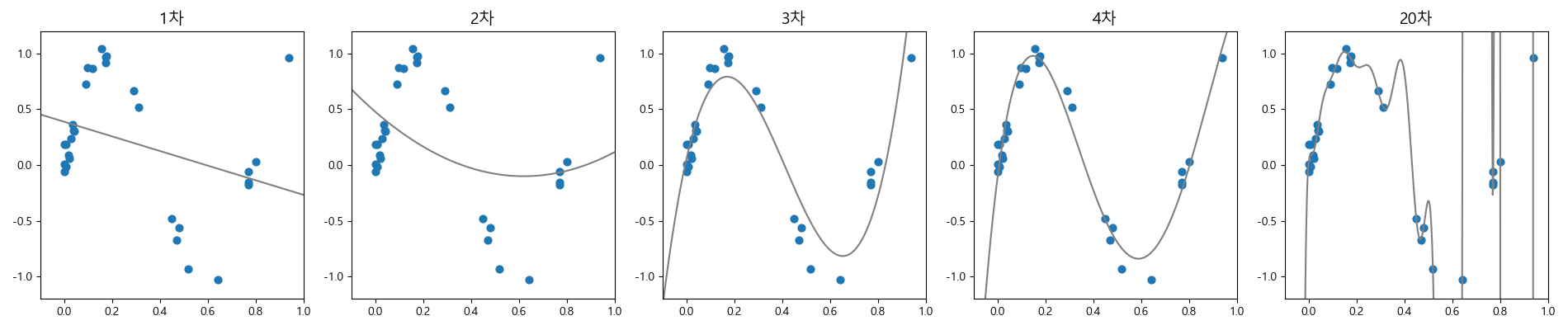
왼쪽에 있는 1, 2차 다항함수로 적합한 그래프는 실제 데이터와 적합한 함수와의 오차가 크게 나는 것을 알 수 있습니다. 이러한 현상을 과소적합(underfitting)이라고 합니다. 이것은 작은 갯수의 모델 매개변수로 복잡한 데이터를 표현할 수 없어서 발생하는 것입니다.
반면에 맨 오른쪽에 있는 20차 다항식은 주어진 데이터를 대부분 지나가며 거의 완벽하게 학습을 한 것을 보여주고 있습니다. 하지만 새로운 데이터를 예측하려고 한다면 데이터가 나타내고 있는 일반적인 모습에 맞는 값을 반환하기 어려울 것입니다. 이러한 현상을 과대적합(overfitting)이라고 합니다. 이러한 현상은 주어진 데이터가 표현하고자 하는 모습보다 너무 많은 매개변수(21개의 계수)를 갖는 다항식으로 표현되었기 때문입니다.
모델이 새로운 데이터에 대해 정확하게 예측할 수 있으면 이를 훈련 집합에서 테스트 집합으로 일반화(generalization)되었다고 합니다.
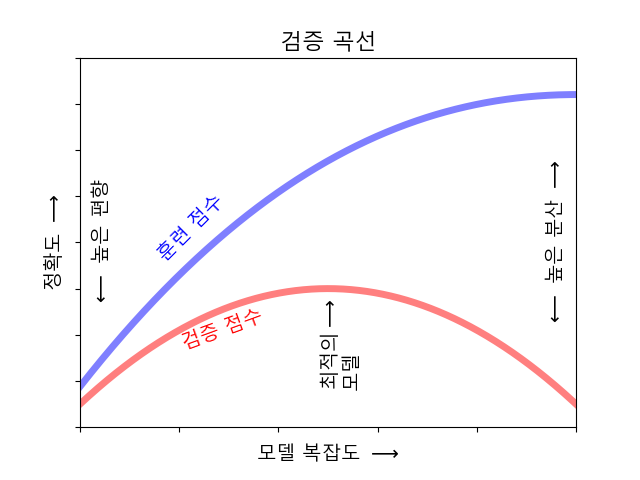
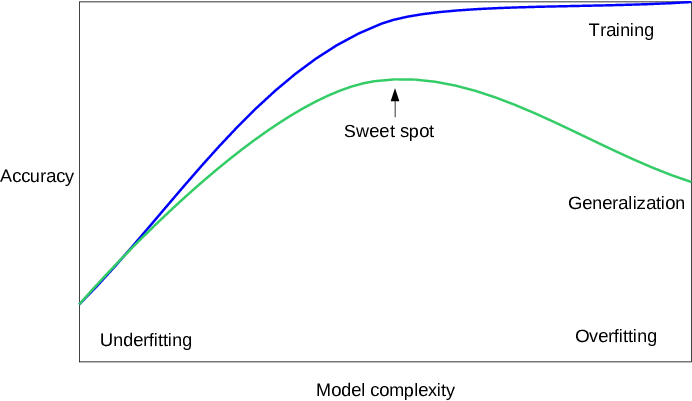
모델을 복잡하게 할 수록 훈련 집합에 대해서는 더 정확히 예측할 수 있습니다. 하지만 너무 복잡해지면 훈련 집합에 너무 민감해져 새로운 데이터에 잘 일반화되지 못합니다. 우리가 찾으려는 모델은 일반화 성능이 최대가 되는 최적화된 모델입니다.
참고 문헌
| [1] | 기계학습(Machine Learning), 오일석, 한빛아카데미, 2017 |
| [2] | 파이썬 데이터 사이언스 핸드북, Jake VanderPlas, 위키북스, 2017 |
| [3] | 파이썬 라이브러리를 활용한 머신러닝(Introduction to Machine Learning with Python), Andreas Muller & Sarah Guido, 한빛미디어, 2017 |