퍼셉트론

사람의 뇌 신경세포 ^neuron의 동작과정을 흉내내어 만든 수학적 모델이 퍼셉트론입니다.

신경세포와 인공 뉴런

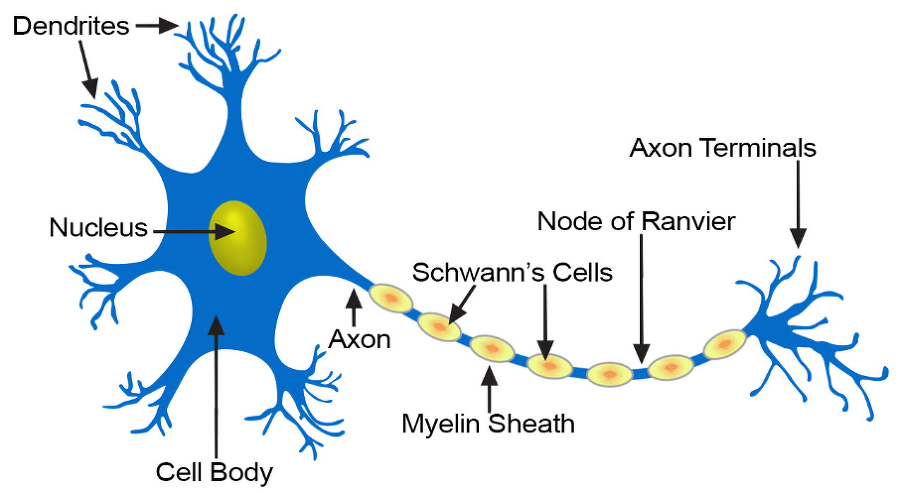
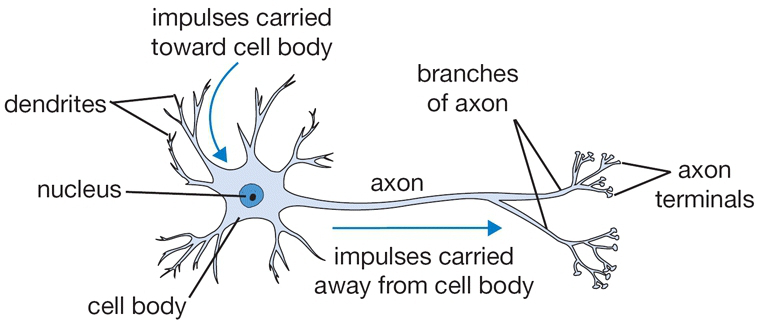
인간의 뇌에는 수십억 개 이상의 뉴런이 있습니다. 뉴런은 화학 및 전기적 신호를 처리하고 전달하는 데 관여하는 인간의 뇌에서 서로 연결된 신경 세포입니다. 가지돌기 ^dendrite는 다른 뉴런으로부터 정보를 받아 세포체 ^{cell body}를 거쳐 축삭 ^axon을 통해서 다른 뉴런으로 신호를 보냅니다.

생물학적 뉴런 대 인공 뉴런

_images/diagram-for-general-view-of-artificial-neuron_2.jpg — 인공뉴런

생물학적 뉴런은 다음 표에서와 같이 인공 뉴런과 비슷합니다.

생물학적 뉴런 대 인공 뉴런 1
생물학적 뉴런	인공 뉴런
세포체(cell body)	노드(node)
가지돌기(dedrite)	입력(input)
시냅스(synapse)	가중치(weight)
축삭(axon)	출력(output)

출처: https://cs231n.github.io/neural-networks-1/

퍼셉트론 개념

퍼셉트론은 로젠 블렛이 1957년에 고안한 알고리즘입니다. 퍼셉트론은 입력 데이터를 2개의 부류중 하나로 분류하는 분류기(classifier)입니다.

퍼셉트론은 학습이 가능한 초창기 신경망 모델로 현대적 의미로 보면 상당히 원시적인 신경망으로 볼 수 있습니다. 하지만 노드, 가중치, 층과 같은 개념이 도입되어 딥러닝을 포함하여 현대 신경망의 중요한 구성요소들을 이해하는데 의미가 있습니다.

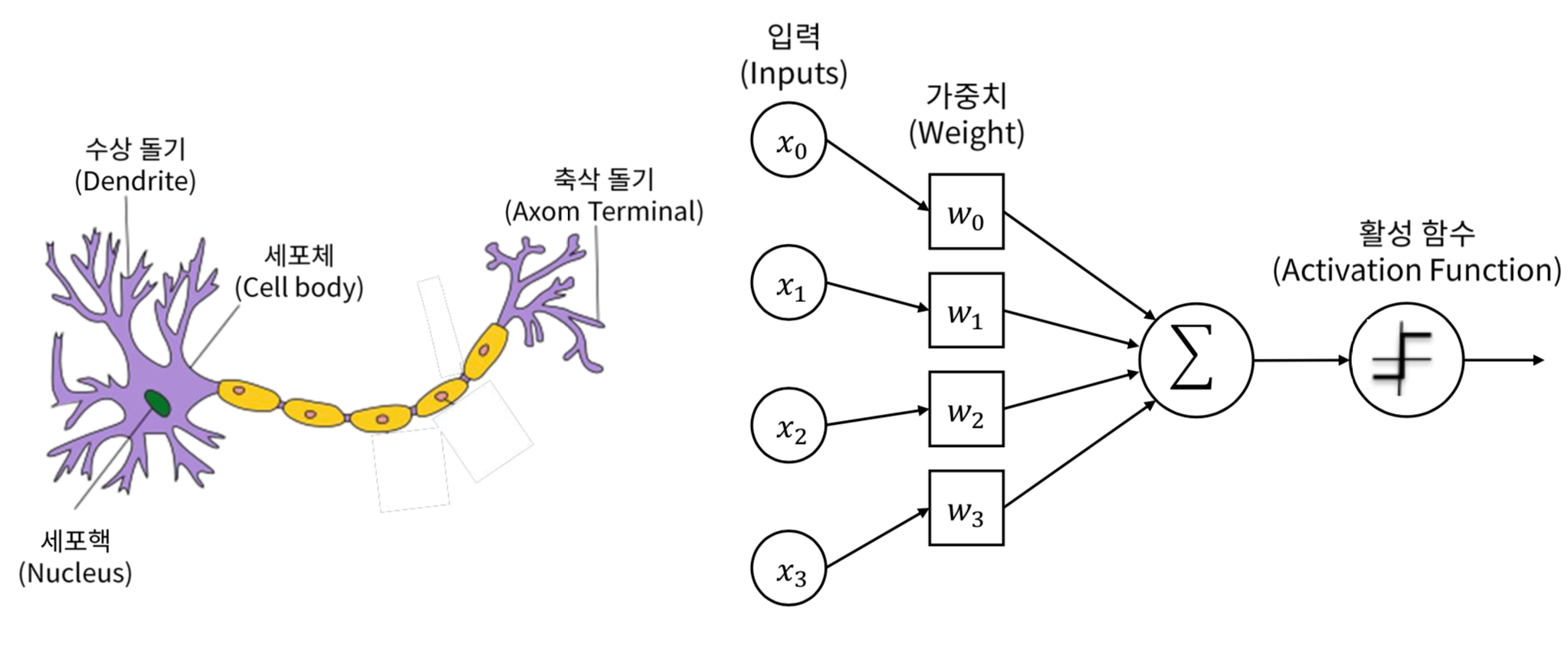
퍼셉트론의 구조는 입력층과 출력층이라는 2개의 층으로 구성되는 단순한 구조로 이루어집니다.

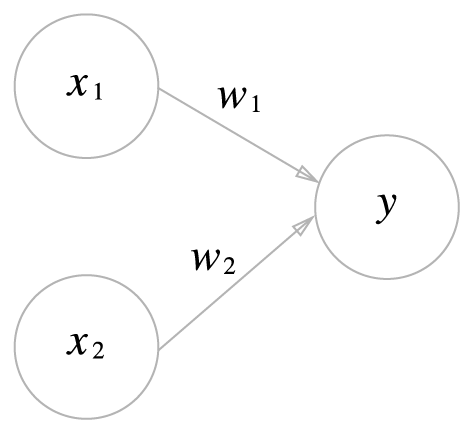
_images/fig2-1.png — 그림 2-1 입력이 2개인 퍼셉트론

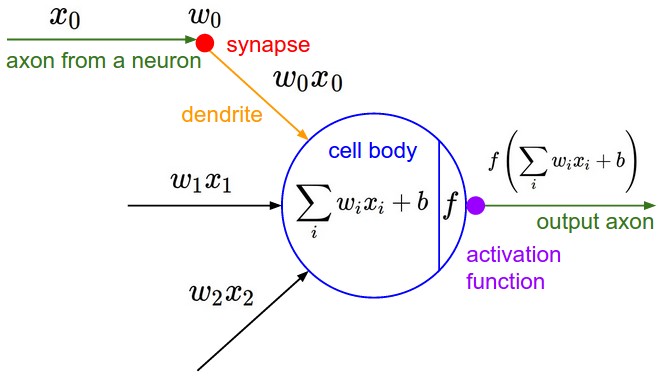
그림 2-1은 입력으로 2개의 신호를 받은 퍼셉트론의 예입니다. \(x_1\), \(x_2\)는 입력 신호, \(y\)는 출력신호, \(w_1\), \(w_2\)는 가중치 ^weight를 뜻합니다. 그림에서 원은 뉴런 혹은 노드라고 부릅니다.

2개 입력에 대한 퍼셉트론은 다음과 같은 수식으로 나타낼 수 있습니다.

(1)\[\begin{split}y = \begin{cases} 0, & \text{if} \quad w_1 x_1 + w_2 x_2 <= \beta \\ 1, & \text{if} \quad w_1 x_1 + w_2 x_2 > \beta \end{cases}\end{split}\]

더 일반적으로 \(d\) 개의 입력을 가지는 퍼셉트론은 다음과 같이 나타낼 수 있습니다.

\[\begin{split}y = \tau(w_1 x_1 + w_2 x_2 + \cdots + w_d x_d) \\ \tau(a) = \begin{cases} 0, & \text{if} \quad a <= \beta \\ 1, & \text{if} \quad a > \beta \end{cases}\end{split}\]

여기서 \(a = w_1 x_1 + w_2 x_2 + \cdots + w_d x_d\)입니다. 다음은 \(d=2\)일 때 예를 들어서 설명합니다.

단순한 논리연산

퍼셉트론을 활용한 간단한 문제를 살펴봅니다. 첫번째로 논리곱(AND) 진리표를 살펴봅니다. 두 입력이 모두 1일 때만 1을 출력하고 그 외에는 0을 출력합니다.

논리곱(AND 게이트)

논리곱
\(x_1\)	\(x_2\)	\(y\)
0	0	0
1	0	0
0	1	0
1	1	1

위 표를 퍼셉트론으로 표현한다는 것은 \(w_1, w_2, \beta\)를 결정하는 것입니다. 위 조건을 만족하는 매개변수 조합은 무수히 많습니다. 가령 \((w_1, w_2, \beta) = (0.5, 0.5, 0.5)\)로 하거나 \((0.5, 0.5, 0.8)\)로 하는 등 무수히 많은 조합을 찾을 수 있습니다.

부정 논리곱(NAND 게이트)

NAND는 not and를 의미하며 AND의 출력을 부정한 것이 됩니다.

부정 논리곱
\(x_1\)	\(x_2\)	\(y\)
0	0	1
1	0	1
0	1	1
1	1	0

NAND 게이트를 표현하는 방법은 무수히 많지만, 예를 들어 \((w_1, w_2, \beta) = (-0.5, -0.5, -0.7)\)의 조합이 있을 수 있습니다.

논리합(OR 게이트)

논리합
\(x_1\)	\(x_2\)	\(y\)
0	0	0
1	0	1
0	1	1
1	1	1

단순한 논리 퍼셉트론 구현

간단한 구현

다음은 논리곱(AND 게이트)를 구현한 것입니다. \(x_1\), \(x_2\)를 입력받아 결과를 반환합니다.

In [1]: def AND(x1, x2):
   ...:   w1, w2, beta = 0.5, 0.5, 0.7
   ...:   tmp = x1 * w1 + x2 * w2
   ...:   if tmp <= beta:
   ...:     return 0
   ...:   elif tmp > beta:
   ...:     return 1
   ...: 

In [2]: print("AND(0, 0)={}, AND(1, 0)={}, AND(0, 1)={}, AND(1, 1)={}".format(AND(0, 0), AND(1, 0), AND(0, 1), AND(1, 1)))
AND(0, 0)=0, AND(1, 0)=0, AND(0, 1)=0, AND(1, 1)=1

직접하기

NAND 게이트를 파이썬 함수로 구현해서 확인 해보세요. 여기서 \(w_1 = w_2 = -0.5\), \(\beta = -0.7\)을 사용해보고 가능한 다른 값들은 무엇이 있는지 생각해보세요.
OR 게이트를 구현하기 위해 필요한 \(w_1, w_2, \beta\)을 결정하고 OR 함수를 작성 하세요.

벡터 표현

퍼셉트론을 다르게 표현하면 다음과 같습니다. 식 (1)에서 \(-\beta\)를 \(b\)로 표현한 것입니다.

\[\begin{split}y = \begin{cases} 0, & \text{if} \quad w_1 x_1 + w_2 x_2 + b <= 0 \\ 1, & \text{if} \quad w_1 x_1 + w_2 x_2 + b > 0 \end{cases}\end{split}\]

여기서 \(b\)는 입력 \(x_1, x_2\)이 모두 0일 때 퍼셉트론이 0으로부터 벗어난 정도를 나타낸다고 편향^bias 이라고 합니다.

단순한 논리연산 퍼셉트론을 좌표평면 위에 기하적으로 표현하면 4개의 점을 분리하는 직선의 방정식을 찾는 문제와 같습니다. 이 직선은 벡터 \(\mathbf{w} = (w_1, w_2)\)에 수직인 직선이 됩니다.

또한 다음과 같이 3차원 공간 \((x, y, z)\)에서 표현하면 4점을 분리하는 평면의 방정식을 찾는 것과 같다고 할 수 있습니다.

\[z = w_1 x + w_2 y + b\]

\(z\)가 0보다 작거나 같으면 0을 반환하고 그렇지 않으면 1을 반환하는 알고리즘입니다. 즉 공간의 점 \((x,y,z)\)이 \(xy\) 평면 아래 있는 것과 위에 있는 것으로 분리하는 것과 마찬가지입니다.

넘파이를 이용해서 구현을 해봅니다.

In [5]: import numpy as np
   ...: x = np.array([0, 1])
   ...: w = np.array([0.5, 0.5])
   ...: b = -0.7
   ...: print(w * x)
   ...: print(np.sum(w * x))
   ...: print(np.sum(w * x) + b)
   ...: 
[0.  0.5]
0.5
-0.19999999999999996

두 벡터 \(w = (w_1, w_2)\), \(x = (x_1, x_2)\)의 성분끼리 곱 w * x을 한 후 b를 더하여 구한 것입니다.

이것을 이용해서 AND 게이트를 다시 구현해봅니다.

In [6]: def AND(x1, x2):
   ...:   x = np.array([x1, x2])
   ...:   w = np.array([0.5, 0.5])
   ...:   b = -0.7
   ...:   tmp = np.sum(w * x) + b
   ...:   if tmp <= 0:
   ...:     return 0
   ...:   elif tmp > 0:
   ...:     return 1
   ...: 

\(w_1, w_2\)는 입력 신호가 결과에 주는 영향력(중요도)을 조절하는 매개변수이고 편향은 뉴런이 얼마나 쉽게 활성화하느냐를 조정하는 매개변수입니다. 예를 들어 b가 -0.1이면 각 입력 신호에 가중치를 곱한 값들이 0.1을 초과할 때만 뉴런이 활성화됩니다. 반면 b가 -20.0이면 각 입력신호에 가중치를 곱한 값들의 합이 20.0을 넘지 않으면 뉴런은 활성화되지 않습니다. 이처럼 편향의 값은 뉴런(노드)이 얼마나 쉽게 활성화되는지를 결정합니다.

직접하기

NAND 게이트를 넘파이 배열을 이용해서 구현하고 테스트 해보세요. \(w_1 = w_2 = -0.5\), \(b = 0.7\)을 사용하세요.
OR 게이트를 넘파이 배열을 이용해서 구현하기 위한 \(w_1, w_2, b\)을 결정하고 OR 함수를 작성해서 확인해보세요.

퍼셉트론 학습 알고리즘

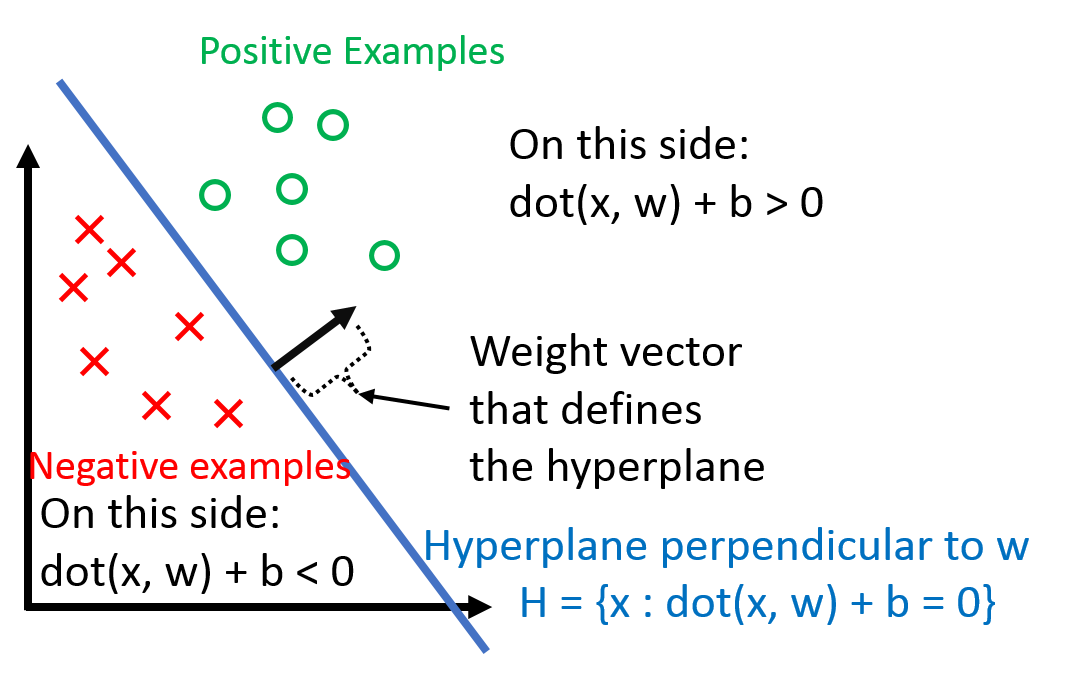
_images/perceptron_img1.png — 출처: 퍼셉트론 분류

퍼셉트론 의사 알고리즘

_images/perceptron_algo.png — 출처: 퍼셉트론 의사 알고리즘

기하적 직관

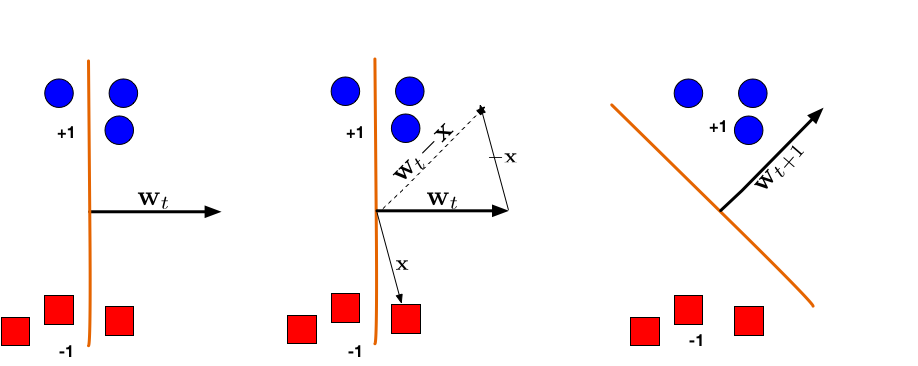
_images/PerceptronUpdate.png — 출처: 퍼셉트론 업데이트

(왼쪽) \(\mathbf{w}_t\) 에 의해 만들어진 초평면은 빨간 점과 파란 점 하나씩을 잘못 분류하고 있습니다. (중간) 빨간 점 \(\mathbf{x}\) 를 선택하여 업데이트를 진행합니다. 빨간색은 음수 (-1)로 분류되었기 때문에 \(\mathbf{w}_t\) 에서 \(\mathbf{x}\) 를 뺍니다. (오른쪽) 업데이트 된 초평면 \(\mathbf{w}_{t+1} = \mathbf{w}_t - \mathbf{x}\) 는 두 개의 부류로 분류가 됩니다.

퍼셉트론 학습 알고리즘 수렴 증명 2 

데이터 집합이 두 부류로(즉, \(y_i \in \{-1, +1\}\) ) 선형 분리가능하면 유한번 업데이트를 해서 분리 가능한 초평면 ^hyperplane을 찾을 수 있습니다.

분리가능하다는 가정에 의해서 모든 \((\mathbf{x}_i , y_i) \in D\)에 대해서 \(y_i(\mathbf{x}^T \mathbf{w}^{\ast}) > 0\)를 만족하는 초평면 \(\mathbf{w}^{\ast}\) 이 존재한다는 가정을 합니다. 여기서 \(\mathbf{x}^T \mathbf{w}^\ast = \mathbf{x} \cdot \mathbf{w}^\ast\)를 의미하므로 이것의 부호로 \(\mathbf{x}\) 가 \(\mathbf{w}^\ast\) 와 같은 방향인지를 측정할 수 있습니다.

계산의 편의를 위해 각 데이터 \(\mathbf{x}_i\)를 단위구 내부로 조정하고(가장 큰 벡터의 크기로 나눕니다), \(\mathbf{w}^{\ast}\) 는 단위 벡터를 만족한다고 가정합니다. 즉,

\[\| \mathbf{w}^{\ast} \| = 1 \quad \text{이고} \quad \| \mathbf{x}_i \| \le 1 \quad \forall \mathbf{x}_i \in D\]

초평면과 가장 짧은 거리인 \(\gamma = \min_{(\mathbf{x}_i, y_i) \in D} |\mathbf{x}_i^T \mathbf{w}^{\ast}|\) 를 정의합니다. \(\gamma\)가 초평면과의 가장 작은 거리가 되는 이유는 단위벡터 \(\mathbf{w}^{\ast}\) 와 어떤 벡터와 내적한 값의 절대값은 단위벡터에 정사영된 벡터의 크기이기 때문입니다.

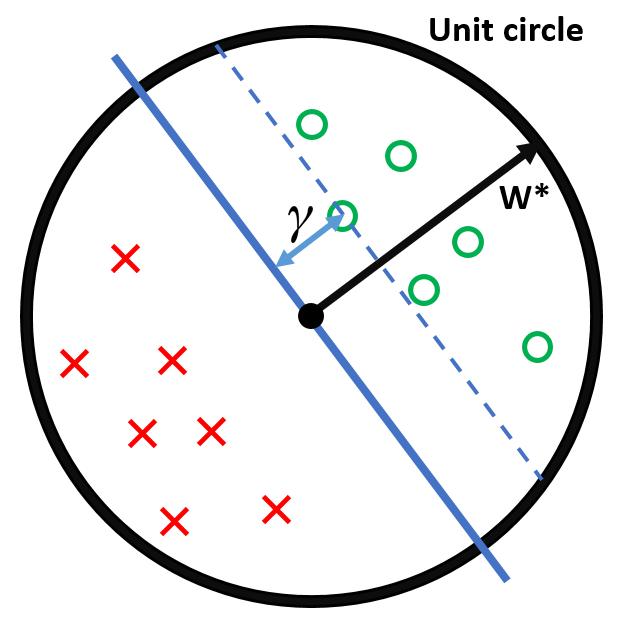
정리하면 다음과 같습니다.

모든 입력 \(\mathbf{x}_i\) 는 단위구 안에 있습니다.
\(\| \mathbf{w}^{\ast} \| = 1\) 을 만족하는 초평면 \(\mathbf{w}^{\ast}\) 가 존재합니다.
\(\gamma\) 는 초평면으로부터 가장 가까운 데이터 까지의 거리입니다.

정리: 위 조건을 만족하면, 퍼셉트론 학습 알고리즘은 \(1/\gamma^2\) 번 업데이트 안에 데이터를 분리하는 초평면을 찾을 수 있습니다.

증명:

\(\mathbf{w}^T \mathbf{w}^{\ast}\) 와 \(\mathbf{w}^T \mathbf{w}\) 의 성질을 관찰함으로 증명을 합니다. 퍼셉트론 학습 알고리즘에 의해서 \(\mathbf{w}\) 는 \(\mathbf{w} + y\mathbf{x}\)로 업데이트가 됩니다. 여기서 \(y = \pm 1\) 입니다. 다음 두 가지 사실을 이용합니다.

\(y(\mathbf{x}^T \mathbf{w}) \le 0\): \(\mathbf{x}\) 는 \(\mathbf{w}\) 에 의해서 잘못 분류되었으므로 이 경우에 업데이트를 진행합니다.
\(y(\mathbf{x}^T \mathbf{w}^{\ast}) > 0\): 모든 데이터는 \(\mathbf{w}^{\ast}\)에 의해서 올바르게 분류된다고 간주합니다.

\(\mathbf{w}^T \mathbf{w}^{\ast}\) 에 대한 업데이트

\[(\mathbf{w} + y \mathbf{x})^T \mathbf{w}^{\ast} = \mathbf{w}^T \mathbf{w}^{\ast} + y(\mathbf{x}^T \mathbf{w}^{\ast}) \ge \mathbf{w}^T \mathbf{w}^{\ast} + \gamma\]

왜냐면 \(y(\mathbf{x}^T \mathbf{w}^{\ast}) = |\mathbf{x}^T \mathbf{w}^{\ast}| \ge \gamma\) 이기 때문입니다.

이것으로부터 \(\mathbf{w}^T \mathbf{w}^{\ast}\) 업데이트는 이전보다 적어도 \(\gamma\) 보다 크거나 같은 양만큼 커집니다.
\(\mathbf{w}^T \mathbf{w}\) 에 대한 업데이트

\[(\mathbf{w} + y \mathbf{x})^T (\mathbf{w} + y \mathbf{x}) = \mathbf{w}^T \mathbf{w} + 2y(\mathbf{w}^T \mathbf{x}) + y^2 (\mathbf{x}^T \mathbf{x}) \le \mathbf{w}^T \mathbf{w} + 1\]
- \(2y(\mathbf{w}^T \mathbf{x}) < 0\) 입니다. 왜냐면 \(\mathbf{x}\)는 잘못된 분류였기 때문에 업데이트를 했기 때문입니다.
- \(0 \le y^2 (\mathbf{x}^T \mathbf{x}) \le 1\) 입니다. 왜냐면 \(y^2 = 1\) 이고 \(\| \mathbf{x} \| \le 1\) 이기 때문입니다.
이것으로부터 \(\mathbf{w}^T \mathbf{w}\) 업데이트는 이전보다 1보다 작거나 같은 양만큼 커집니다.
\(M\) 번 업데이트를 한 후에는 다음 식이 만족됩니다.
1. \(\mathbf{w}^T \mathbf{w}^{\ast} \ge M \gamma\)
2. \(\mathbf{w}^T \mathbf{w} \le M\)
따라서 다음과 같이 증명이 완성됩니다.

\[\begin{split}M \gamma & \le \mathbf{w}^T \mathbf{w}^\ast & \quad \text{(a)에 의해} \\ & = \| \mathbf{w} \| \cos (\theta) & \quad \text{내적} \\ & \le \| \mathbf{w} \| \\ & = \sqrt{\mathbf{w}^T \mathbf{w}} \\ & \le \sqrt{M} & \quad \text{(b)에 의해} \\ \\ \\ & \Rightarrow M \gamma \le \sqrt{M} \\ & \Rightarrow M^2 \gamma^2 \le M \\ & \Rightarrow M \le \frac{1}{\gamma^2}\end{split}\]

다층 퍼셉트론

앞에서 봤던 퍼셉트론은 선형분리 가능한 문제에만 작동을 합니다. 다음과 같은 XOR 게이트 연산을 푸는데 사용할 수 없습니다.

XOR 게이트

XOR 게이트는 배타적 논리합(exclusive or)이라는 연산입니다.

XOR 게이트
\(x_1\)	\(x_2\)	\(y\)
0	0	0
1	0	1
0	1	1
1	1	0

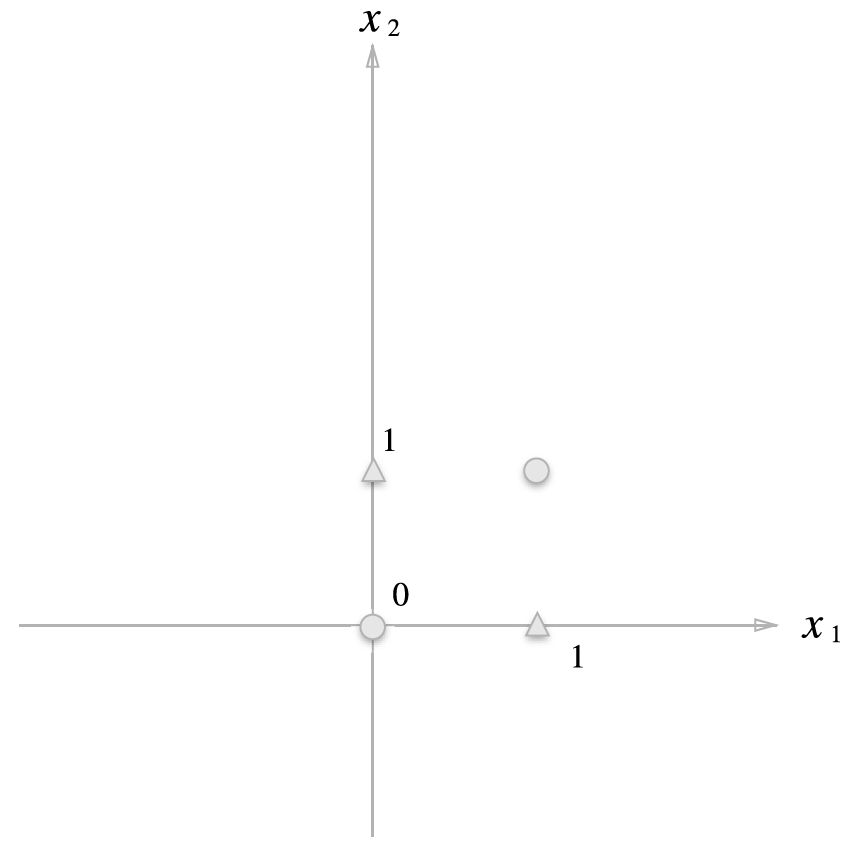
앞에서 봤던 퍼셉트론은 좌표 평면에서 직선으로 분리하는 방법이었습니다. 그러나 XOR 게이트는 어떤 직선으로도 세모와 동그라미를 분리할 수 없는 것을 알 수 있습니다. 따라서 퍼셉트론으로는 해결할 수 없는 문제가 됩니다.

하지만 퍼셉트론을 한 층 더 쌓으면 이 문제를 해결할 수 있습니다. 우선 논리 게이트 표시에 대해 알아봅니다.

어떤 조합을 하면 XOR 게이트를 표현할 수 있을지를 생각해봅니다.

NAND, OR, AND를 다음과 같이 조합하면 XOR 게이트를 완성할 수 있습니다.

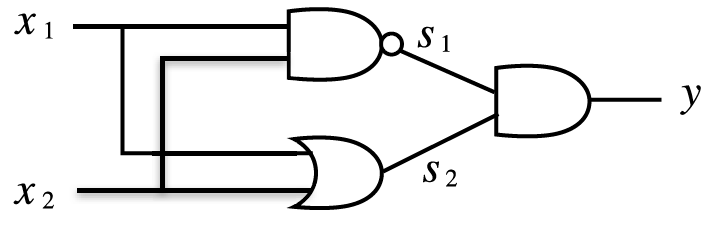
이것을 진리표로 나타내면 다음과 같습니다.

XOR(2층 퍼셉트론)
\(x_1\)	\(x_2\)	\(s_1(x_1\text{NAND}x_2)\)	\(s_2(x_1\text{OR}x_2)\)	\(y(s_1\text{AND}s_2)\)
0	0	1	0	0
1	0	1	1	1
0	1	1	1	1
1	1	0	1	0

XOR 게이트 구현

In [7]: def XOR(x1, x2):
   ...:   s1 = NAND(x1, x2)
   ...:   s2 = OR(x1, x2)
   ...:   y = AND(s1, s2)
   ...:   return y
   ...: 

실행해보면 다음과 같이 맞게 출력되는 것을 볼 수 있습니다.

In [8]: print(XOR(0, 0))
   ...: print(XOR(1, 0))
   ...: print(XOR(0, 1))
   ...: print(XOR(1, 1))
   ...: 
0
1
1
0

그림으로 나타내면 다음과 같습니다.

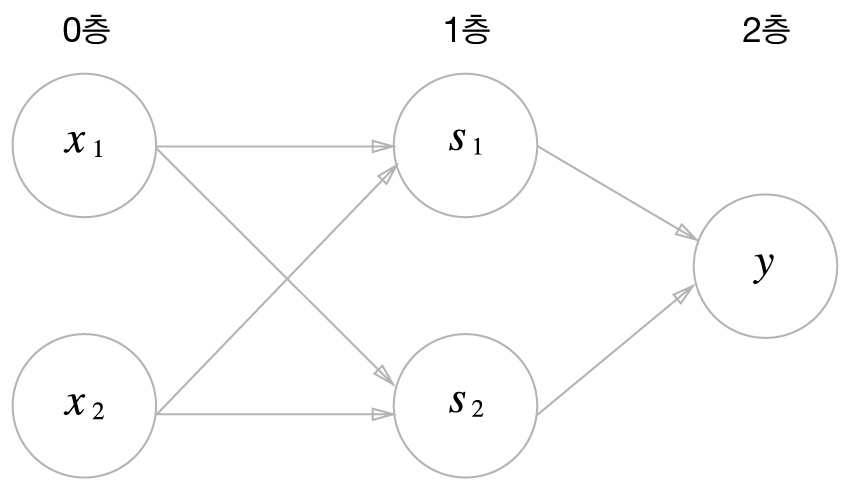
\(x_1, x_2\)를 입력층, NAND, OR 계산이 1층, AND 계산을 2층이라고 하며 다층 퍼셉트론이라고 합니다.

참조

1: https://www.simplilearn.com/tutorials/deep-learning-tutorial/perceptron
2: https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote03.html

연습문제

다음 표를 만족하는 퍼셉트론을 구현해 보세요. 즉, 다음 식을 만족하는 \(w_1, w_2, b\)를 구해서 파이썬 함수로 만들어 보세요.

\[\begin{split}y = \begin{cases} 0, & \text{if} \quad w_1 x_1 + w_2 x_2 + b <= 0 \\ 1, & \text{if} \quad w_1 x_1 + w_2 x_2 + b > 0 \end{cases}\end{split}\]

\(x_1\)

\(x_2\)

\(y\)

0

0

0

-1

0

1

-1

1

1

0

1

1
다음 표를 만족하는 퍼셉트론을 구현해 보세요. 즉, 다음 식을 만족하는 \(w_1, w_2, b\)를 구해서 파이썬 함수로 만들어 보세요.

\[\begin{split}y = \begin{cases} 0, & \text{if} \quad w_1 x_1 + w_2 x_2 + b <= 0 \\ 1, & \text{if} \quad w_1 x_1 + w_2 x_2 + b > 0 \end{cases}\end{split}\]

\(x_1\)

\(x_2\)

\(y\)

-1

-1

0

-1

1

1

1

-1

1

1

1

1
다음 표를 만족하는 퍼셉트론이 가능한지를 판단하고, 가능하다면 다음 식을 만족하는 \(w_1, w_2, b\)를 구해서 파이썬 함수로 만들어 보세요.

\[\begin{split}y = \begin{cases} -1, & \text{if} \quad w_1 x_1 + w_2 x_2 + b <= 1 \\ 1, & \text{if} \quad w_1 x_1 + w_2 x_2 + b > 1 \end{cases}\end{split}\]

\(x_1\)

\(x_2\)

\(y\)

0.3

0.6

-1

0.5

0.1

1

0.7

2

1

1.2

0.5

1
퍼셉트론 의사 알고리즘을 구현하세요.