파이썬 기초¶
기본 문법¶
산술연산¶
사칙연산은 다음과 같이 할 수 있습니다.
In [1]: 2 + 3
Out[1]: 5
In [2]: 1 - 2
Out[2]: -1
나눗셈은 실수값이 나옵니다.
In [3]: 2 / 3
Out[3]: 0.6666666666666666
거듭제곱은 별표 2개를 이어서 **을 사용합니다.
In [4]: 2 ** 3
Out[4]: 8
자료형¶
프로그래밍 언어에는 자료형이 있습니다. 자료형이란 데이터의 성질을 나타내는 것으로 파이썬에서는 type() 함수를 이용해서 자료형을 알 수 있습니다.
숫자 100은 정수(int)형입니다.
In [5]: type(100)
Out[5]: int
소수점이 들어간 숫자열은 실수형(float) 또는 부동소수점형이라고 합니다.
In [6]: type(1.234)
Out[6]: float
작은 따옴표 ‘ 사이에 있는 모든 문자들은 문자열(str)형입니다.
In [7]: type('안녕하세요')
Out[7]: str
변수¶
알파벳 또는 한글들을 사용하여 변수를 정의할 수 있습니다. 변수를 이용하여 값을 담거나 계산하는데 사용합니다.
In [8]: x = 100
...: print(x)
...:
100
같은 변수에는 가장 최근의 값이 저장됩니다.
In [9]: x = 10
...: print(x)
...:
10
연산을 하는데 사용될 수 있습니다.
In [10]: y = 20.3
....: x * y
....:
Out[10]: 203.0
정수형 x와 실수형 y의 곱이 실수형이 되는 것을 알 수 있습니다. 자동형변환이 일어납니다.
In [11]: type(x * y)
Out[11]: float
리스트¶
파이썬은 데이터를 저장할 수 있는 리스트(list)를 제공합니다. 리스트는 대괄호 [] 사이에 자료를 쉼표로 구분해서 만듭니다.
In [13]: a = [1, 2, 3, 4, 5]
첫번째 성분을 접근하기 위해서는 인덱스 0을 사용합니다. 인덱스(index)란 리스트에서 성분의 위치를 표시하는 0부터 시작하는 정수를 말합니다. 첫번째 성분을 가리키는 인덱스는 파이썬에서는 0입니다.
In [14]: a[0]
Out[14]: 1
5번째 성분에 접근은 다음과 같이 합니다.
In [15]: a[4]
Out[15]: 5
인덱스에 음수를 사용하면 끝에서부터 위치를 의미합니다. 따라서 마지막 성분은 다음과 같이 구할 수도 있습니다.
In [16]: a[-1]
Out[16]: 5
리스트 성분의 개수는 len() 함수를 이용합니다.
In [17]: len(a)
Out[17]: 5
리스트 성분을 변경하려면 다음과 같이 합니다.
In [18]: a[1] = -10.4
....: print(a)
....:
[1, -10.4, 3, 4, 5]
리스트의 연속적인 부분 성분들을 접근하기 위해서는 슬라이싱(slicing)을 이용할 수 있습니다. 슬라이싱은 시작 인덱스와 끝 인덱스를 콜론을 이용해서 적습니다.
주의해야 할 것은 끝 인덱스는 포함되지 않는다는 것입니다.
In [19]: a[1:4]
Out[19]: [-10.4, 3, 4]
끝을 나타내는 인덱스를 생략하면 끝까지를 의미합니다. 1번 인덱스부터 끝까지는 다음과 같습니다.
In [20]: a[1:]
Out[20]: [-10.4, 3, 4, 5]
시작 인덱스를 생략하면 처음부터 시작합니다. 다음은 처음부터 인덱스 2까지 나타냅니다.
In [21]: a[:3]
Out[21]: [1, -10.4, 3]
처음부터 마지막까지는 다음과 같이 음수 인덱스를 사용하여 나타낼 수도 있습니다.
In [22]: a[:-1]
Out[22]: [1, -10.4, 3, 4]
딕셔너리(dictionary)¶
데이터를 저장하는 다른 방법으로 딕셔너리가 있습니다. 이것은 키(key)와 값(value) 쌍으로 이루어 집니다. 키를 통해서 값을 접근하고 수정할 수 있습니다.
중괄호 {} 사이에 콜론을 이용하여 키:값 형식으로 저장하고 쉼표를 이용하여 여러 개의 값을 저장할 수 있습니다.
In [23]: me = {'height': 170, 'age': 25}
값을 접근하려면 대괄호 안에 키를 이용합니다.
In [24]: me['height']
Out[24]: 170
새로운 성분을 추가하려면 다음과 같이 할 수도 있습니다.
In [25]: me['weight'] = 65
....: print(me)
....:
{'height': 170, 'age': 25, 'weight': 65}
bool¶
파이썬에서 참(True), 거짓(False)를 나타내는 bool 자료형이 있습니다. 논리 연산자인 and, or, not을 사용할 수있습니다.
In [26]: happy = True
....: sleepy = False
....: type(happy)
....:
Out[26]: bool
not을 이용하여 부정을 만들 수 있습니다.
In [27]: not happy
Out[27]: False
and를 이용하여 논리곱을 계산합니다.
In [28]: happy and sleepy
Out[28]: False
or를 이용하여 논리합을 계산합니다.
In [29]: happy or sleepy
Out[29]: True
if 문¶
조건을 처리하기 위해서 if-else 문을 사용합니다.
if 다음에 조건문이 나오고 콜론으로 라인을 마무리하고 다음 라인부터 같은 크기만큼 들여쓰기를 해서 블록을 만듭니다.
In [30]: happy = True
....: if happy:
....: print('지금 전 행복해요')
....:
지금 전 행복해요
else 문을 사용해서 조건이 거짓일 때 실행될 블록을 만듭니다.
In [31]: sleepy = False
....: if sleepy:
....: print('지금 전 졸려요')
....: else:
....: print('졸리지 않아요.')
....:
졸리지 않아요.
for 문¶
반복을 위해 for 문을 사용할 수 있습니다.
for 다음에 변수 이름이 나오고 in 다음에 리스트(반복가능 객체)가 나와 리스트에 있는 성분들 하나 하나가 차례로 변수에 대응되어 실행됩니다.
다음은 변수 이름이 i이고 리스트는 [1, 2, 3]으로 각 성분이 하나씩 출력이 됩니다.
In [32]: for i in [1, 2, 3]:
....: print(i)
....:
1
2
3
함수¶
특정한 기능을 수행하는 일련의 문장들을 묶어 재사용 가능하게 만드는 것이 함수입니다.
함수는 def 라는 식별자를 사용하여 만듭니다.
In [33]: def greet():
....: print('안녕하세요')
....:
함수를 실행할 때는 함수 이름과 소괄호를 이용하면됩니다.
In [34]: greet()
안녕하세요
함수는 인자를 정의하여 함수의 입력을 제어합니다.
In [35]: def greet(name):
....: print(name + '님. 안녕하세요.')
....:
함수를 호출할 때 인자를 넘겨줍니다.
In [36]: greet('지수')
지수님. 안녕하세요.
스크립트 파일¶
파이썬 프로그램을 파일로 저장하고 그 파일의 내용을 한꺼번에 차례로 실행할 수 있습니다. 이 파일을 파이썬 스크립트 파일이라 부르고 확장자는 .py를 붙입니다.
파일로 저장¶
텍스트 편집기를 열고 다음과 같은 내용을 입력하고 hello.py 파일에 저장합니다.
print('파이썬 스크립트 파일에서 실행됩니다.')
아나콘다 명령창에서 다음과 같이 입력해서 실행합니다.
python hello.py
클래스¶
파이썬은 int와 str등의 자료형을 가지고 있는 것을 살펴보았습니다. 사용자가 직접 자신만의 자료형을 만들어 사용할 수가 있습니다. 뿐만아니라 자료형의 메소드와 속성을 만들어 사용할 수도 있습니다. 자신만의 자료형은 클래스라고 합니다. 클래스는 class라는 키워드를 이용해서 정의합니다.
class 클래스이름:
def __init__(self, 인수, ...): # 생성자
...
def 메소드이름1(self, 인수, ...): # 메소드
...
def 메소드이름2 (self, 인수, ...): # 메소드
...
__init__ 메소드는 클래스 인스턴스 만들 때 자동으로 실행됩니다. 인스턴스는 클래스이름(인수, ...)과 같이 만듭니다.
다음은 Human 클래스를 만들어서 인스턴스를 만드는 예제입니다.
In [37]: class Human:
....: def __init__(self, name):
....: self.name = name
....: print("초기화되었습니다.")
....: def hello(self):
....: print("안녕하세요. " + self.name + "!")
....: def goodbye(self):
....: print("잘가요. " + self.name + "!")
....:
....: m = Human("지원")
....: m.hello()
....: m.goodbye()
....:
초기화되었습니다.
안녕하세요. 지원!
잘가요. 지원!
클래스의 인스턴스는 Human()과 같이 만듭니다. Human의 생성자(초기화 메서드)는 name이라는 인수를 받고, 그 인수로 인스턴스 변수인 self.name을 초기화합니다. 인스턴스 변수는 인스턴스별로 저장되는 변수입니다. 파이썬에서는 self.name처럼 self 다음에 속성 이름을 써서 인스턴스 변수를 작성하거나 접근할 수 있습니다. Human 클래스는 hello(), goodbye() 메소드를 가지고 있습니다. 메소드를 실행하려면 인스턴스 변수 바로 다음에 점 .을 찍고 메소드 이름을 쓰고 소괄호를 열고 닫으면 됩니다.
넘파이(Numpy)¶
딥러닝을 구현하다 보면 배열이나 행렬 계산이 많이 등장합니다. 넘파이의 배열 클래스인 numpy.array에는 편리한 메서드가 많이 준비되어 있어, 딥러닝을 구현할 때 이들 메서드를 이용합니다. 이번 절에서는 앞으로 사용할 넘파이에 대해서 간략히 설명합니다.
넘파이 가져오기¶
넘파이는 외부 라이브러리입니다. 여기서 말하는 ‘외부’는 표준 파이썬에는 포함되지 않는다는 것입니다. 그래서 우선 넘파이 라이브러리를 쓸 수 있도록 가져와야(import) 합니다.
In [38]: import numpy as np
파이썬에서는 라이브러리를 읽기 위해서 import 문을 이용합니다. 여기에서는 import numpy as np라고 썼는데, 직역하면 “numpy를 np라는 이름으로 가져오세요”가 됩니다. 이렇게 해두면 앞으로 넘파이가 제공하는 메서드를 np를 통해 참조할 수 있습니다.
넘파이 배열 생성하기¶
넘파이 배열을 만들 때는 np.array() 메서드를 이용합니다. np.array()는 파이썬의 리스트를 인수로 받아 넘파이 라이브러리가 제공하는 특수한 형태의 배열(numpy.ndarray)을 반환합니다.
In [39]: x = np.array([1.0, 2.0, 3.0])
....: print(x)
....: type(x)
....:
[1. 2. 3.]
Out[39]: numpy.ndarray
넘파이의 산술 연산¶
다음은 넘파이 배열로 산술 연산을 수행하는 예입니다.
>>> x = np.array([1.0, 2.0, 3.0])
>>> y = np.array([2.0, 4.0, 6.0])
>>> x + y # 원소별 덧셈
array([ 3., 6., 9.])
>>> x - y
array([ -1., -2., -3.])
>>> x * y # 원소별 곱셈
array([ 2., 8., 18.])
>>> x / y
array([ 0.5, 0.5, 0.5])
여기에서 주의할 점은 배열 x와 y의 원소 수가 같다는 것입니다(둘 다 원소를 3개씩 갖는 1차원 배열). x와 y의 원소 수가 같다면 산술 연산은 각 원소에 대해서 행해집니다. 원소 수가 다르면 오류가 발생하니 원소 수 맞추기는 중요하답니다. 참고로, ‘원소별’이라는 말은 영어로 element-wise라고 합니다. 예컨대 ‘원소별 곱셈’은 element-wise product라고 합니다.
넘파이 배열은 원소별 계산뿐 아니라 넘파이 배열과 수치 하나(스칼라값)의 조합으로 된 산술 연산도 수행할 수 있습니다. 이 경우 스칼라값과의 계산이 넘파이 배열의 원소별로 한 번씩 수행됩니다. 이 기능을 브로드캐스트라고 합니다(자세한 것은 브로드캐스트 절에서 설명하겠습니다).
>>> x = np.array([1.0, 2.0, 3.0])
>>> x / 2.0
array([ 0.5, 1., 1.5])
넘파이의 N차원 배열¶
넘파이는 1차원 배열(1줄로 늘어선 배열)뿐 아니라 다차원 배열도 작성할 수 있습니다. 예를 들어 2차원 배열(행렬)은 다음처럼 작성합니다.
>>> A = np.array([[1, 2], [3, 4]])
>>> print(A)
[[1 2]
[3 4]]
>>> A.shape
(2, 2)
>>> A.dtype
dtype('int64')
방금 2×2의 A라는 행렬을 작성했습니다. 행렬의 크기은 shape으로, 행렬에 담긴 원소의 자료형은 dtype으로 알 수 있습니다. 이어서 행렬의 산술 연산을 봅시다.
이 책에서는 행렬을 포함한 N차원 배열에서 그 배열의 ‘각 차원의 크기(원소 수)’를 배열의 ‘크기’라 하겠습니다.
>>> B = np.array([[3, 0], [0, 6]])
>>> A + B
array([[ 4, 2],
[ 3, 10]])
>>> A * B
array([[ 3, 0],
[ 0, 24]])
크기가 같은 행렬끼리면 행렬의 산술 연산도 대응하는 원소별로 계산됩니다. 배열과 마찬가지로 말이죠. 행렬과 스칼라값의 산술 연산도 가능합니다. 이때도 배열과 마찬가지로 브로드캐스트 기능이 작동합니다.
>>> print(A)
[[1 2]
[3 4]]
>>> A * 10
array([[ 10, 20],
[ 30, 40]])
Note
넘파이 배열(np.array)은 N차원 배열을 작성할 수 있습니다. 1차원 배열, 2차원 배열, 3차원 배열처럼 원하는 차수의 배열을 만들 수 있다는 뜻입니다. 수학에서는 1차원 배열은 벡터(vector), 2차원 배열은 행렬(matrix)이라고 부릅니다. 또 벡터와 행렬을 일반화한 것을 텐서(tensor)라 합니다. 여기서는 기본적으로 2차원 배열을 행렬, 3차원 이상의 배열을 다차원 배열이라 하겠습니다.
원소 접근¶
원소의 인덱스는 0부터 시작합니다. 그리고 각 원소에 접근하려면 다음과 같이 합니다.
In [40]: X = np.array([[51, 55], [14, 19], [0, 4]])
....: print(X)
....:
[[51 55]
[14 19]
[ 0 4]]
In [41]: X[0] # 0행
Out[41]: array([51, 55])
In [42]: X[0][1] # (0, 1) 위치의 원소
Out[42]: 55
In [43]: X[0, 1] # (0, 1) 위치의 원소
Out[43]: 55
for 문으로도 각 원소에 접근할 수 있습니다.
>>> for row in X:
... print(row)
...
[51 55]
[14 19]
[0 4]
넘파이는 지금까지의 방법 외에도, 인덱스를 배열로 지정해 한 번에 여러 원소에 접근할 수도 있습니다.
>>> X = X.flatten() # X를 1차원 배열로 변환(평탄화)
>>> print(X)
[51 55 14 19 0 4]
>>> X[np.array([0, 2, 4])] # 인덱스가 0, 2, 4인 원소 얻기
array([51, 14, 0])
이 기법을 응용하면 특정 조건을 만족하는 원소만 얻을 수 있습니다. 예컨대 다음과 같이 배열 X에서 15 이상인 값만 구할 수 있습니다.
>>> X > 15
array([ True, True, False, True, False, False], dtype = bool)
>>> X[X>15]
array([51, 55, 19])
넘파이 배열에 부등호 연산자를 사용한(앞 예에서 X>15) 결과는 bool 배열입니다. 여기에서는 이 bool 배열을 사용해 배열 X에서 True에 해당하는 원소, 즉 값이 15보다 큰 원소만 꺼내고 있습니다.
Note
파이썬 같은 동적 언어는 C나 C++ 같은 정적 언어(컴파일 언어)보다 처리 속도가 늦다고 합니다. 실제로 무거운 작업을 할 때는 C/C++로 작성한 프로그램을 쓰는 편이 좋습니다. 그래서 파이썬에서 빠른 성능이 요구될 경우 해당 부분을 C/C++로 구현하곤 합니다. 그때 파이썬은 C/C++로 쓰인 프로그램을 호출해주는, 이른바 ‘중개자’ 같은 역할을 합니다. 넘파이도 주된 처리는 C와 C++로 구현했습니다. 그래서 성능을 해치지 않으면서 파이썬의 편리한 문법을 사용할 수 있는 것입니다.
배열 형태 변경(reshape)¶
reshape 함수를 이용하면 배열의 형태를 변경할 수 있습니다.
In [44]: import numpy as np
....: a = np.arange(12).reshape((3, 4))
....: print(a)
....:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
order = ['C' | 'F']옵션을 이용해 행우선('C')으로 할 건지 열우선('F')할 건지를 선택할 수 있습니다. 'C'는 C 스타일, 'F'는 포트란 스타일입니다. C 스타일은 마지막 인덱스를 가장 먼저 읽고/쓰고 맨 처음 인덱스를 맨 나중에 읽고/씁니다. 기본 설정은 C 입니다.
예를 들어 2 x 3 x 2 형태의 배열 a 가 있을 때 a[i, j, k]에서 \(0 \le i <2\), \(0 \le j < 3\), \(0 \le k < 2\)의 범위를 움직입니다.
In [45]: a = np.arange(12).reshape((2, 3, 2), order = 'C')
....: print(a)
....:
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]]
C 스타일
위 배열을 C 스타일 1차원 배열로 읽고 써보겠습니다.
In [46]: a.reshape(-1, order='C')
Out[46]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
여기서 -1은 -1이 위치한 축을 제외한 나머지 축의 원소들의 갯수로 배열 a의 원소 갯수를 나눈 수의 크기를 갖는다는 의미입니다. 여기서는 -1은 0 축이고 나머지 축이 없고 배열 a의 크기는 12 이므로 0 축이 12개의 원소로 이루어지는 벡터 형식의 배열이 만들어집니다.
C 스타일은 읽고 쓸때 맨 끝에 있는 인덱스 k 가 먼저 변하기 시작합니다. 다음은 j가 하나씩 커지고 마지막으로는 맨 처음 인덱스 i가 커지게 되는 것입니다.
[0, 0, 0] -> [0, 0, 1] -> [0, 1, 0] -> [0, 1, 1] -> [0, 2, 0] -> [0, 2, 1] ->
(0) (1) (2) (3) (4) (5)
[1, 0, 0] -> [1, 0, 1] -> [1, 1, 0] -> [1, 1, 1] -> [1, 2, 0] -> [1, 2, 1]
(6) (7) (8) (9) (10) (11)
위에서 대괄호 안의 숫자들은 [i, j, k] 인덱스이고 소괄호 안의 숫자는 인덱스에 대응되는 배열의 원소를 나타냅니다. 위 인덱스 증가 규칙은 진법의 크기가 하나씩 증가하는 규칙과 같은 것을 알 수 있습니다. 물론 각 자리수의 최대값은 다르지만 말입니다.
F 스타일
배열 a를 다시 쓰면 다음과 같습니다.
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]]
F 스타일로 읽고 쓴다면 맨 처음 인덱스 i가 먼저 증가하고, 다음으로 j, k 순서로 증가하게 됩니다.
[0, 0, 0] -> [1, 0, 0] -> [0, 1, 0] -> [1, 1, 0] -> [0, 2, 0] -> [1, 2, 0] ->
(0) (6) (2) (8) (4) (10)
[0, 0, 1] -> [1, 0, 1] -> [0, 1, 1] -> [1, 1, 1] -> [0, 2, 1] -> [1, 2, 1]
(1) (7) (3) (9) (5) (11)
In [47]: a.reshape(-1, order='F')
....:
Out[47]: array([ 0, 6, 2, 8, 4, 10, 1, 7, 3, 9, 5, 11])
읽을 때 뿐만아니라 쓸 때도 같은 규칙으로 쓰는 것을 알 수 있습니다. 다음은 2 x 6 형태의 배열로 만드는데 위에서 F 스타일로 읽은 것을 쓸 때는 [i, j] 인덱스에 쓰게 됩니다. 즉 다음과 같은 인덱스 순서대로 원소를 대입하는 것입니다.
[0, 0] -> [1, 0] -> [0, 1] -> [1, 1] -> [0, 2] -> [1, 2] ->
(0) (6) (2) (8) (4) (10)
[0, 3] -> [1, 3] -> [0, 4] -> [1, 4] -> [0, 5] -> [1, 5]
(1) (7) (3) (9) (5) (11)
따라서 다음과 같은 결과가 나오게 됩니다.
In [48]: a.reshape(2, -1, order='F')
....:
Out[48]:
array([[ 0, 2, 4, 1, 3, 5],
[ 6, 8, 10, 7, 9, 11]])
브로드캐스트¶
두 개의 ndarray 크기가 맞지 않을 때 작은 배열을 큰 배열의 크기에 맞춰 늘리는 것을 브로드캐스트라고 합니다. 브로드캐스트는 먼저 두 배열(ndarray)이 브로드캐스트 가능한 지를 판단합니다. 브로드캐스트 가능한 배열이면 브로드캐스트 규칙에 따라 브로드캐스트를 하고 그렇지않으면 예외를 발생시킵니다.
넘파이에서는 크기가 다른 배열끼리도 계산할 수 있습니다. 앞의 예에서는 2×2 행렬 A에 스칼라값 10을 곱했습니다. 이때 [그림 1-1]과 같이 10이라는 스칼라값이 2×2 행렬로 확대된 후 연산이 이뤄집니다. 이 똑똑한 기능을 브로드캐스트(broadcast)라고 합니다.

그림 1-1 브로드캐스트의 예 : 스칼라값인 10이 2×2 행렬로 확대됩니다.
다른 예를 살펴봅시다.
>>> A = np.array([[1, 2], [3, 4]])
>>> B = np.array([10, 20])
>>> A * B
array([[ 10, 40],
[ 30, 80]])
여기에서는 [그림 1-2]처럼 1차원 배열인 B가 ‘똑똑하게도’ 2차원 배열 A와 똑같은 크기으로 변형된 후 원소별 연산이 이뤄집니다.

그림 1-2 브로드캐스트의 예 2
이처럼 넘파이가 제공하는 브로드캐스트 기능 덕분에 크기가 다른 배열끼리의 연산을 스마트하게 할 수 있습니다.
브로드캐스트 가능한지 판단¶
브로드캐스트 가능한 두 배열이란, 두 배열의 크기를 끝에서부터 맞춰었을 때 같은 자리에 있는 숫자가 같든지 아니면 1이어야 합니다.
배열 A의 크기가 2 x 1 x 3 이고 배열 B의 크기가 3이면 브로드캐스트 가능한 배열들 입니다.
2 x 1 x 3
3
왜냐면 두 배열의 크기를 끝에서부터 맞추었을 때 같은 위치에 있는 값이 모두 3으로 같기 때문입니다. 하지만 2 x 1 x 3 배열과 5 x 2 배열은 브로드캐스트 가능하지 않습니다.
2 x 1 x 3
5 x 2
왜냐면 첫번째 배열의 크기의 끝자리가 3이고 두번째 배열의 크기가 2로서 다르기 때문에 가능하지 않습니다.
다음과 같은 크기의 두 배열은 브로드캐스팅 가능합니다.
2 x 1 x 3
5 x 1
배열의 크기가 다르지만 같은 위치에 있는 값이 각각 1을 포함하기 때문에 가능합니다.
브로드캐스트 하는 방법¶
브로드캐스트 가능한 배열이라면 맨 먼저 두 배열의 크기를 끝부터 맞춥니다. 그리고 축이 없는 부분은 1로 채웁니다. 예를 들면
2 x 1 x 3
5 x 1
에서 첫번째 배열은 3개의 축으로 이루어진 2 x 1 x 3형태를 갖고 두번째 배열은 5 x 1로 2개의 축을 가집니다. 따라서 0 축에 해당하는 크기를 1로 채웁니다.
2 x 1 x 3
1 x 5 x 1
뒤에서부터 크기가 1인 부분을 다른 배열의 크기에 맞춰 값을 복사하여 브로드캐스트를 합니다. 즉, 위에서 브로드캐스트하고 난 후의 크기는
2 x 5 x 3
이 됩니다.
예를 들어 설명하겠습니다. 다음과 같이 A의 크기가 2 x 1 x 3이고 B의 크기가 5 x 1인 배열이라고 합니다.
A = [[[0, 1, 2]],
[[3, 4, 5]]]
B = [[0],
[1],
[2],
[3],
[4]]
In [49]: A = np.arange(6).reshape(2, 1, 3)
....: A
....:
Out[49]:
array([[[0, 1, 2]],
[[3, 4, 5]]])
In [50]: B = np.arange(5).reshape(5, 1)
....: B
....:
Out[50]:
array([[0],
[1],
[2],
[3],
[4]])
그러면 브로드캐스팅 가능한 배열이 되고 두 배열의 크기를 2 x 5 x 3으로 늘리게 됩니다. 늘리는 방법은 뒷쪽 부분부터 시작해서 같은 값을 복사합니다. 먼저 A는 2 x 5 x 3으로 만들기 위해 1 x 3 배열을 5개 복사합니다.
A = [[[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2]],
[[3, 4, 5],
[3, 4, 5],
[3, 4, 5]
[3, 4, 5]
[3, 4, 5]]]
B 배열은 1 x 5 x 1 크기이므로 뒷부분 5 x 1 부분을 먼저 5 x 3으로 만듭니다. 따라서 5개의 값을 각각 3개씩 복사하여 만듭니다.
B = [[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3],
[4, 4, 4]]
다음은 2 x 5 x 3의 크기를 만들기 위해 5 x 3의 배열을 똑같이 2개 복사하여 2 x 5 x 3 배열을 만듭니다.
B = [[[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3],
[4, 4, 4]],
[[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3],
[4, 4, 4]]]
최종적으로 만들어진(브로드캐스팅된) 배열 A, B는 다음과 같습니다.
A = [[[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2]],
[[3, 4, 5],
[3, 4, 5],
[3, 4, 5]
[3, 4, 5]
[3, 4, 5]]]
B = [[[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3],
[4, 4, 4]],
[[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3],
[4, 4, 4]]]
따라서 A + B는 다음과 같이 됩니다.
In [51]: A + B
Out[51]:
array([[[0, 1, 2],
[1, 2, 3],
[2, 3, 4],
[3, 4, 5],
[4, 5, 6]],
[[3, 4, 5],
[4, 5, 6],
[5, 6, 7],
[6, 7, 8],
[7, 8, 9]]])
축(axis)¶
numpy ndarray arr[x, y, z] 일 때 x 인덱스는 axis=0, y 인덱스는 axis=1, z 인덱스는 axis=2 와 같이 구분합니다. 따라서 axis=0를 기준으로 연산을 한다는 것은 y, z 인덱스는 고정시키고 x 인덱스만 변한다는 뜻입니다.
In [52]: import numpy as np
....: arr = np.arange(12).reshape(2, 3, 2)
....: arr
....:
Out[52]:
array([[[ 0, 1],
[ 2, 3],
[ 4, 5]],
[[ 6, 7],
[ 8, 9],
[10, 11]]])
배열 arr을 0 축으로 더한다는 것은 0 축의 성분만 변하게 더한다는 것입니다.
[0, j, k] + [1, j, k]
In [53]: arr.sum(axis=0)
Out[53]:
array([[ 6, 8],
[10, 12],
[14, 16]])
그러면 첫번째 축부분이 사라지면서 차원이 한 차원 낮아진 3 x 2 형태의 배열이 만들어지게 됩니다.
배열 arr을 1 축으로 더한다는 것은 1 축의 성분만 변하게 더해서 결과적으로는 2 x 2 형태의 배열이 만들어 집니다.
[i, 0, k] + [i, 1, k] + [i, 2, k]
In [54]: arr.sum(axis=1)
Out[54]:
array([[ 6, 9],
[24, 27]])
배열 arr을 2 축으로 더한다는 것은 2 축의 성분만 변하게 더한다는 것입니다.
[i, j, 0] + [i, j, 1]
In [55]: arr.sum(axis=2)
Out[55]:
array([[ 1, 5, 9],
[13, 17, 21]])
직접하기
위의 예제에서 axis=1 로 더하기를 했을 때 결과를 계산하시오.
전치(transpose)¶
행렬의 전치는 행과 열의 인덱스를 변경하는 것입니다.
텐서의 경우 전치도 비슷합니다. 3차원 텐서를 예를 들어보겠습니다. 3차원 각 축의 차원이 M, N, O라고 하고 다음과 같이 표시하겠습니다.
A가 \(T_{MNO}\) 의 원소 \(A \in T_{MNO}\) 라고 할 때, 그리고 각각의 인덱스를 \(i, j, k\) 라고 하면 다음과 같이 쓸 수 있습니다.
여기서
를 만족합니다.
3차원 텐서의 전치의 종류는 \(3!\) 가지가 있습니다. 다음은 0, 1, 2 축을 1, 2, 0 순서의 축으로 전치를 한 것을 다음과 같이 나타내도록 하겠습니다.
그러면
와 같이 됩니다. \(A^{T(1,2,0)}\)의 인덱스 k 는 원래 \(A\)의 0 축이 되고, i 인덱스는 1 축, j 인덱스는 2 축이 되는 것입니다. 즉, 원래 0 축은 2 축, 1 축은 0 축, 2 축은 1 축으로 옮겨가는 것입니다.
예를 들어 설명합니다. 3차원 텐서 3 x 2 x 2크기의 A를 만듭니다. \(A\)는 \(M=3, N=2, O=2\) 인 텐서 \(A \in T_{322}\) 를 의미합니다.
In [56]: A = np.arange(1, 13).reshape(3, 2, 2)
....: A
....:
Out[56]:
array([[[ 1, 2],
[ 3, 4]],
[[ 5, 6],
[ 7, 8]],
[[ 9, 10],
[11, 12]]])
\(i, j, k\) 번째 원소는 \(A_{ijk}\) 와 같이 나타내고 \(0 \le i < 3\), \(0 \le j < 2\), \(0 \le k < 2\)를 만족합니다. 넘파이로는 다음과 같이 표현합니다.
A[i][j][k] # 또는 A[i, j, k]
예를 들면 \(A_{201}\) 은 다음과 같습니다.
In [57]: A[2, 0, 1]
Out[57]: 10
축 1, 2, 0 순서로 전치한 텐서를 \(B\)로 정의합니다. 즉,
이라고 표시할 수 있습니다.
In [58]: B = A.transpose(1, 2, 0)
....: B
....:
Out[58]:
array([[[ 1, 5, 9],
[ 2, 6, 10]],
[[ 3, 7, 11],
[ 4, 8, 12]]])
즉,
입니다. 따라서
이 되는 것입니다. 넘파이 배열의 성분이 다음과 같이 같은 것을 볼 수 있습니다.
In [59]: print('B[1, 0, 2]=', B[1, 0, 2])
....: print('A[2, 1, 0]=', A[2, 1, 0])
....:
B[1, 0, 2]= 11
A[2, 1, 0]= 11
패딩¶
np.pad 함수를 이용하여 배열에 패딩을 더하는 작업을 할 수 있습니다.
np.pad(x, pad_width, mode) 형식으로 구성됩니다. x는 패딩될 배열이고 pad_width는 배열 x의 각 축별로 앞, 뒤로 패딩한 크기를 지정합니다.
1차원 배열
예를 들면 x가 1차원 배열이라면 pad_width=(1, 2)와 같이 하면 왼쪽은 1 칸, 오른쪽은 2 칸의 패딩을 하게 됩니다. mode는 패딩의 형식을 지정하는 것으로 'constant'일 때는 같은 값으로 채우게 됩니다. constant_values=(-1, -2)를 지정해서 왼쪽에는 -1, 오른쪽에는 -2 값을 채우도록 설정할 수 있습니다. pad_width가 정수 거나 (정수,) 형식이면 모든 축이 똑같은 정수 개만큼 패딩을 합니다.
In [60]: np.pad([1, 2, 3], (1, 2), 'constant', constant_values=(-1, -2))
....:
Out[60]: array([-1, 1, 2, 3, -2, -2])
pad_width=3으로 설정하면 왼쪽, 오른쪽 모두 3칸으로 패딩을 설정합니다. constant_values를 생략하면 기본값으로 0이 설정됩니다.
In [61]: np.pad([1, 2, 3], 3, 'constant')
....:
Out[61]: array([0, 0, 0, 1, 2, 3, 0, 0, 0])
2차원 배열
배열이 2차원일 때는 0축이 먼저 패딩되고 1축이 패딩되는 것을 볼 수 있습니다.
In [62]: x = np.arange(1, 13).reshape(3, 4)
....: x
....:
Out[62]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
모서리 값 설정에 주의해 보시기 바랍니다.
In [63]: np.pad(x, ((1, 2), (3, 4)), mode='constant', constant_values=((-1,-2), (-3, -4)))
....:
Out[63]:
array([[-3, -3, -3, -1, -1, -1, -1, -4, -4, -4, -4],
[-3, -3, -3, 1, 2, 3, 4, -4, -4, -4, -4],
[-3, -3, -3, 5, 6, 7, 8, -4, -4, -4, -4],
[-3, -3, -3, 9, 10, 11, 12, -4, -4, -4, -4],
[-3, -3, -3, -2, -2, -2, -2, -4, -4, -4, -4],
[-3, -3, -3, -2, -2, -2, -2, -4, -4, -4, -4]])
3차원 배열
3차원 배열의 패딩을 보겠습니다. 특히 3차원 패딩할 때 0축 패딩은 0축과 같은 크기의 값을 만들어 값을 설정하는 것을 볼 수 있습니다.
In [64]: y = np.arange(1, 13).reshape(2, 3, 2)
....: y
....:
Out[64]:
array([[[ 1, 2],
[ 3, 4],
[ 5, 6]],
[[ 7, 8],
[ 9, 10],
[11, 12]]])
다음에서 보듯이 0축의 시작 부분에 크기가 2x3 배열을 추가하여 -1을 채우는 것을 알 수 있습니다.
In [65]: np.pad(y, ((1,0), (0,0), (0,0)), mode='constant', constant_values=((-1,-2), (-3,-4), (-5,-6)))
....:
Out[65]:
array([[[-1, -1],
[-1, -1],
[-1, -1]],
[[ 1, 2],
[ 3, 4],
[ 5, 6]],
[[ 7, 8],
[ 9, 10],
[11, 12]]])
다음은 0축의 끝부분에 2x3 배열을 추가하여 -2를 채웁니다.
In [66]: np.pad(y, ((1,1), (0,0), (0,0)), mode='constant', constant_values=((-1,-2), (-3,-4), (-5,-6)))
....:
Out[66]:
array([[[-1, -1],
[-1, -1],
[-1, -1]],
[[ 1, 2],
[ 3, 4],
[ 5, 6]],
[[ 7, 8],
[ 9, 10],
[11, 12]],
[[-2, -2],
[-2, -2],
[-2, -2]]])
다음은 0축에서 만들어진 패딩 배열에 1축의 모든 시작 부분에 (2,) 배열을 추가하여 -3을 채웁니다.
In [67]: np.pad(y, ((1,1), (1,0), (0,0)), mode='constant', constant_values=((-1,-2), (-3,-4), (-5,-6)))
....:
Out[67]:
array([[[-3, -3],
[-1, -1],
[-1, -1],
[-1, -1]],
[[-3, -3],
[ 1, 2],
[ 3, 4],
[ 5, 6]],
[[-3, -3],
[ 7, 8],
[ 9, 10],
[11, 12]],
[[-3, -3],
[-2, -2],
[-2, -2],
[-2, -2]]])
마찬가지로 0축에서 패딩된 배열에 1축의 모든 끝 부분에 (2,) 배열을 추가하여 -4을 채웁니다.
In [68]: np.pad(y, ((1,1), (1,1), (0,0)), mode='constant', constant_values=((-1,-2), (-3,-4), (-5,-6)))
....:
Out[68]:
array([[[-3, -3],
[-1, -1],
[-1, -1],
[-1, -1],
[-4, -4]],
[[-3, -3],
[ 1, 2],
[ 3, 4],
[ 5, 6],
[-4, -4]],
[[-3, -3],
[ 7, 8],
[ 9, 10],
[11, 12],
[-4, -4]],
[[-3, -3],
[-2, -2],
[-2, -2],
[-2, -2],
[-4, -4]]])
다음은 0, 1 축에서 패딩된 배열에 2 축의 시작부분에 -5를 채웁니다.
In [69]: np.pad(y, ((1,1), (1,1), (1,0)), mode='constant', constant_values=((-1,-2), (-3,-4), (-5,-6)))
....:
Out[69]:
array([[[-5, -3, -3],
[-5, -1, -1],
[-5, -1, -1],
[-5, -1, -1],
[-5, -4, -4]],
[[-5, -3, -3],
[-5, 1, 2],
[-5, 3, 4],
[-5, 5, 6],
[-5, -4, -4]],
[[-5, -3, -3],
[-5, 7, 8],
[-5, 9, 10],
[-5, 11, 12],
[-5, -4, -4]],
[[-5, -3, -3],
[-5, -2, -2],
[-5, -2, -2],
[-5, -2, -2],
[-5, -4, -4]]])
다음은 0, 1 축에서 패딩된 배열에 2 축의 끝부분에 -6를 채웁니다.
In [70]: np.pad(y, ((1,1), (1,1), (1,1)), mode='constant', constant_values=((-1,-2), (-3,-4), (-5,-6)))
....:
Out[70]:
array([[[-5, -3, -3, -6],
[-5, -1, -1, -6],
[-5, -1, -1, -6],
[-5, -1, -1, -6],
[-5, -4, -4, -6]],
[[-5, -3, -3, -6],
[-5, 1, 2, -6],
[-5, 3, 4, -6],
[-5, 5, 6, -6],
[-5, -4, -4, -6]],
[[-5, -3, -3, -6],
[-5, 7, 8, -6],
[-5, 9, 10, -6],
[-5, 11, 12, -6],
[-5, -4, -4, -6]],
[[-5, -3, -3, -6],
[-5, -2, -2, -6],
[-5, -2, -2, -6],
[-5, -2, -2, -6],
[-5, -4, -4, -6]]])
4차원 배열
In [71]: N = 2
....: C = 3
....: H = 4
....: W = 5
....: z = np.arange(N * C * H * W).reshape(N, C, H, W)
....: z
....:
Out[71]:
array([[[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[ 10, 11, 12, 13, 14],
[ 15, 16, 17, 18, 19]],
[[ 20, 21, 22, 23, 24],
[ 25, 26, 27, 28, 29],
[ 30, 31, 32, 33, 34],
[ 35, 36, 37, 38, 39]],
[[ 40, 41, 42, 43, 44],
[ 45, 46, 47, 48, 49],
[ 50, 51, 52, 53, 54],
[ 55, 56, 57, 58, 59]]],
[[[ 60, 61, 62, 63, 64],
[ 65, 66, 67, 68, 69],
[ 70, 71, 72, 73, 74],
[ 75, 76, 77, 78, 79]],
[[ 80, 81, 82, 83, 84],
[ 85, 86, 87, 88, 89],
[ 90, 91, 92, 93, 94],
[ 95, 96, 97, 98, 99]],
[[100, 101, 102, 103, 104],
[105, 106, 107, 108, 109],
[110, 111, 112, 113, 114],
[115, 116, 117, 118, 119]]]])
In [72]: np.pad(z, ((0,0), (0,0), (1,1), (2,2)), 'constant', constant_values=((-1,-2), (-3,-4), (-5,-6), (-7,-8)))
....:
Out[72]:
array([[[[ -7, -7, -5, -5, -5, -5, -5, -8, -8],
[ -7, -7, 0, 1, 2, 3, 4, -8, -8],
[ -7, -7, 5, 6, 7, 8, 9, -8, -8],
[ -7, -7, 10, 11, 12, 13, 14, -8, -8],
[ -7, -7, 15, 16, 17, 18, 19, -8, -8],
[ -7, -7, -6, -6, -6, -6, -6, -8, -8]],
[[ -7, -7, -5, -5, -5, -5, -5, -8, -8],
[ -7, -7, 20, 21, 22, 23, 24, -8, -8],
[ -7, -7, 25, 26, 27, 28, 29, -8, -8],
[ -7, -7, 30, 31, 32, 33, 34, -8, -8],
[ -7, -7, 35, 36, 37, 38, 39, -8, -8],
[ -7, -7, -6, -6, -6, -6, -6, -8, -8]],
[[ -7, -7, -5, -5, -5, -5, -5, -8, -8],
[ -7, -7, 40, 41, 42, 43, 44, -8, -8],
[ -7, -7, 45, 46, 47, 48, 49, -8, -8],
[ -7, -7, 50, 51, 52, 53, 54, -8, -8],
[ -7, -7, 55, 56, 57, 58, 59, -8, -8],
[ -7, -7, -6, -6, -6, -6, -6, -8, -8]]],
[[[ -7, -7, -5, -5, -5, -5, -5, -8, -8],
[ -7, -7, 60, 61, 62, 63, 64, -8, -8],
[ -7, -7, 65, 66, 67, 68, 69, -8, -8],
[ -7, -7, 70, 71, 72, 73, 74, -8, -8],
[ -7, -7, 75, 76, 77, 78, 79, -8, -8],
[ -7, -7, -6, -6, -6, -6, -6, -8, -8]],
[[ -7, -7, -5, -5, -5, -5, -5, -8, -8],
[ -7, -7, 80, 81, 82, 83, 84, -8, -8],
[ -7, -7, 85, 86, 87, 88, 89, -8, -8],
[ -7, -7, 90, 91, 92, 93, 94, -8, -8],
[ -7, -7, 95, 96, 97, 98, 99, -8, -8],
[ -7, -7, -6, -6, -6, -6, -6, -8, -8]],
[[ -7, -7, -5, -5, -5, -5, -5, -8, -8],
[ -7, -7, 100, 101, 102, 103, 104, -8, -8],
[ -7, -7, 105, 106, 107, 108, 109, -8, -8],
[ -7, -7, 110, 111, 112, 113, 114, -8, -8],
[ -7, -7, 115, 116, 117, 118, 119, -8, -8],
[ -7, -7, -6, -6, -6, -6, -6, -8, -8]]]])
matplotlib¶
딥러닝 실험에서는 그래프 그리기와 데이터 시각화도 중요합니다. matplotlib은 그래프를 그려주는 라이브러리입니다. matplotlib을 사용하면 그래프 그리기와 데이터 시각화가 쉬워집니다. 이번 절에서는 그래프를 그리고 이미지를 화면에 표시하는 방법을 설명합니다.
단순한 그래프 그리기¶
그래프를 그리려면 matplotlib의 pyplot 모듈을 이용합니다. sin 함수를 그리는 예를 살펴봅니다.
import numpy as np
import matplotlib.pyplot as plt
# 데이터 준비
x = np.arange(0, 6, 0.1) # 0에서 6까지 0.1 간격으로 생성
y = np.sin(x)
# 그래프 그리기
plt.plot(x, y)
plt.show()
이 코드에서는 넘파이의 arange 메서드로 [0, 0.1, 0.2, …, 5.8, 5.9]라는 데이터를 생성하여 변수 x에 할당했습니다. 그다음 줄에서는 x의 각 원소에 넘파이의 sin 함수인 np.sin( )을 적용하여 변수 y에 할당합니다. 이제 x와 y를 인수로 plt.plot 메서드를 호출해 그래프를 그립니다. 마지막으로 plt.show( )를 호출해 그래프를 화면에 출력하고 끝납니다. 이 코드를 실행하면 [그림 1-3]의 이미지가 그려집니다.
(Source code, png, hires.png, pdf)
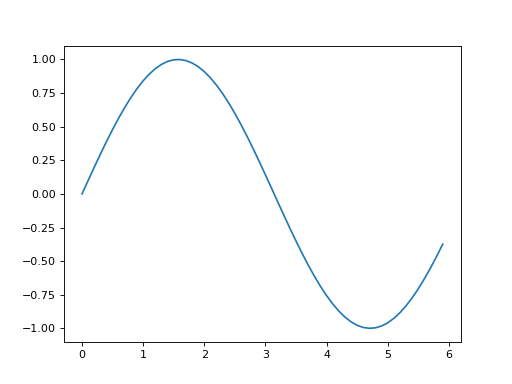
그림 1-3 sin 함수 그래프
pyplot의 기능¶
여기에 cos 함수도 추가로 그려보겠습니다. 또, 제목과 각 축의 이름(레이블) 표시 등, pyplot의 다른 기능도 사용해보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
# 데이터 준비
x = np.arange(0, 6, 0.1) # 0에서 6까지 0.1 간격으로 생성
y1 = np.sin(x)
y2 = np.cos(x)
# 그래프 그리기
plt.plot(x, y1, label="sin")
plt.plot(x, y2, linestyle = "--", label="cos") # cos 함수는 점선으로 그리기
plt.xlabel("x") # x축 이름
plt.ylabel("y") # y축 이름
plt.title('sin & cos') # 제목
plt.legend() # 범례: 기본은 label 값 출력
plt.show()
결과는 [그림 1-4]와 같습니다. 그래프의 제목과 축 이름이 보일 겁니다.
(Source code, png, hires.png, pdf)
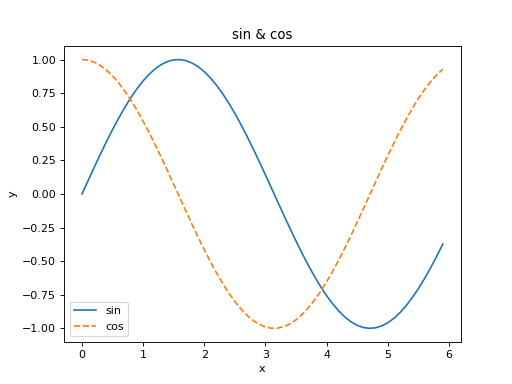
그림 1-4 sin 함수와 cos 함수 그래프
한글 폰트¶
폰트는 font_manager를 이용합니다.
시스템 폰트를 찾는 방법은 matplotlib.font_manager를 이용합니다.
In [73]: from matplotlib import font_manager
....:
....: fonts = font_manager.findSystemFonts()
....: fonts[:5] # 상위 5개를 출력합니다.
....:
Out[73]:
['C:\\Windows\\Fonts\\calibri.ttf',
'C:\\Windows\\Fonts\\timesbd.ttf',
'C:\\WINDOWS\\Fonts\\LG_Smart_UI-SemiBold.ttf',
'C:\\Windows\\Fonts\\LTYPEB.TTF',
'C:\\WINDOWS\\Fonts\\ariblk.ttf']
malgun 폰트가 있는지 확인해 봅니다.
In [74]: [font for font in fonts if 'malgun' in font]
....:
Out[74]:
['C:\\Windows\\Fonts\\malgunsl.ttf',
'C:\\Windows\\Fonts\\malgun.ttf',
'C:\\Windows\\Fonts\\malgunbd.ttf',
'C:\\WINDOWS\\Fonts\\malgun.ttf',
'C:\\WINDOWS\\Fonts\\malgunbd.ttf',
'C:\\WINDOWS\\Fonts\\malgunsl.ttf']
폰트를 설정합니다. rc는 리소스 설정을 하는 함수입니다.
import matplotlib.pyplot as plt
from matplotlib import font_manager
from matplotlib import rc
font_name = font_manager.FontProperties(fname='C:\\Windows\\Fonts\\malgun.ttf').get_name()
rc('font', family=font_name)
fig, ax = plt.subplots()
ax.plot([1, 2, 3], [3, 2, 1], label='한글 테스트')
ax.legend()
한글이 출력되는 것을 확인할 수 있습니다.
(Source code, png, hires.png, pdf)
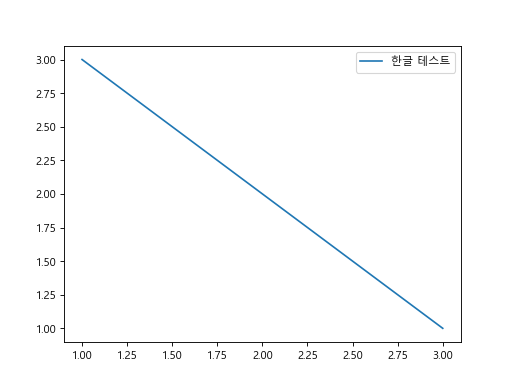
이미지 표시하기¶
pyplot에는 이미지를 표시해주는 메서드인 imshow()도 준비되어 있습니다. 이미지를 읽어들일 때는 matplotlib.image 모듈의 imread() 메서드를 이용합니다. 예를 보시죠.
import matplotlib.pyplot as plt
from matplotlib.image import imread
img = imread('apple.png') # 이미지 읽어오기(적절한 경로를 설정하세요!)
plt.imshow(img)
plt.show()
이 코드를 실행하면 [그림 1-5]처럼 읽어들인 이미지가 표시됩니다.
(Source code, png, hires.png, pdf)
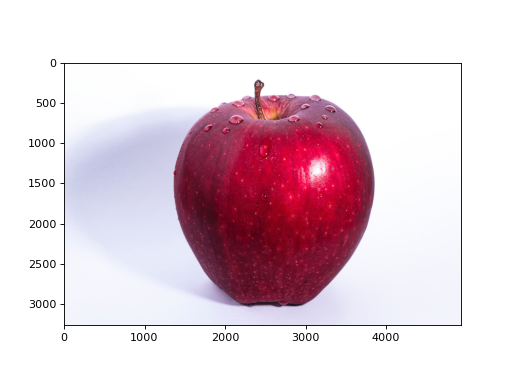
그림 1-5 이미지 표시하기
앞의 코드에서는 apple.png라는 이미지 파일이 현재 작업 디렉터리에 있다고 가정했습니다. 여러분은 자신의 환경에 맞게 파일 이름과 경로를 적절히 수정해야 합니다.
연습문제¶
다음 행렬 연산을 파이썬 넘파이 프로그램을 이용해서 계산하세요.
\[\begin{split}A = \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right], \quad B = \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{array}\right]\end{split}\]\(2A\)
A의 각 성분의 제곱\[\begin{split}\left[\begin{array}{ccc} 1^2 & 2^2 & 3^2 \\ 4^2 & 5^2 & 6^2 \end{array}\right]\end{split}\]두 행렬의 곱 \(AB\)
넘파이
reshape함수를 이용하여 다음과 같은 행렬을 만드세요.1 2 3 4 5 6 7 8 9 10 11 12
넘파이
zeros,ones,eye함수를 이용해3x5영행렬, 성분이 모두1로만 이루어진2x3행렬,5x5단위행렬을 각각 만드세요.넘파이
1x2와2x2배열을 더할 때 브로드캐스트 되는 과정을 자세히 설명하세요.다음 행렬
A의 원소가 0보다 작은 값을 모두 0으로 대체하세요.\[\begin{split}A = \left[\begin{array}{ccc} -1 & 2 & -5.4 \\ 0 & 1 & -100.5 \end{array}\right]\end{split}\]직사각형 클래스
Rectangle을 작성하는데,area(),diagonal()메소드를 갖도록 하세요.area는 직사각형의 면적을 출력하고diagonal은 직사각형의 대각선의 길이를 출력하는 프로그램을 작성하세요. 직사각형을 초기화할 때, 너비와 높이를 입력하도록__init__(self, width, height)메소드를 작성하세요.Dog클래스를 작성하는데 메소드는eat(),walk(),info()를 갖도록 하세요.eat메소드는 음식을 인자로 받아들이고,walk메소드를 실행할 때 마다 2미터씩 움직이도록 합니다.info()를 실행하면 이름이 뭐고, 무엇을 먹었고 얼마나 움직였는지를 출력하도록 프로그래밍을 하세요. 초기화할 때 강아지 이름을 입력할 수 있도록__init__(self, name)메소드를 작성하도록 하세요.