신경망

여기서 좀 더 복잡한 형태의 다층 퍼셉트론에 대해서 알아봅니다. 다층 퍼셉트론을 신경망이라고도 부릅니다. 신경망 학습은 다음 장에서 다룹니다.

용어

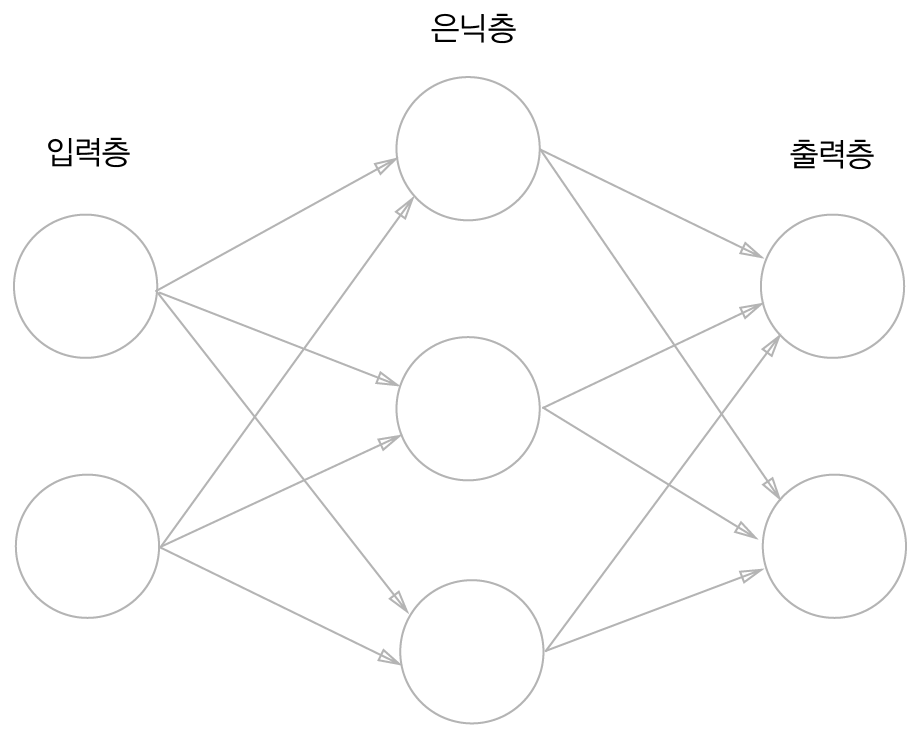
신경망을 아래 그림처럼 표시할 수 있습니다. 가장 왼쪽을 입력층(input layer), 맨 오른쪽을 출력층(output layer), 중간에 있는 것을 은닉층(hidden layer)이라 합니다. 입력층을 제외하고 나머지 층의 갯수로 신경망의 층수를 정의합니다. 따라서 그림은 2층 신경망이라고 합니다.

_images/nn_example.png

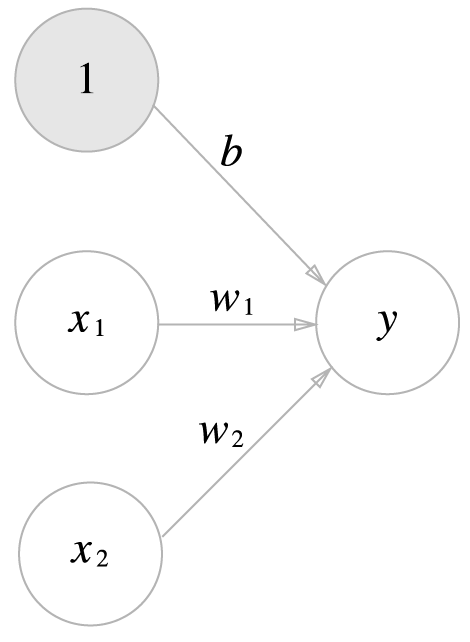
퍼셉트론을 식으로 다시 나타내면 다음과 같습니다.

\[\begin{split}y = \begin{cases} 0, & \text{if} \quad w_1 x_1 + w_2 x_2 + b <= 0 \\ 1, & \text{if} \quad w_1 x_1 + w_2 x_2 + b > 0 \end{cases}\end{split}\]

\(b\)는 편향 \(w_1\), \(w_2\)는 가중치라고 합니다. 편향을 포함하여 그림에 나타내면 다음과 같습니다.

_images/nn_bias.png

편향을 입력층과 같이 놓고 가중치를 b라고 하면 다음과 같이 쉽게 퍼셉트론을 표현할 수 있습니다.

\[\begin{split}\mathbf{x} = (1, x_1, x_2) \\ \mathbf{w} = (b, w_1, w_2) \\ a = \mathbf{w} \cdot \mathbf{x} \\ y = h(a) \\ h(a) = \begin{cases} 0, & \text{if} \quad a <= 0 \\ 1, & \text{if} \quad a > 0 \end{cases}\end{split}\]

여기서 \(h(x)\)를 활성화함수(activation function)라고 합니다. 활성화함수는 입력 신호의 총합이 활성화를 일으키는지(1) 아닌지(0)를 정하는 역할을 합니다.

활성화 함수의 처리과정을 담은 그림은 다음과 같습니다.

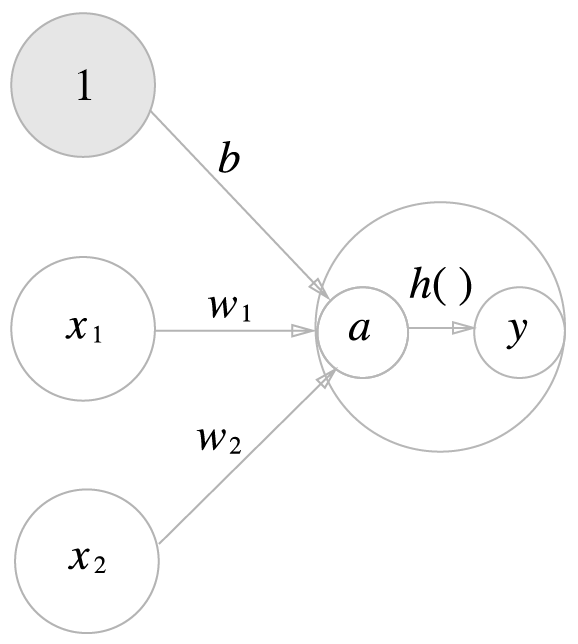
_images/nn_activation.png

그림에서 원을 노드 또는 뉴런이라고 부릅니다.

활성화 함수

이제까지는 활성화 함수로 계단함수(step function)을 사용했습니다. 계단함수 외에도 신경망에서 자주 사용되는 활성화함수에 대해서 알아봅니다.

계단함수

계단함수를 다음과 같이 파이썬을 이용해 정의할 수 있습니다.

In [1]: def step_function(x):
   ...:   if x > 0:
   ...:     return 1
   ...:   else:
   ...:     return 0
   ...:

하지만 x가 벡터로 입력되면 x > 0 부분에 문제가 생기는 것을 알 수 있습니다. 이런 것을 피하기 위해 넘파이 배열과 astype 함수를 이용하면 간단하게 작성할 수 있습니다.

In [2]: def step_function(x):
   ...:   y = x > 0
   ...:   return y.astype(np.int)
   ...:

x가 넘파이 배열이면 비교를 통해 True, False로 이루어진 배열로 변경되는 것을 알 수 있습니다.

In [3]: import numpy as np
   ...: x = np.array([-1.0, 0.0, 1.0])
   ...: y = x > 0
   ...: y
   ...: 
Out[3]: array([False, False,  True])

따라서 y는 논리형 배열인 것을 확인할 수 있습니다. y.astype(np.int)는 넘파이 배열 y를 정수형으로 변환을 합니다. 정수형으로 변환할 때 True는 1로, False는 0으로 변경됩니다.

In [4]: y.astype(np.int)
Out[4]: array([0, 0, 1])

계단함수의 그래프는 다음과 같습니다.

import numpy as np
import matplotlib.pyplot as plt

def step_function(x):
  return np.array(x > 0, dtype=np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.grid()
plt.ylim(-0.1, 1.1)
plt.show()

(Source code, png, hires.png, pdf)

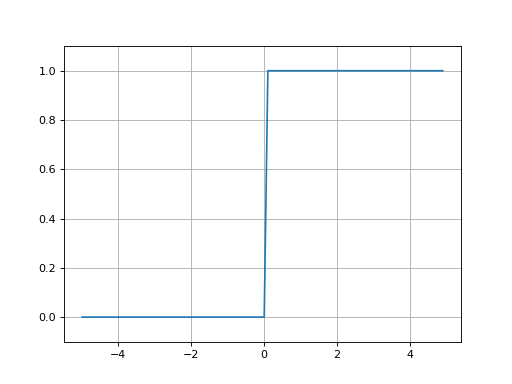
_images/NeuralNetworks-1.png

시그모이드 함수

시그모이드 함수는 0과 1 사이의 값을 부드러운 S자 곡선을 갖는 함수입니다.

\[h(x) = \frac{1}{1 + e^{-x}}\]

시그모이드함수를 넘파이를 이용하여 구현합니다.

In [5]: def sigmoid(x):
   ...:   return 1 / (1 + np.exp(-x))
   ...:

넘파이 배열이 입력되면 넘파이 배열이 출력됩니다.

In [6]: x = np.array([-1.0, 1.0, 2.0])
   ...: sigmoid(x)
   ...: 
Out[6]: array([0.26894142, 0.73105858, 0.88079708])

시그모이드함수를 그래프로 그립니다.

In [7]: x = np.arange(-5.0, 5.0, 0.1)
   ...: y = sigmoid(x)
   ...: plt.cla() # 이전 플롯 삭제
   ...: plt.plot(x, y);
   ...: plt.grid()
   ...: plt.ylim(-0.1, 1.1);
   ...:
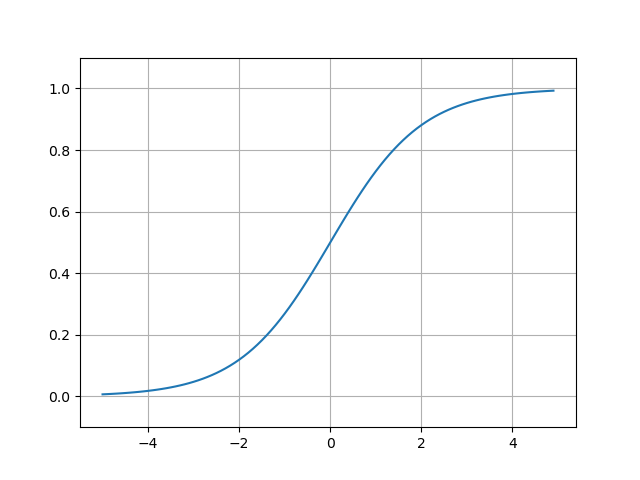
_images/plot_sigmoid.png

계단함수와 시그모이드함수를 함께 그립니다.

In [8]: x = np.arange(-5.0, 5.0, 0.1)
   ...: y1 = step_function(x)
   ...: y2 = sigmoid(x)
   ...: plt.cla()
   ...: plt.plot(x, y1, x, y2);
   ...: plt.grid()
   ...: plt.legend(['step', 'sigmoid']);
   ...:
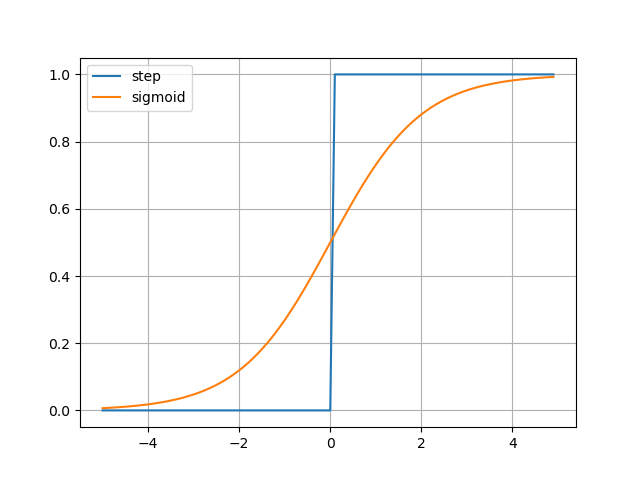
_images/plot_step_sigmoid.png

ReLU 함수

활성화함수로 최근에는 ReLU(rectified Linear Unit)함수를 많이 사용하고 있습니다. ReLU는 입력이 0보다 작거나 같으면 0을 출력하고 그렇지않으면 입력값을 그대로 출력하는 함수입니다.

\[\begin{split}h(x) = \begin{cases} x, & \text{if} \quad x > 0 \\ 0, & \text{if} \quad x <= 0 \\ \end{cases}\end{split}\]

넘파이를 이용하여 정의하면 다음과 같습니다.

In [9]: def relu(x):
   ...:   return np.maximum(0, x)
   ...:

np.maximum(x1, x2)는 x1, x2 중에서 가장 큰 원소를 반환합니다. 두 배열의 크기가 다르면 브로드캐스트를 하고 각 성분에서 가장 큰 원소를 반환합니다.

In [10]: import matplotlib.pyplot as plt
   ....: plt.cla()
   ....: x = np.linspace(-5.0, 5.0, 100)
   ....: y = relu(x)
   ....: plt.grid()
   ....: plt.plot(x, y);
   ....: plt.xlim(-6.0, 6.0);
   ....:
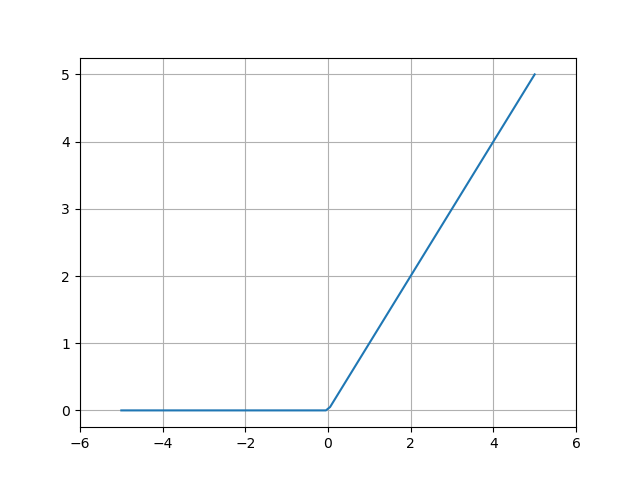
_images/plot_relu.png

np.linspace(start, stop, num) 함수는 start에서부터 stop까지 num 개의 숫자를 등간격으로 나눠 넘파이 배열로 반환합니다.

행렬 연산

행렬은 다음과 같이 표시합니다.

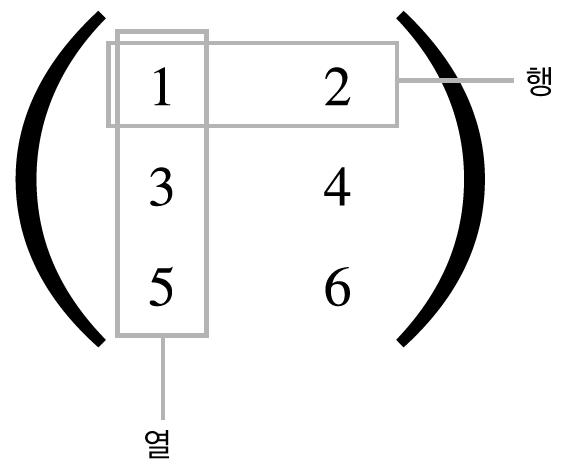
_images/matrix.png

행렬의 곱

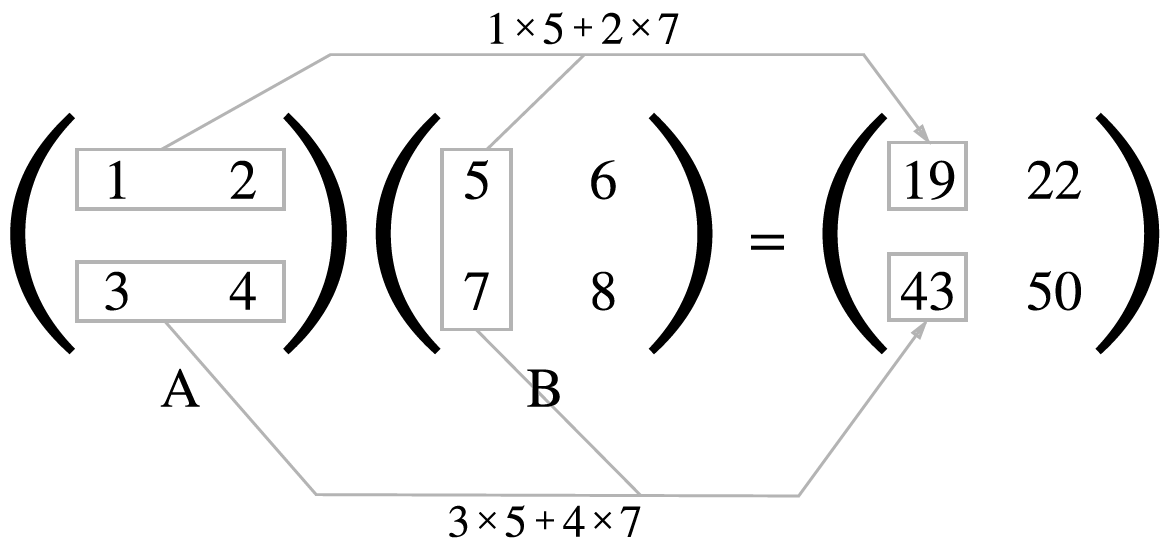
_images/matrix_mult.png

넘파이 계산을 하면 다음과 같습니다.

In [11]: A = np.arange(1, 5).reshape(2, 2)
   ....: print(A.shape)
   ....: B = np.arange(5, 9).reshape(2, 2)
   ....: np.dot(A, B)
   ....: 
(2, 2)
Out[11]: 
array([[19, 22],
       [43, 50]])

np.dot()를 이용하여 두 행렬의 곱을 할 수 있습니다.

행렬의 곱은 앞 행렬의 열의 수와 뒤 행렬의 행의 수가 같을 때문 연산이 가능합니다.

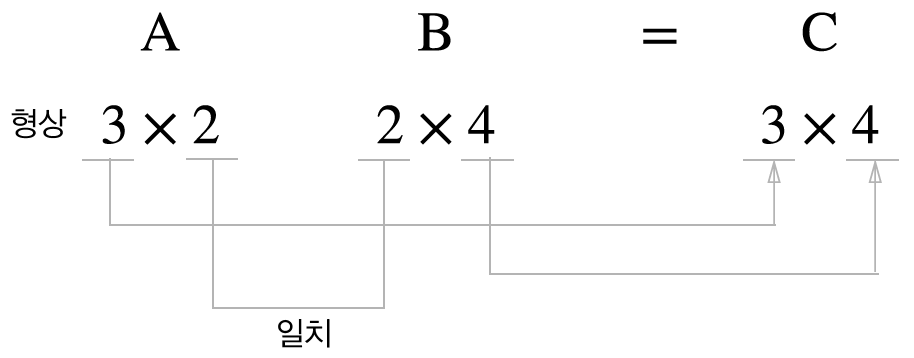
_images/mat_mult_op.png 
In [12]: A= np.arange(6).reshape(3, 2)
   ....: print(A.shape)
   ....: B = np.arange(8).reshape(2, 4)
   ....: print(B.shape)
   ....: A.dot(B)
   ....: 
(3, 2)
(2, 4)
Out[12]: 
array([[ 4,  5,  6,  7],
       [12, 17, 22, 27],
       [20, 29, 38, 47]])

신경망 계산

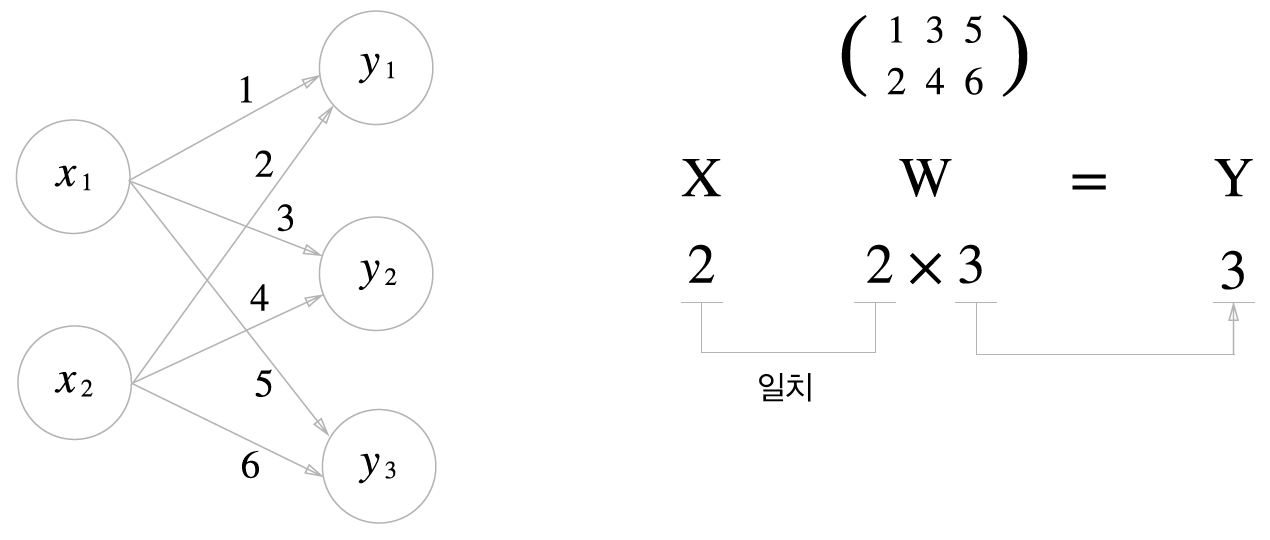
_images/nn_mult.png

\(\mathbf{X}\)는 입력값을 \(\mathbf{W}\)는 가중치, \(\mathbf{Y}\)는 출력값을 나타냅니다.

예를 들어 \(x_1 = 1\), \(x_2=2\)이고 가중치는 각각 \((1,2), (3, 4), (5, 6)\)이라고 하면 넘파이를 이용하여 다음과 같이 계산할 수 있습니다.

In [13]: X = np.array([1, 2])
   ....: W = np.array([[1, 3, 5], [2, 4, 6]])
   ....: print('W=', W)
   ....: Y = np.dot(X, W)
   ....: print('Y=', Y)
   ....: 
W= [[1 3 5]
 [2 4 6]]
Y= [ 5 11 17]

3층 신경망

좀더 복잡한 구조인 3층 신경망 구현을 알아봅니다.

앞으로 구현할 신경망은 다음과 같은 그림으로 구성된다고 가정합니다. 입력층과 2개의 은닉층 및 출력층으로 이루어져 있습니다.

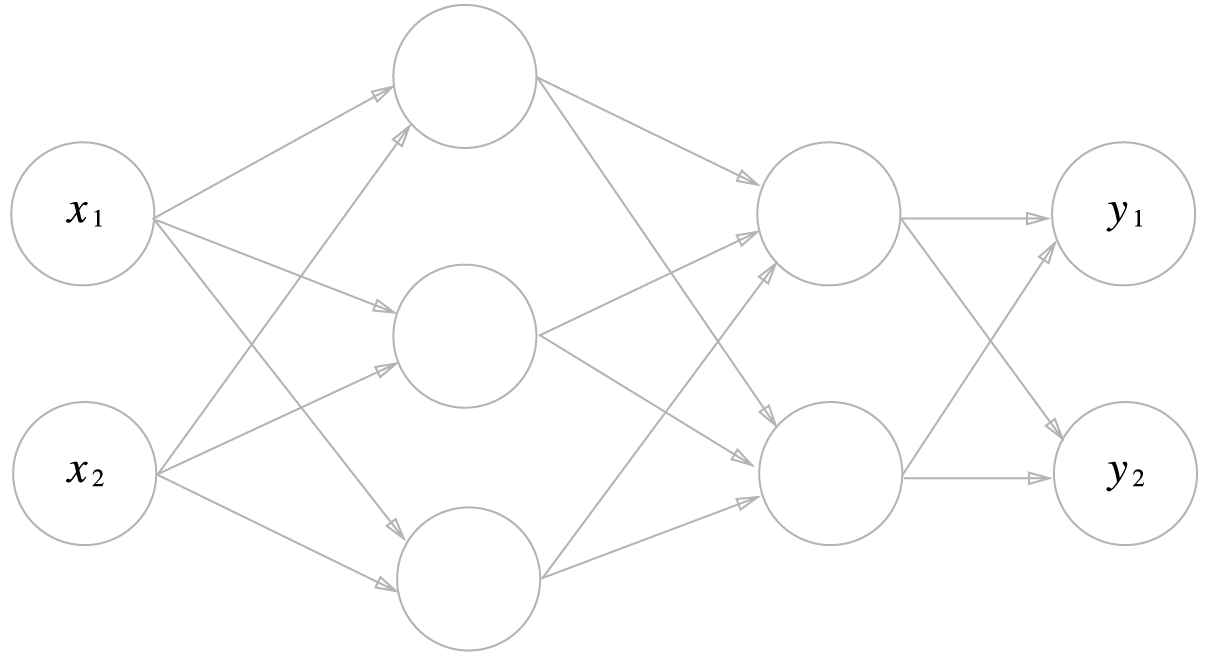
_images/nn_3layer.png

입력층은 2차원 자료 \((x_1, x_2)\)가 들어오고 첫번째 은닉층의 노드는 3개, 두번째 은닉층의 노드는 2개, 마지막 출력층의 노드는 2개로 구성됩니다.

표기법

계산의 편의를 위해 표기법을 정의합니다.

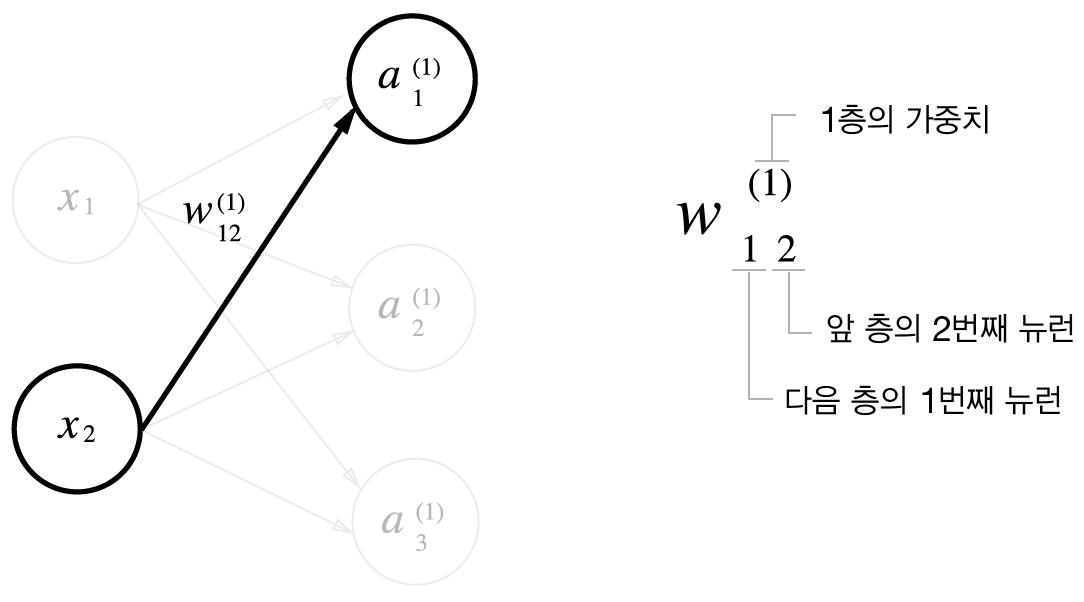
_images/nn_3layer_notation.png

오른쪽 위의 괄호는 층수를 나타내고 아래쪽에서 오른쪽 수는 앞층 노드의 인덱스를, 왼쪽 수는 다음 층 노드의 인덱스를 나타냅니다. \(a\)는 가중치와 입력값들의 곱의 합을 의미합니다.

편향을 추가한 그림입니다.

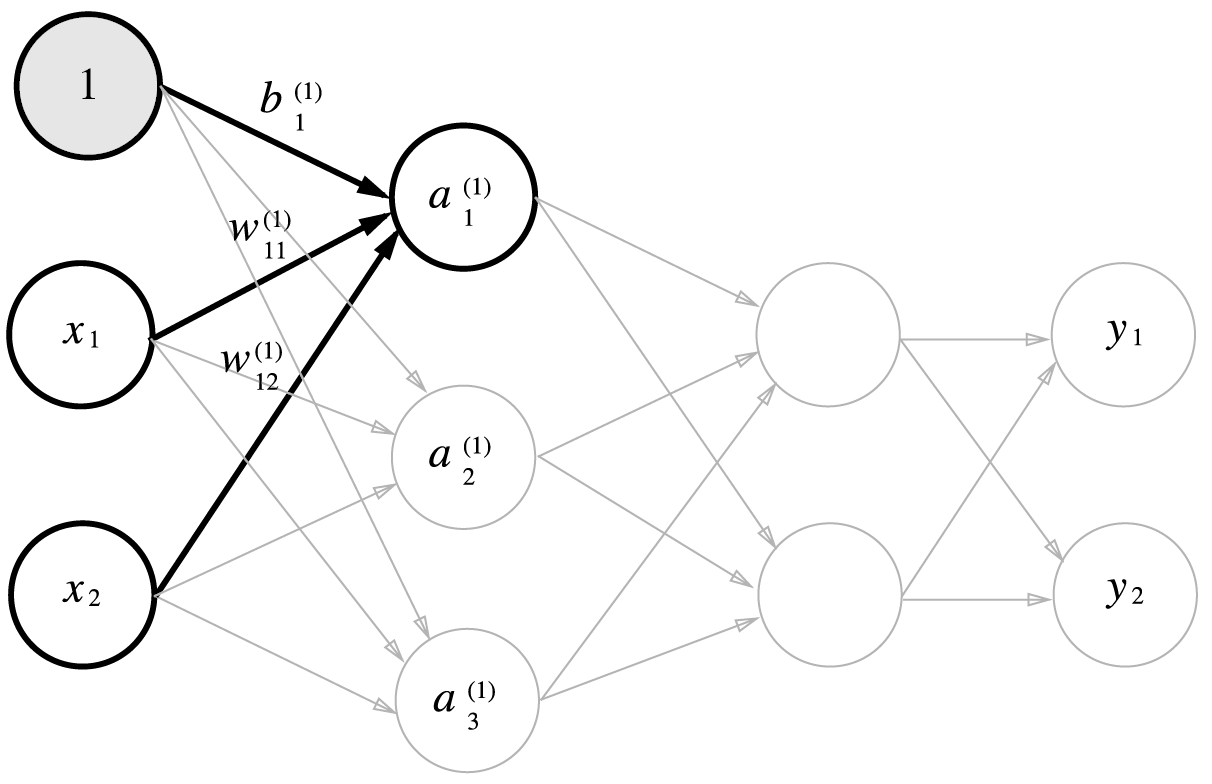
_images/nn_3layer_bias.png

첫번째 은닉층(1층)의 계산식은 다음과 같습니다.

\[\begin{split}a_1^{(1)} = w_{11}^{(1)} x_1 + w_{12}^{(1)} x_2 + b_1^{(1)} \\ a_2^{(1)} = w_{21}^{(1)} x_1 + w_{22}^{(1)} x_2 + b_2^{(1)} \\ a_3^{(1)} = w_{31}^{(1)} x_1 + w_{32}^{(1)} x_2 + b_3^{(1)}\end{split}\]

1층 은닉층 가중치 계산을 행렬로 표현하면 다음과 같습니다.

\[\mathbf{A}^{(1)} = \mathbf{X} \mathbf{W}^{(1)} + \mathbf{B}^{(1)}\]

여기서

\[\begin{split}\mathbf{X} = (x_1, x_2), \quad \mathbf{A}^{(1)} = (a_1^{(1)}, a_2^{(1)}, a_3^{(1)}), \quad \mathbf{B}^{(1)} = (b_1^{(1)}, b_2^{(1)}, b_3^{(1)}) \\ \mathbf{W}^{(1)} = \left(\begin{array}{ccc} w_{11}^{(1)} & w_{21}^{(1)} & w_{31}^{(1)} \\ w_{12}^{(1)} & w_{22}^{(1)} & w_{32}^{(1)} \\ \end{array}\right)\end{split}\]

입니다.

\[\begin{split}\mathbf{X} = (1.0, 0.5) \quad \mathbf{W}^{(1)} = \left(\begin{array}{ccc} 0.1 & 0.3 & 0.5 \\ 0.2 & 0.4 & 0.6 \\ \end{array}\right) \quad \mathbf{B}^{(1)} = (0.1, 0.2, 0.3)\end{split}\]

일 때, 넘파이를 이용해서 구현해봅니다.

In [14]: X = np.array([1.0, 0.5])
   ....: W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
   ....: B1 = np.array([0.1, 0.2, 0.3])
   ....: A1 = np.dot(X, W1) + B1
   ....: print(A1)
   ....: 
[0.3 0.7 1.1]

활성화함수 처리에 대한 그림을 그려봅니다.

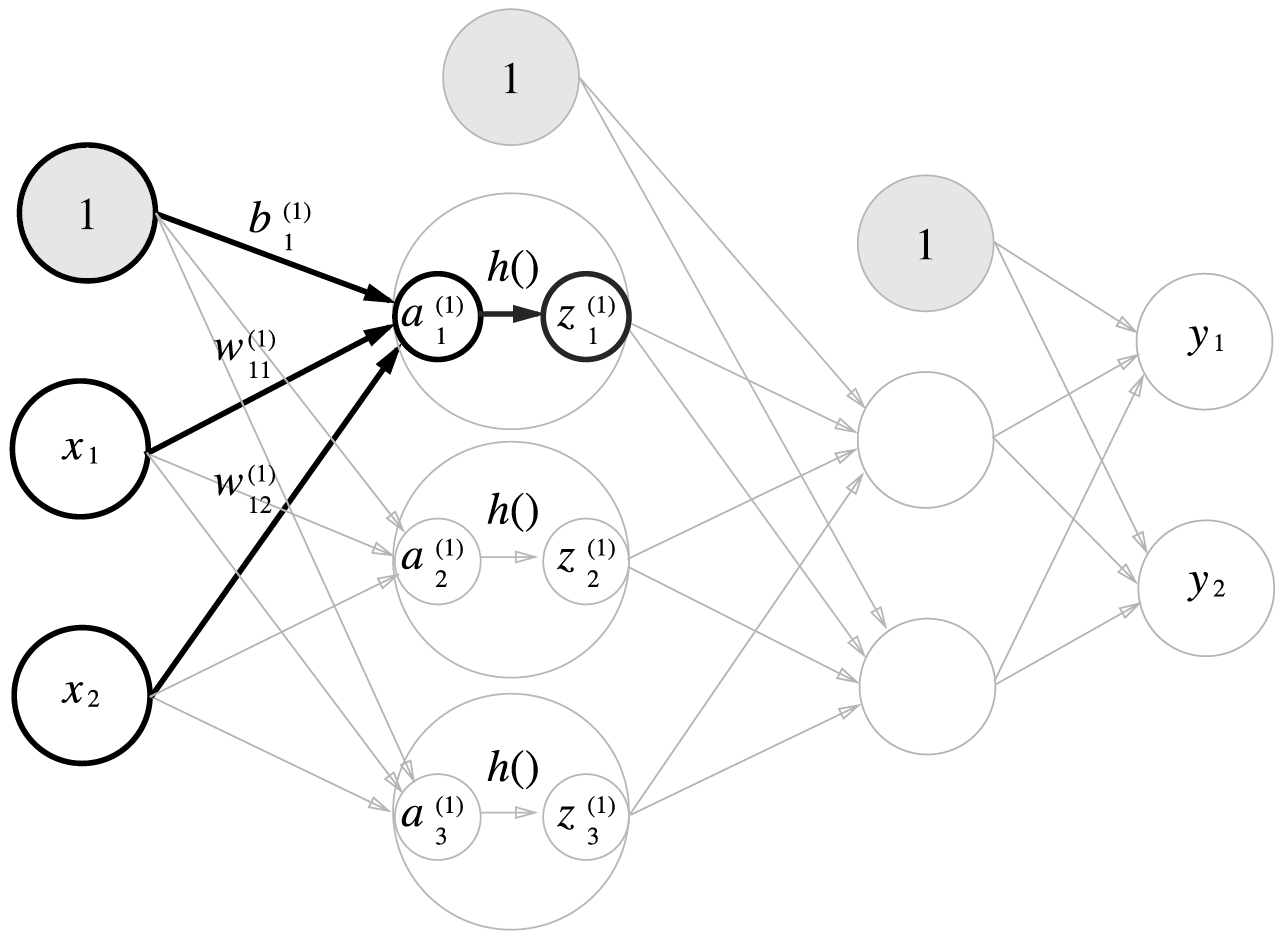
_images/nn_3layer_activation.png

활성화함수로 여기서는 시그모이드함수를 사용하겠습니다. 활성화함수를 거쳐서 나온 값을 \(z\)라고 표기하겠습니다.

\[\begin{split}\mathbf{Z}^{(1)} = \mathbf{h}(\mathbf{A}^{(1)}) \\\end{split}\]

여기서 활성화 벡터함수 \(\mathbf{h}: \mathbf{R}^n \to \mathbf{R}^n\)는 다음과 같이 정의합니다.

\[\begin{split}\mathbf{h}(\mathbf{x}) = (h(x_1), h(x_2), \ldots, h(x_j), \ldots, h(x_n)) \\ \mathbf{x} = (x_1, x_2, \ldots, x_n) \in \mathbf{R}^n\end{split}\]

여기서 \(h(x)\)는 적당한 활성화함수입니다. 예를 들어 시그모이드 활성화함수일 때

\[h(x_j) = \frac{1}{1 + e^{-x_j}}\]

가 됩니다. 앞에서 정의한 파이썬 시그모이드함수 sigmoid()를 이용하면 다음과 같이 구할 수 있습니다.

In [15]: Z1 = sigmoid(A1)
   ....: print('A1=', A1)
   ....: print('Z1=', Z1)
   ....: 
A1= [0.3 0.7 1.1]
Z1= [0.57444252 0.66818777 0.75026011]

다음으로 1층에서 2층으로 가는 과정을 살펴봅니다.

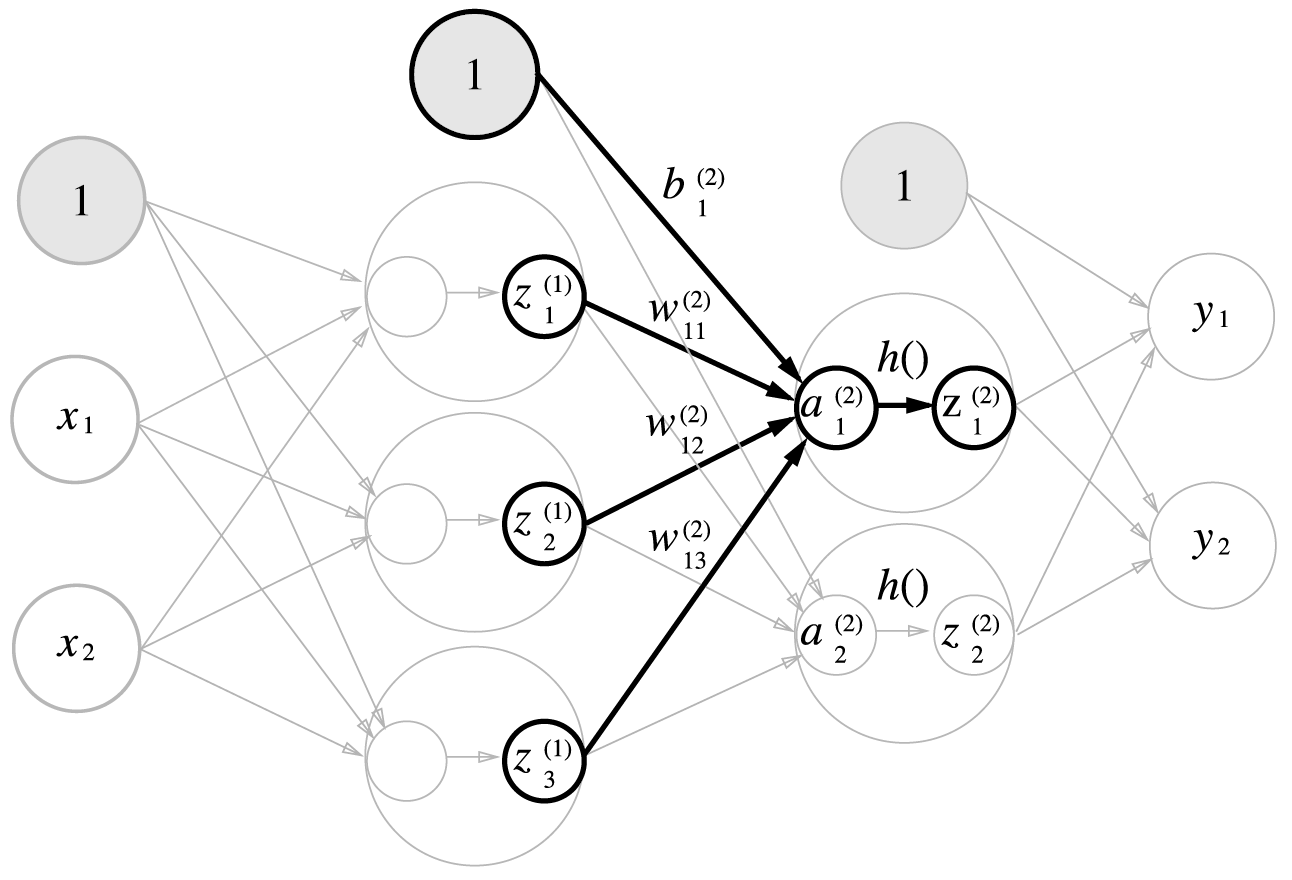
_images/nn_3layer_2nd.png

2층 은닉층 가중치 계산을 행렬로 표현하면 다음과 같습니다.

\[\mathbf{A}^{(2)} = \mathbf{Z}^{(1)} \mathbf{W}^{(2)} + \mathbf{B}^{(2)}\]

여기서

\[\begin{split}\mathbf{Z}^{(1)} = (z_1^{(1)}, z_2^{(1)}, z_3^{(1)}), \quad \mathbf{W}^{(2)} = \left(\begin{array}{cc} w_{11}^{(2)} & w_{21}^{(2)} \\ w_{12}^{(2)} & w_{22}^{(2)} \\ w_{13}^{(2)} & w_{23}^{(2)} \\ \end{array}\right) , \quad \mathbf{B}^{(2)} = (b_1^{(2)}, b_2^{(2)}), \quad \mathbf{A}^{(2)} = (a_1^{(2)}, a_2^{(2)})\end{split}\]

입니다.

\[\begin{split}\mathbf{W}^{(2)} = \left(\begin{array}{ccc} 0.1 & 0.4 \\ 0.2 & 0.5 \\ 0.3 & 0.6 \\ \end{array}\right) \quad \mathbf{B}^{(2)} = (0.1, 0.2)\end{split}\]

일 때, 넘파이를 이용해서 구현해봅니다.

In [16]: W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
   ....: B2 = np.array([0.1, 0.2])
   ....: A2 = np.dot(Z1, W2) + B2
   ....: print(A1)
   ....: Z2 = sigmoid(A2)
   ....: print(Z2)
   ....: 
[0.3 0.7 1.1]
[0.62624937 0.7710107 ]

마지막으로, 2층에서 출력층으로 가는 계산과정입니다.

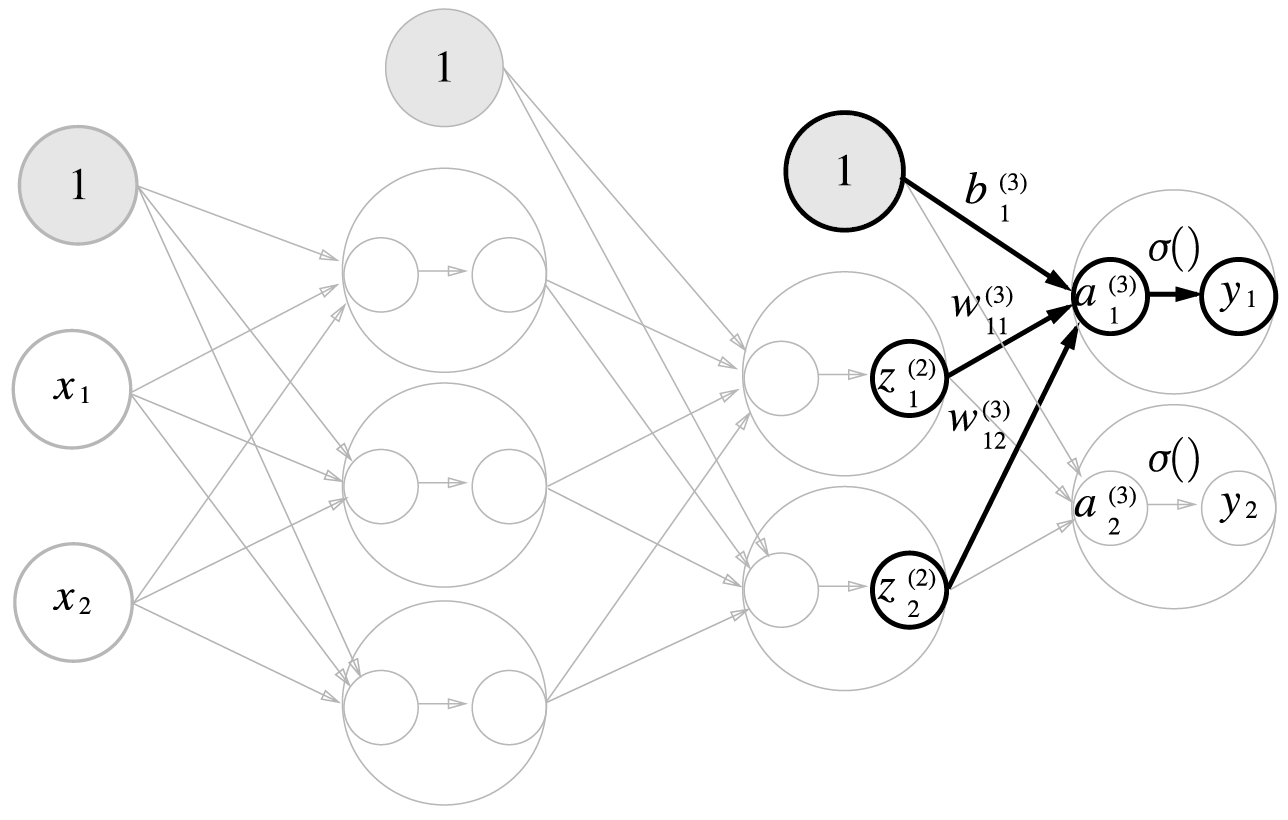
_images/nn_3layer_last.png

3층 출력층 가중치 계산을 행렬로 표현하면 다음과 같습니다.

\[\mathbf{A}^{(3)} = \mathbf{Z}^{(2)} \mathbf{W}^{(3)} + \mathbf{B}^{(3)}\]

여기서

\[\begin{split}\mathbf{Z}^{(2)} = (z_1^{(2)}, z_2^{(2)}), \quad \mathbf{W}^{(3)} = \left(\begin{array}{cc} w_{11}^{(3)} & w_{21}^{(3)} \\ w_{12}^{(3)} & w_{22}^{(3)} \\ \end{array}\right) , \quad \mathbf{B}^{(3)} = (b_1^{(3)}, b_2^{(3)}), \quad \mathbf{A}^{(3)} = (a_1^{(3)}, a_2^{(3)})\end{split}\]

입니다.

출력층 활성화함수를 은닉층 활성화함수 \(h()\)와 다르게 \(\sigma()\)로 표현했습니다. 여기서는 출력층 활성화함수 \(\sigma()\)를 항등함수로 설정했습니다.

\[\sigma(x) = x\]

넘파이로 구현하면 다음과 같습니다.

\[\begin{split}\mathbf{W}^{(3)} = \left(\begin{array}{ccc} 0.1 & 0.3 \\ 0.2 & 0.4 \\ \end{array}\right) \quad \mathbf{B}^{(3)} = (0.1, 0.2)\end{split}\]
In [17]: def identity_function(x):
   ....:   return x
   ....: 
   ....: W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
   ....: B3 = np.array([0.1, 0.2])
   ....: 
   ....: A3 = np.dot(Z2, W3) + B3
   ....: Y = identity_function(A3)
   ....:

Note

출력층 활성화 함수는 문제의 성질에 따라 다르게 설정합니다. 예를 들어 회귀에는 항등함수를, 두 그룹으로 분류하는 문제에는 시그모이드 함수를, 다중 클래스 분류에는 소프트맥스 함수를 사용합니다.

구현 정리

In [18]: def init_network():
   ....:   network = {}
   ....:   network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
   ....:   network['b1'] = np.array([0.1, 0.2, 0.3])
   ....:   network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
   ....:   network['b2'] = np.array([0.1, 0.2])
   ....:   network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
   ....:   network['b3'] = np.array([0.1, 0.2])
   ....:   return network
   ....: 
   ....: def forward(network, x):
   ....:   W1, W2, W3 = network['W1'], network['W2'], network['W3']
   ....:   b1, b2, b3 = network['b1'], network['b2'], network['b3']
   ....: 
   ....:   a1 = np.dot(x, W1) + b1
   ....:   z1 = sigmoid(a1)
   ....:   a2 = np.dot(z1, W2) + b2
   ....:   z2 = sigmoid(a2)
   ....:   a3 = np.dot(z2, W3) + b3
   ....:   y = identity_function(a3)
   ....:   return y
   ....: 
   ....: network = init_network()
   ....: x = np.array([1.0, 0.5])
   ....: y = forward(network, x)
   ....: print(y)
   ....: 
[0.31682708 0.69627909]

init_network() 함수에서는 가중치와 편향을 초기화하고 forward() 함수에서는 초기값과 입력값을 가지고 출력값으로 변환하는 과정을 구현한 것입니다.

출력층

신경망은 회귀와 분류에 사용될 수 있습니다. 일반적으로 회귀에는 항등함수를 분류에는 소프트맥스 softmax 함수를 사용합니다.

소프트맥스 함수

소프트맥스 함수 \(\sigma : \mathbf{R}^n \to \mathbf{R}^n\)는 벡터함수로 다음과 같이 정의합니다.

\[\begin{split}\mathbf{\sigma}(\mathbf{x}) = (\sigma(x_1), \sigma(x_2), \ldots, \sigma(x_j), \ldots, \sigma(x_n)) \\ \sigma(x_j) = \frac{e^{x_j}}{\sum_{i=1}^n e^{x_i}}\end{split}\]

여기서

\[y_k = \sigma(a_k)\]

이고 \(n\)은 출력층의 노드 수, \(y_k\)는 \(k\) 번째 출력, \(a_k\)는 입력값입니다.

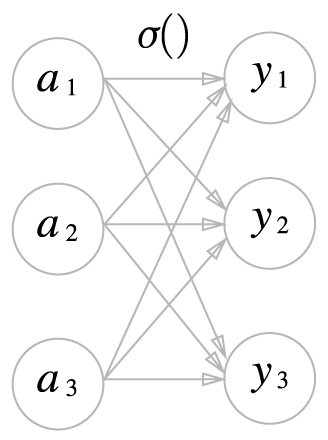
_images/nn_soft_out.png

간단하게 소프트맥스 함수를 넘파이로 다음과 같이 만들 수 있습니다.

In [19]: def softmax_naive(x):
   ....:   exp_x = np.exp(x)
   ....:   sum_exp_x = np.sum(exp_x)
   ....:   y = exp_x / sum_exp_x
   ....:   return y
   ....:

하지만 컴퓨터 계산할 때는 주의해야할 점이 있습니다. 컴퓨터로 숫자로 표현할 수 있는 한계가 있기 때문에 큰 숫자에 대해서는 오버플로(overflow) 오류를 발생시킬 수 있습니다. 가령 \(e^{1000}\)은 inf를 반환하기 때문에 잘못된 계산결과가 나올 수 있습니다. 이러한 문제를 해결하기 위해 소프트맥스 함수를 개선해봅니다.

\[\begin{split}\frac{e^{a_k}}{\sum_{i=1}^n e^{a_i}} &= \frac{C e^{a_k}}{C \sum_{i=1}^n e^{a_i}} \\ & = \frac{e^{(a_k + \log C)}}{\sum_{i=1}^n e^{(a_i + \log C)}} \\ & = \frac{e^{(a_k + C')}}{\sum_{i=1}^n e^{(a_i + C')}} \\\end{split}\]

위에서 영이 아닌 임의 수 \(C\)를 분모, 분자에 곱한 것은 지수에 임의의 수를 더한 것과 같습니다. 따라서 오버플로를 막기위해서 \(C'\)으로 입력값 중 가장 큰 값을 사용합니다.

In [20]: def softmax(x):
   ....:   if x.ndim == 2:
   ....:       x = x.T
   ....:       x = x - np.max(x, axis=0)
   ....:       y = np.exp(x) / np.sum(np.exp(x), axis=0)
   ....:       return y.T
   ....: 
   ....:   x = x - np.max(x) # 오버플로 방지
   ....:   return np.exp(x) / np.sum(np.exp(x))
   ....:

위에서 정의한 softmax 함수를 common 디렉토리의 functions.py 파일 안에 저장합니다.

출력층 노드수

출력층의 노드(뉴런)의 수는 문제에 맞게 설정해야합니다. 예를 들어 입력 이미지를 0부터 9로 분류하는 문제라면 출력층의 노드수는 분류할 이미지의 갯수와 같게 10으로 설정해야 합니다.

손글씨 숫자 인식

신경망의 구조를 응용할 수 있는 문제로 손글씨 분류를 다뤄봅니다. 여기서는 아직 학습 과정을 배우지 않았기때문에 신경망의 순전파 forward propagation에 대해서만 알아봅니다.

MNIST 데이터셋

MNIST Modified National Institute of Standards and Technology데이터셋은 기계학습 분야에서 자주 사용되는 손글씨 숫자 이미지를 모아 놓은 집합입니다. MNIST 데이터셋은 0부터 9까지 숫자 이미지로 구성되며 훈련 이미지 60,000장, 시험 이미지 10,000장으로 이루어져있습니다.

MNIST 이미지 데이터는 28x28 크기의 회색조 이미지이며 각 픽셀은 0부터 255까지의 값으로 이루어져있습니다. 각 이미지에는 그 이미지가 실제 의미하는 숫자 레이블이 함께 붙어 있습니다.

깃허브에서 다음 파일을 다운받아 현재 작업 디렉토리에 하위 디렉토리 dataset를 만들고 그 안에 mnist.py라고 저장합니다. 다음은 mnist.py 파일 내용입니다.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
# coding: utf-8
"""
from https://raw.githubusercontent.com/WegraLee/deep-learning-from-scratch/master/dataset/mnist.py
"""
try:
    import urllib.request
except ImportError:
    raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np


url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
    'train_img':'train-images-idx3-ubyte.gz',
    'train_label':'train-labels-idx1-ubyte.gz',
    'test_img':'t10k-images-idx3-ubyte.gz',
    'test_label':'t10k-labels-idx1-ubyte.gz'
}

dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"

train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784


def _download(file_name):
    file_path = dataset_dir + "/" + file_name
    
    if os.path.exists(file_path):
        return

    print("Downloading " + file_name + " ... ")
    urllib.request.urlretrieve(url_base + file_name, file_path)
    print("Done")
    
def download_mnist():
    for v in key_file.values():
       _download(v)
        
def _load_label(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
            labels = np.frombuffer(f.read(), np.uint8, offset=8)
    print("Done")
    
    return labels

def _load_img(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")    
    with gzip.open(file_path, 'rb') as f:
            data = np.frombuffer(f.read(), np.uint8, offset=16)
    data = data.reshape(-1, img_size)
    print("Done")
    
    return data
    
def _convert_numpy():
    dataset = {}
    dataset['train_img'] =  _load_img(key_file['train_img'])
    dataset['train_label'] = _load_label(key_file['train_label'])    
    dataset['test_img'] = _load_img(key_file['test_img'])
    dataset['test_label'] = _load_label(key_file['test_label'])
    
    return dataset

def init_mnist():
    download_mnist()
    dataset = _convert_numpy()
    print("Creating pickle file ...")
    with open(save_file, 'wb') as f:
        pickle.dump(dataset, f, -1)
    print("Done!")

def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))
    for idx, row in enumerate(T):
        row[X[idx]] = 1
        
    return T
    

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """MNIST 데이터셋 읽기
    
    Parameters
    ----------
    normalize : 이미지의 픽셀 값을 0.0~1.0 사이의 값으로 정규화할지 정한다.
    one_hot_label : 
        one_hot_label이 True면、레이블을 원-핫(one-hot) 배열로 돌려준다.
        one-hot 배열은 예를 들어 [0,0,1,0,0,0,0,0,0,0]처럼 한 원소만 1인 배열이다.
    flatten : 입력 이미지를 1차원 배열로 만들지를 정한다. 
    
    Returns
    -------
    (훈련 이미지, 훈련 레이블), (시험 이미지, 시험 레이블)
    """
    if not os.path.exists(save_file):
        init_mnist()
        
    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)
    
    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0
            
    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])    
    
    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) 


if __name__ == '__main__':
    init_mnist()

그리고 다음과 같이 실행하면 처음 한 번 실행될 때만 파일을 인터넷에서 다운받아 dataset 디렉토리에 저장하고 다음부터는 그 안에 있는 피클(pickle) 파일로부터 데이터셋을 로드합니다.

In [21]: import sys, os
   ....: sys.path.append(os.path.join(os.getcwd(), 'src'))
   ....: from dataset.mnist import load_mnist
   ....: (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
   ....: print(x_train.shape)
   ....: print(t_train.shape)
   ....: print(x_test.shape)
   ....: print(t_test.shape)
   ....: 
(60000, 784)
(60000,)
(10000, 784)
(10000,)

load_mnist 함수는 MNIST 데이터를 (훈련이미지, 훈련레이블), (시험이미지, 시험레이블) 형식으로 반환합니다. 인수로는 normalize, flatten, one_hot_label 3가지를 설정할수 있습니다. normalize는 입력이미지의 값을 0부터 1까지의 값으로 정규화할 지를 정합니다. flatten 인수는 입력이미지를 1차원 배열로 만들지를 정합니다. one_hot_label은 원핫인코딩(one-hot encoding) 형식으로 레이블을 반환할지를 정합니다.

원핫인코딩이란 레이블 중에서 정답에 해당하는 원소만 1이고 나머지는 0으로 설정한 것을 말합니다.

MNIST 이미지를 출력하도록 합니다.

In [22]: import sys, os
   ....: sys.path.append(os.pardir)
   ....: import numpy as np
   ....: from dataset.mnist import load_mnist
   ....: import matplotlib.pyplot as plt
   ....: 
   ....: (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
   ....: img = x_train[0]
   ....: label = t_train[0]
   ....: print(label)
   ....: 
   ....: print(img.shape)
   ....: img = img.reshape(28, 28)
   ....: print(img.shape)
   ....: plt.cla()
   ....: plt.imshow(img, cmap='Greys');
   ....:
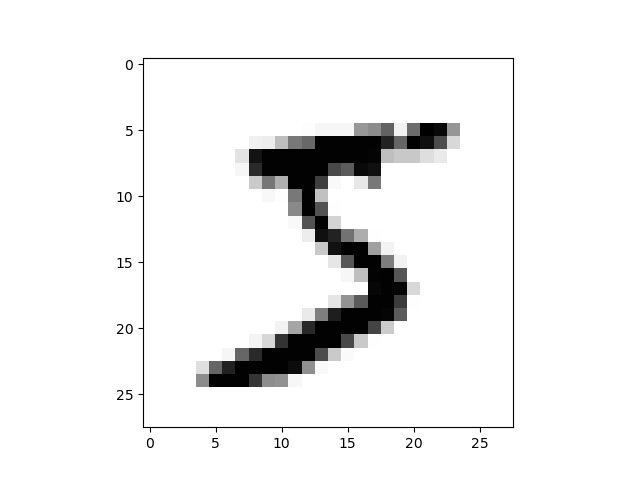
_images/plot_mnist_sample.png

MNIST 처리

여기서는 미리 만들어 둔 가중치 매개변수 파일 sample_weight.pkl을 이용해서 MNIST 테스트셋에 대한 추론을 구현해봅니다. 우선 이곳에서 sample_weight.pkl 파일을 다운받아 ch03 디렉토리에 저장합니다. 여기서 사용할 신경망은 입력층 노드가 784(28x28)개, 출력층 노드가 10개 입니다. 은닉층은 2개로 이루어지며 첫번째 은닉층의 노드 갯수는 50개, 두번째는 100개로 구성됩니다.

get_data() 함수를 이용해 MNIST 데이터셋 중에서 테스트 데이터셋만을 반환받습니다. 가중치 매개변수 데이터 sample_weight는 이미 훈련데이터를 이용해서 학습되었기 때문에 여기서는 필요하지 않습니다.

In [23]: def get_data():
   ....:   (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
   ....:   return x_test, t_test
   ....:

load_mnist 함수의 인자 중 normalize=True를 사용해서 이미지 값들을 0과 1사이의 값으로 정규화합니다.

init_network() 함수를 이용해 미리 학습해 둔 가중치 매개변수 데이터를 불러옵니다.

In [24]: def init_network():
   ....:   import pickle
   ....:   with open('sample_weight.pkl', 'rb') as f:
   ....:     network = pickle.load(f)
   ....:   return network
   ....:

이 데이터는 딕셔너리 형식이고 W1, W2, W3, b1, b2, b3 값들로 이루어져 있습니다.

In [25]: network = init_network()
   ....: type(network)
   ....: network.keys()
   ....: 
Out[25]: dict_keys(['b2', 'W1', 'b1', 'W2', 'W3', 'b3'])

딕셔너리 함수 keys()를 이용해 키들을 확인할 수 있습니다. items() 함수를 이용하면 딕셔너리의 키, 값 쌍을 반환받을 수 있습니다.

In [26]: for key, val in network.items():
   ....:   print('키: {}, 값의 크기: {}'.format(key, val.shape))
   ....: 
키: b2, 값의 크기: (100,)
키: W1, 값의 크기: (784, 50)
키: b1, 값의 크기: (50,)
키: W2, 값의 크기: (50, 100)
키: W3, 값의 크기: (100, 10)
키: b3, 값의 크기: (10,)

predict() 함수는 가중치와 숫자 이미지 입력값 하나를 입력받아 처리를 한 후 결과값으로 입력된 이미지에 대응되는 추정된 숫자에 대한 확률값 배열을 반환합니다. 이 부분이 신경망 추론 부분에 해당하고 여기서는 3층으로 이루어져 있습니다.

In [27]: def predict(network, x):
   ....:   W1, W2, W3 = network['W1'], network['W2'], network['W3']
   ....:   b1, b2, b3 = network['b1'], network['b2'], network['b3']
   ....: 
   ....:   a1 = np.dot(x, W1) + b1
   ....:   z1 = sigmoid(a1)
   ....:   a2 = np.dot(z1, W2) + b2
   ....:   z2 = sigmoid(a2)
   ....:   a3 = np.dot(z2, W3) + b3
   ....:   y = softmax(a3)
   ....:   return y
   ....:

다음으로 테스트 이미지 데이터셋을 이용해 얼마나 올바르게 값을 추정하는 가를 알아봅니다.

In [28]: x, t = get_data()
   ....: network = init_network()
   ....: 
   ....: accuracy_cnt = 0
   ....: for i in range(len(x)):
   ....:   y = predict(network, x[i])
   ....:   p = np.argmax(y)
   ....:   if p == t[i]:
   ....:     accuracy_cnt += 1
   ....: 
   ....: print("정확도: {}".format(accuracy_cnt / len(x)))
   ....: 
정확도: 0.9352

accuracy_cnt는 실제값과 추정된 값이 일치하는 갯수를 세는 변수입니다. np.argmax() 함수는 배열 중에서 가장 큰 값에 해당하는 인덱스를 반환합니다.

배치 처리

앞에서는 이미지 하나씩 값을 추정했습니다.

_images/nn_mnist_array1.png

이미지 여러 장을 한 번에 계산하면 더 효율적입니다. 다음 그림과 같이 100개의 이미지를 한 번에 처리하며 출력값을 100x10 형태가 됩니다.

_images/nn_mnist_array100.png

이와 같이 한 번에 여러 개의 데이터를 처리하는 것을 배치(batch) 처리라고 합니다.

In [29]: x, t = get_data()
   ....: network = init_network()
   ....: 
   ....: batch_size = 100
   ....: accuracy_cnt = 0
   ....: 
   ....: for i in range(0, len(x), batch_size):
   ....:   x_batch = x[i:i+batch_size]
   ....:   y_batch = predict(network, x_batch)
   ....:   p = np.argmax(y_batch, axis=1)
   ....:   accuracy_cnt += np.sum(p == t[i:i+batch_size])
   ....: 
   ....: print("정확도: {}".format(accuracy_cnt / len(x)))
   ....: 
정확도: 0.9352

연습문제

  1. 다음 표를 만족하는 2층 퍼셉트론을 구현해 보세요. 즉, 다음 식을 만족하는 \(w_1, w_2, b\)를 구해서 파이썬 함수로 만들어 보세요.

    \[\begin{split}y = h(a)\\ h(a) = \begin{cases} 0, & \text{if} \quad a \le 0 \\ 1, & \text{if} \quad a > 0 \end{cases} \\ a_i^{(j)} = w_{i1}^{(j)} x_1 + w_{i2}^{(j)} x_2 + b_i^{(j)}\end{split}\]

    \(x_1\)

    \(x_2\)

    \(y\)

    1

    1

    1

    -1

    1

    0

    -1

    -1

    1

    1

    -1

    0

    1

    2

    0

    		 
    In [30]: x1 = np.array([1, -1, -1, 1, 1])
   ....: x2 = np.array([1, 1, -1, -1, 2])
   ....: 
   ....: import matplotlib.pyplot as plt
   ....: fig = plt.figure()
   ....: ax = fig.add_subplot(111)
   ....: c_list = ['r', 'b', 'r', 'b', 'b']
   ....: ax.scatter(x1, x2, marker='o', c=c_list)
   ....: ax.set_xlim([-2, 2])
   ....: ax.grid()
   ....: ax.set_aspect('equal')
   ....: ax.axhline()
   ....: ax.axvline()
   ....: 
Out[30]: <matplotlib.lines.Line2D at 0x1f50de39e50>
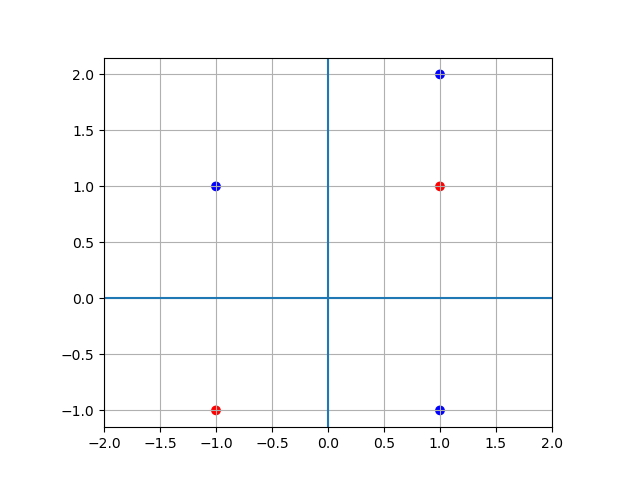
    _images/plot_nn_exercise1.png

  2. 다음 표를 만족하는 2층 퍼셉트론을 구현해 보세요. 즉, 다음 식을 만족하는 \(w_1, w_2, b\)를 구해서 파이썬 함수로 만들어 보세요.

    \[\begin{split}y = h(a)\\ h(a) = \begin{cases} 0, & \text{if} \quad a \le 0 \\ 1, & \text{if} \quad a > 0 \end{cases} \\ a_i^{(j)} = w_{i1}^{(j)} x_1 + w_{i2}^{(j)} x_2 + b_i^{(j)}\end{split}\]

    \(x_1\)

    \(x_2\)

    \(y\)

    1

    1

    1

    -1

    1

    0

    -1

    -1

    1

    1

    -1

    0

    0

    0

    0

    		 
    In [32]: x1 = np.array([1, -1, -1, 1, 0])
   ....: x2 = np.array([1, 1, -1, -1, 0])
   ....: 
   ....: import matplotlib.pyplot as plt
   ....: fig = plt.figure()
   ....: ax = fig.add_subplot(111)
   ....: c_list = ['r', 'b', 'r', 'b', 'b']
   ....: ax.scatter(x1, x2, marker='o', c=c_list)
   ....: ax.set_xlim([-2, 2])
   ....: ax.set_ylim([-2, 2])
   ....: ax.grid()
   ....: ax.set_aspect('equal')
   ....: ax.axhline()
   ....: ax.axvline()
   ....: 
Out[32]: <matplotlib.lines.Line2D at 0x1f50dfccb80>
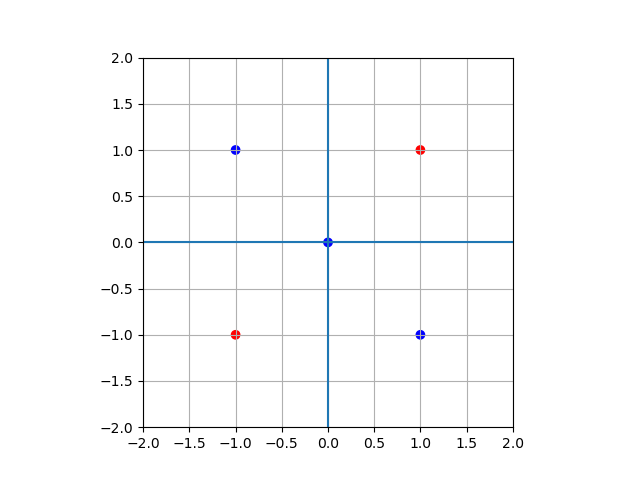
    _images/plot_nn_exercise2.png

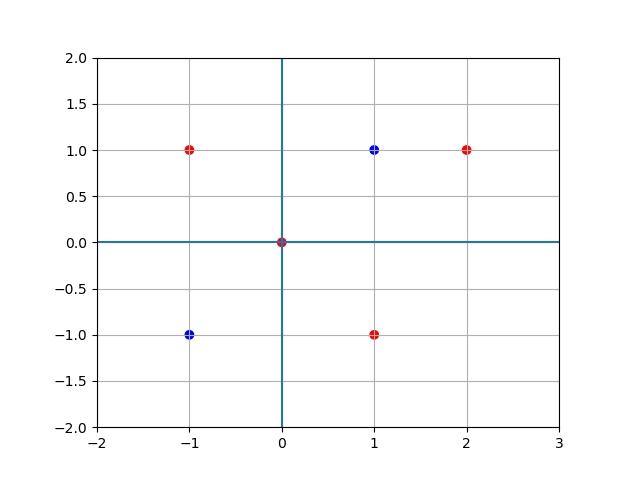
  3. 다음 표를 만족하는 2층 퍼셉트론을 구현해 보세요. 즉, 다음 식을 만족하는 \(w_1, w_2, b, p\)를 구해서 파이썬 함수로 만들어 보세요.

    \[\begin{split}y = h(a)\\ h(a) = \begin{cases} 0, & \text{if} \quad |a| \le p \\ 1, & \text{if} \quad |a| > p \end{cases} \\ a_i^{(j)} = w_{i1}^{(j)} x_1 + w_{i2}^{(j)} x_2 + b_i^{(j)}\end{split}\]

    \(x_1\)

    \(x_2\)

    \(y\)

    1

    1

    0

    -1

    1

    1

    -1

    -1

    0

    1

    -1

    1

    0

    0

    1

    2

    1

    1

    		 
    In [34]: x1 = np.array([1, -1, -1, 1, 0, 2])
   ....: x2 = np.array([1, 1, -1, -1, 0, 1])
   ....: 
   ....: import matplotlib.pyplot as plt
   ....: fig = plt.figure()
   ....: ax = fig.add_subplot(111)
   ....: c_list = ['b', 'r', 'b', 'r', 'r', 'r']
   ....: ax.scatter(x1, x2, marker='o', c=c_list)
   ....: ax.set_xlim([-2, 3])
   ....: ax.set_ylim([-2, 2])
   ....: ax.grid()
   ....: ax.set_aspect('equal')
   ....: ax.axhline()
   ....: ax.axvline()
   ....: 
Out[34]: <matplotlib.lines.Line2D at 0x1f50ce43f70>
    _images/plot_nn_exercise3.png

연습문제 풀이