합성곱 신경망¶
전체 구조¶
이전까지 신경망은 계층의 모든 뉴런과 결합되어 있습니다. 이것을 완전연결(fully connected) 계층이라 하며 어파인(Affine) 계층으로 구현했습니다.
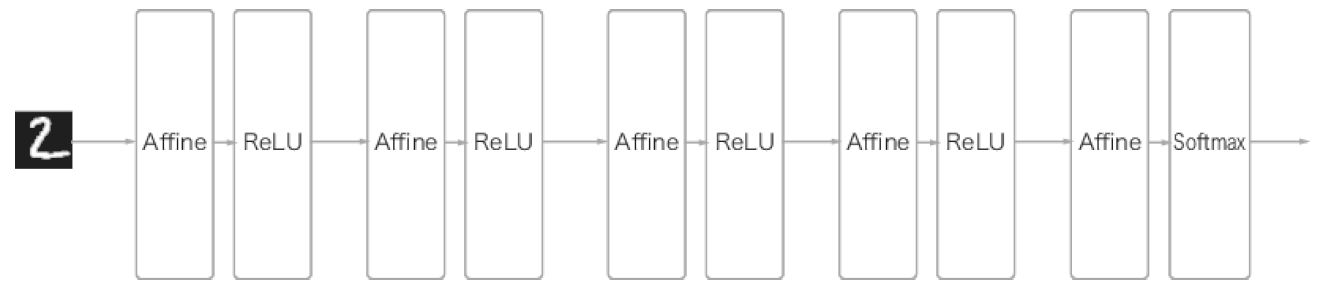
CNN은 합성곱(Convolution) 계층과 풀링(Pooling) 계층이 추가됩니다.

합성곱 계층¶
CNN에서는 패딩(padding), 스트라이드(stride) 등의 용어가 등장합니다.
완전연결 계층의 문제점¶
- 데이터의 형태가 무시됩니다.
공간적 정보가 무시됩니다.
합성곱 연산¶
합성곱 연산은 이미지 처리에서 필터(또는 커널) 연산에 해당합니다.
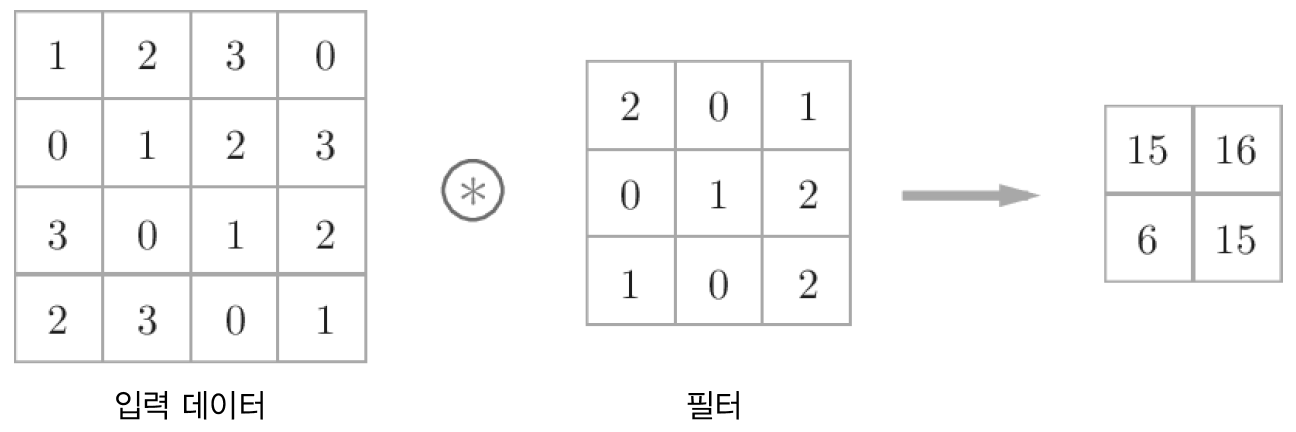
합성곱 연산의 예¶
합성곱 연산은 필터의 윈도우(window)를 일정 간격으로 이동하며 입력과 필터에 대응하는 원소끼리 곱한 후 총합을 구하는 것입니다. 이러한 계산을 단일 곱셈-누산(fused multiply-add, FMA)이라 합니다.
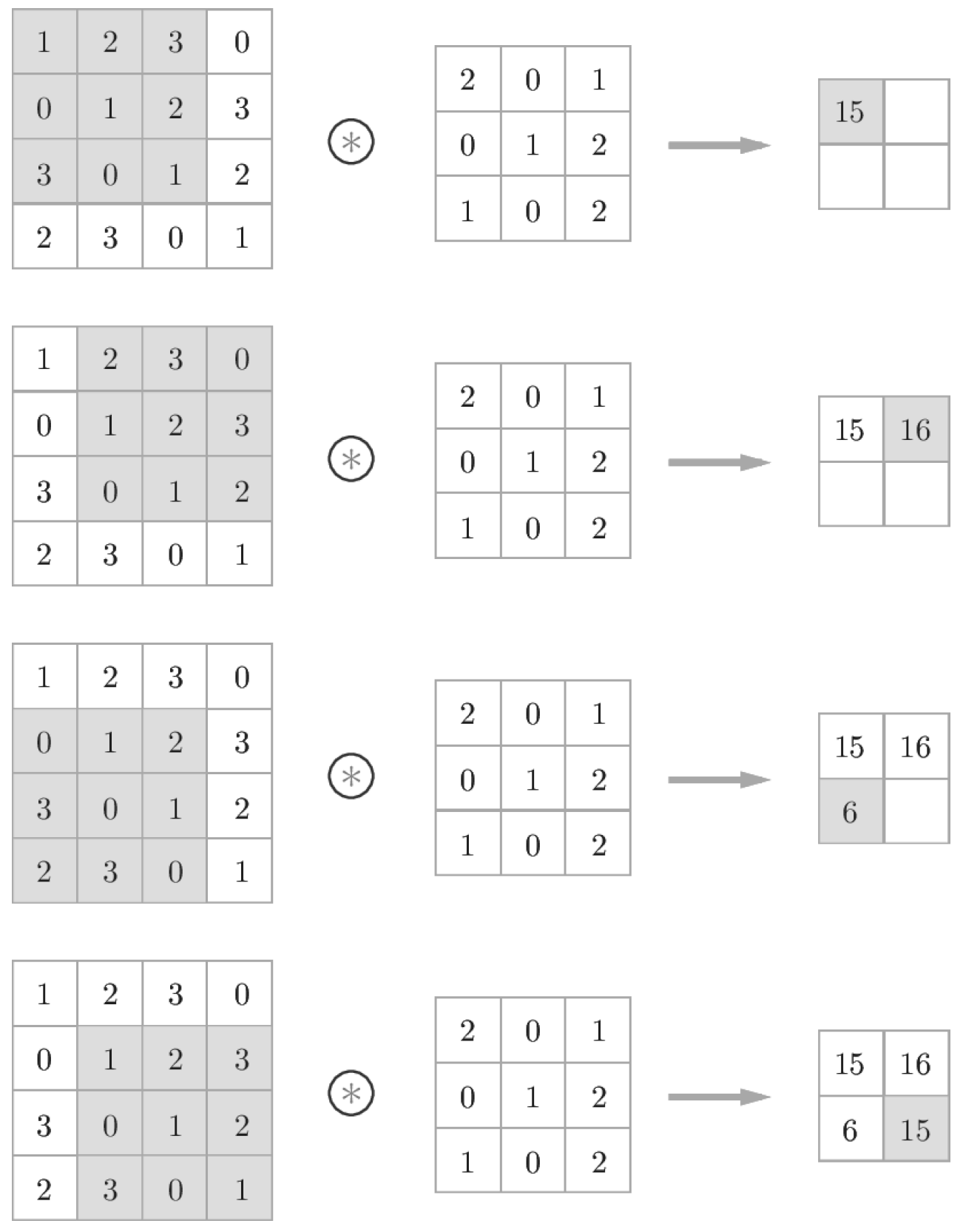
합성곱 연산 계산 순서¶
완전연결 신경망에 가중치 매개변수와 편향이 존재하는데 CNN에서는 가중치 매개변수에 해당하는 것이 필터의 매개변수입니다. 그리고 CNN에도 편향이 존재합니다.
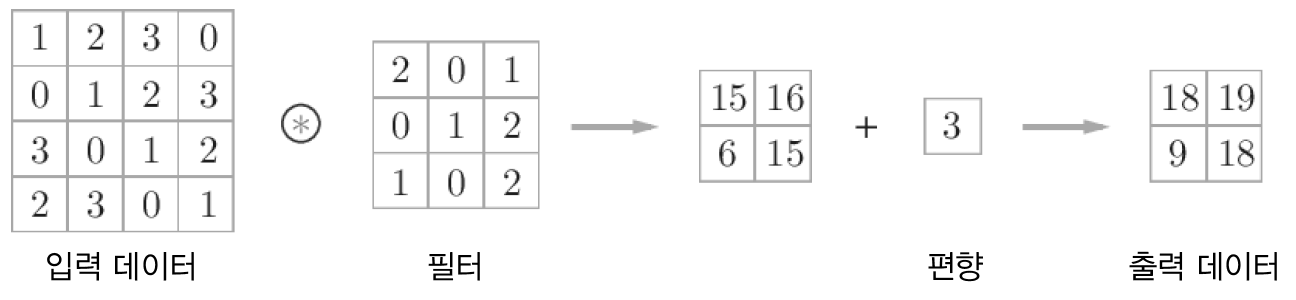
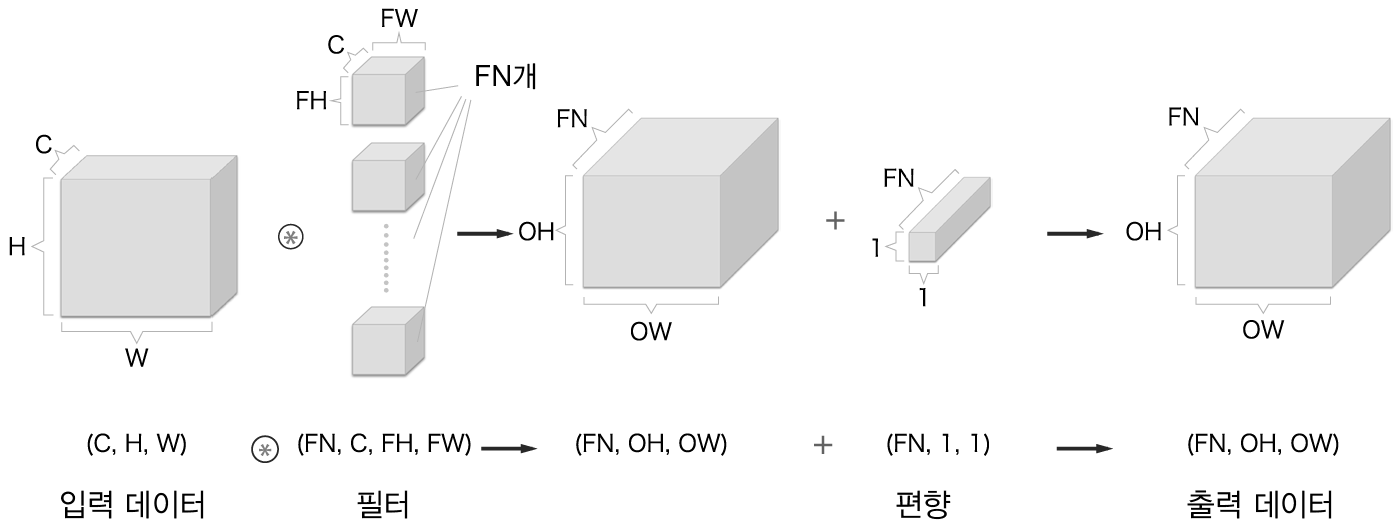
합성곱 연산의 편향¶
패딩¶
합성곱 연산을 수행하기 전에 입력 데이터 주변에 특정 값을 채우는 것을 패딩(padding)이라고 합니다.
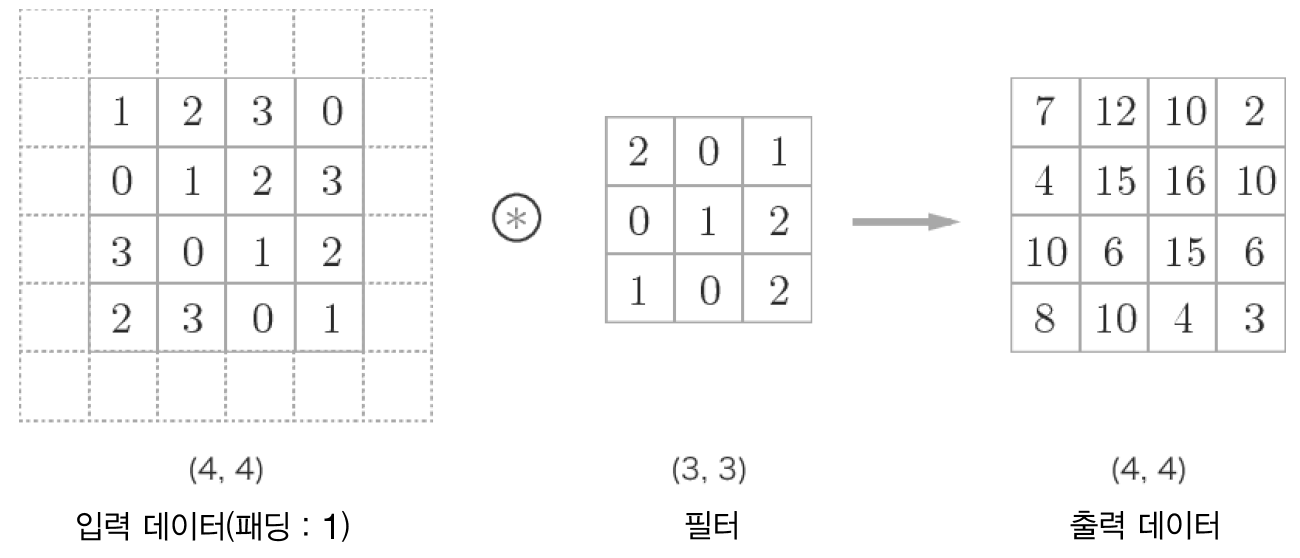
합성곱 연산의 패딩(점선 부분이 패딩입니다.)¶
패딩은 주로 출력 크기를 조정할 목적으로 사용합니다.
넘파이에서는 배열의 패딩을 처리할 수 있는 함수 np.pad를 제공합니다. 파이썬 기초의 패딩을 참조하기 바랍니다.
스트라이드¶
필터를 적용하는 위치의 간격을 스트라이드(stride)라고 합니다.
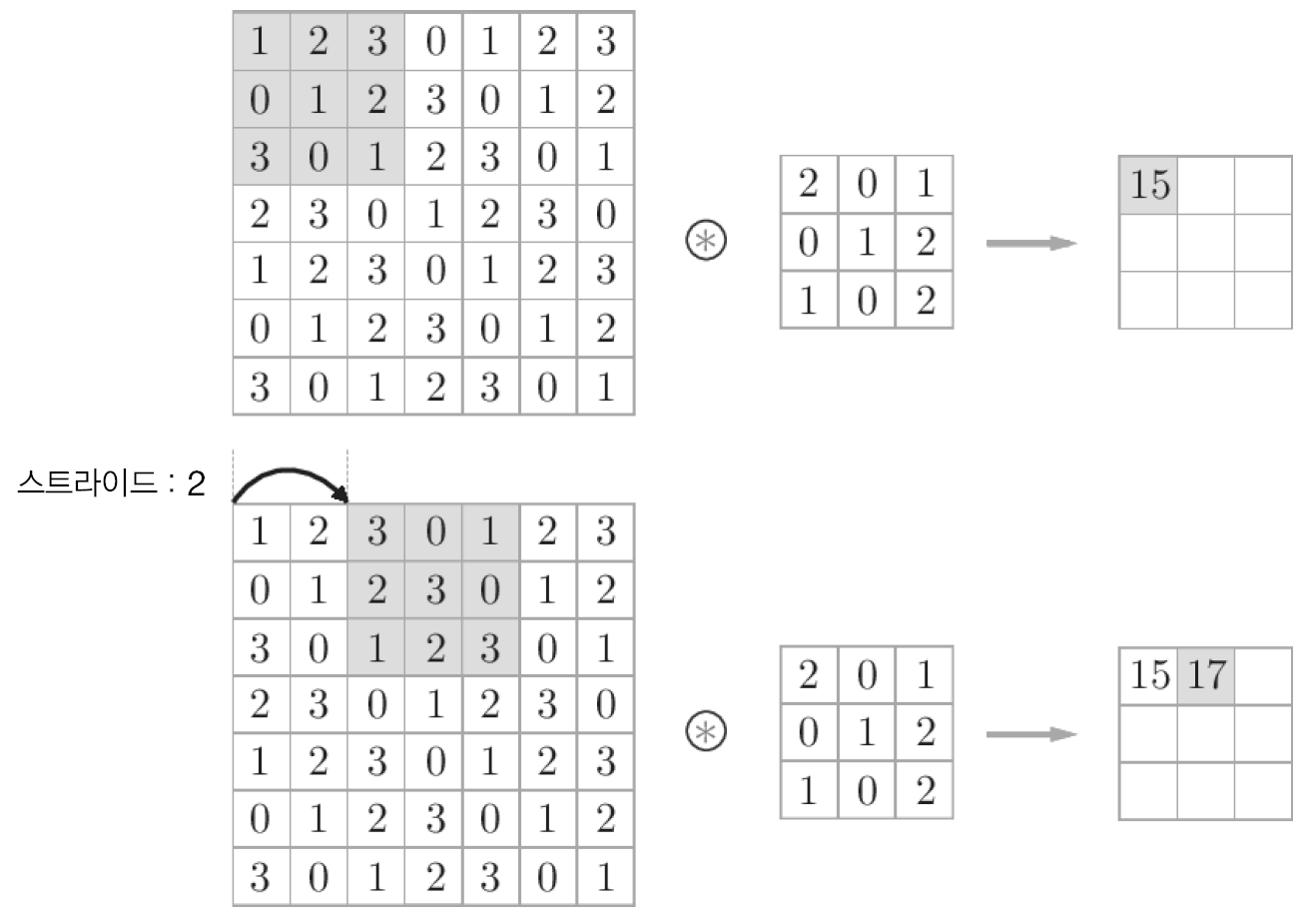
스트라이드가 2인 합성곱 연산¶
입력 크기를 (H, W), 필터 크기를 (FH, FW), 출력크기를 (OH, OW), 패딩을 P, 스트라이드를 S라 하면 출력크기는 다음과 같이 계산됩니다.
3차원 데이터의 합성곱 연산¶
일반적으로 이미지는 이미지의 크기인 세로, 가로 뿐아니라 색상에 대한 정보인 채널(channel)이 포함되는 3차원 데이터입니다.
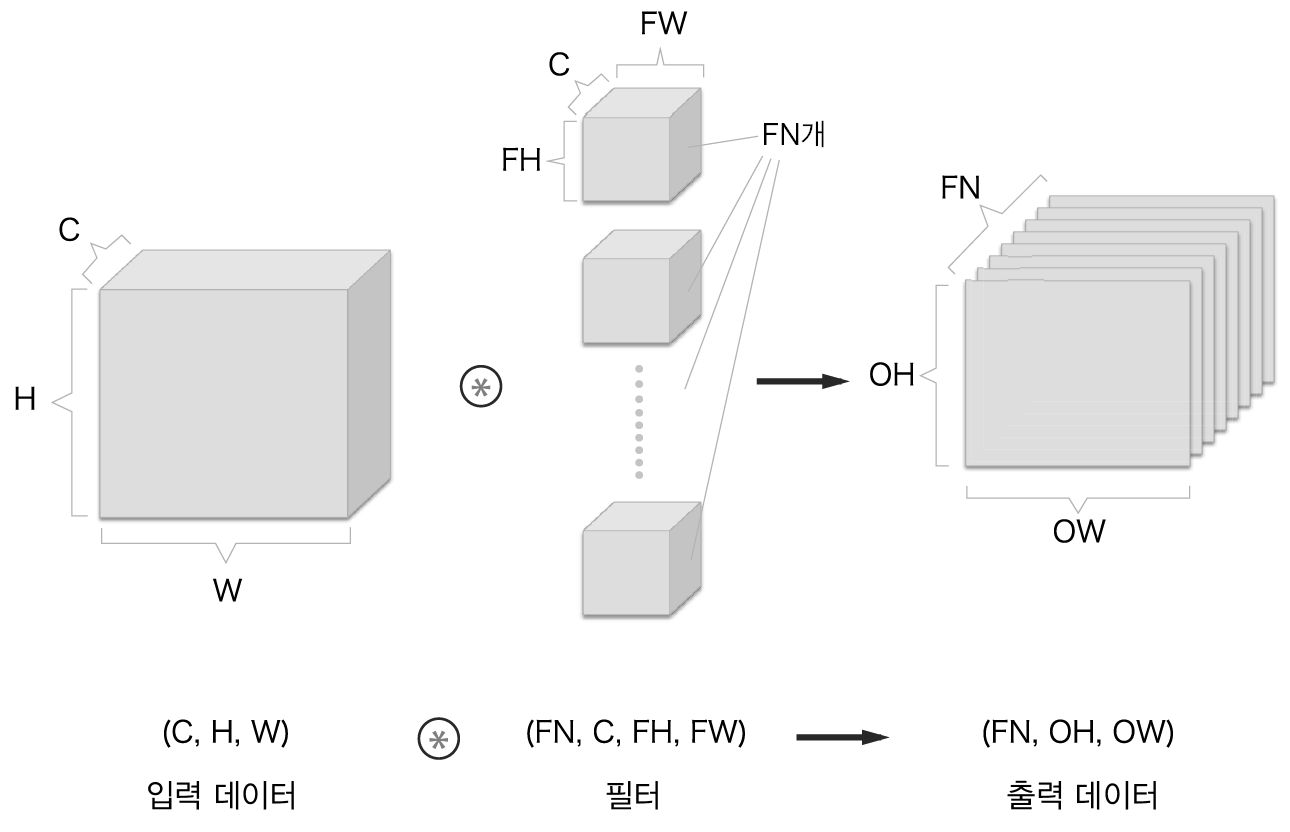
채널이 여러 개 있을 때 입력 데이터와 필터의 합성곱 연산을 채널마다 수행하고, 그 결과를 더해서 하나의 출력을 얻습니다.
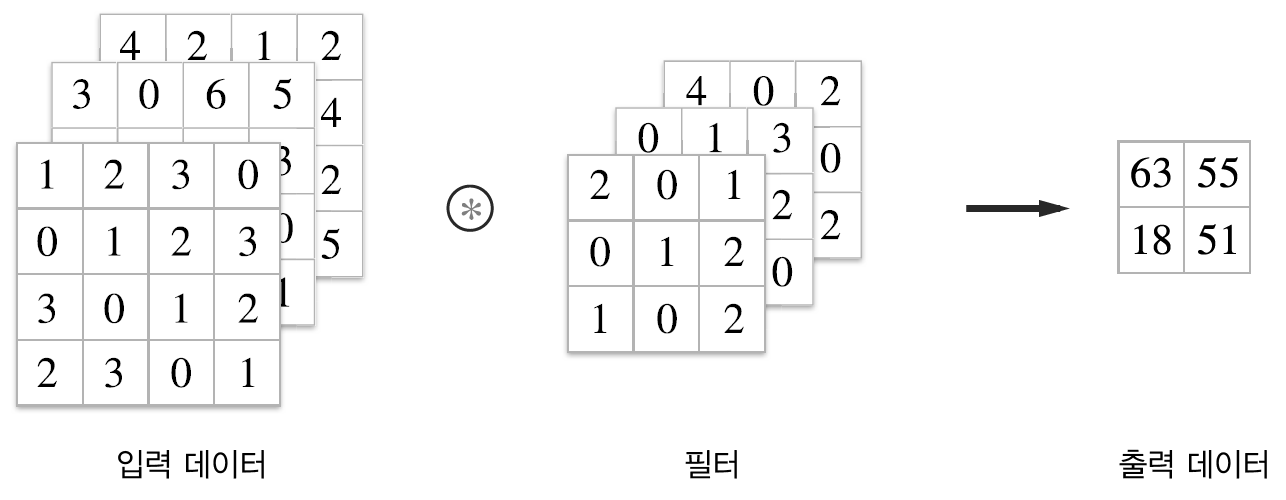
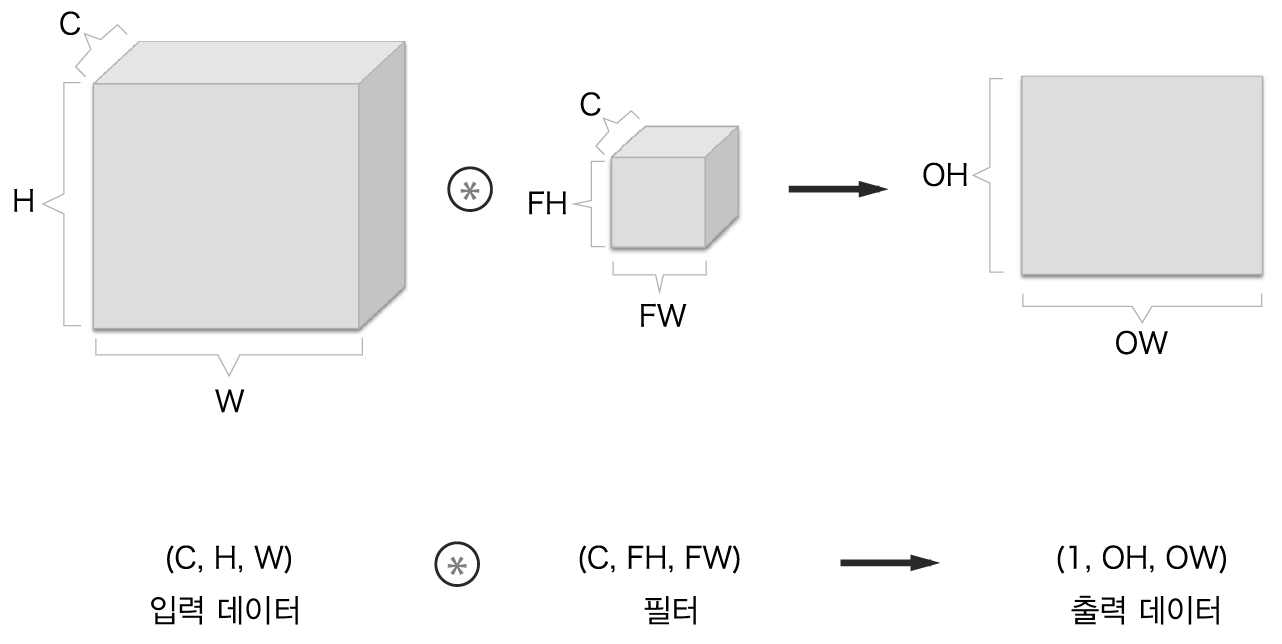
3차원 데이터 합성곱 연산의 예¶
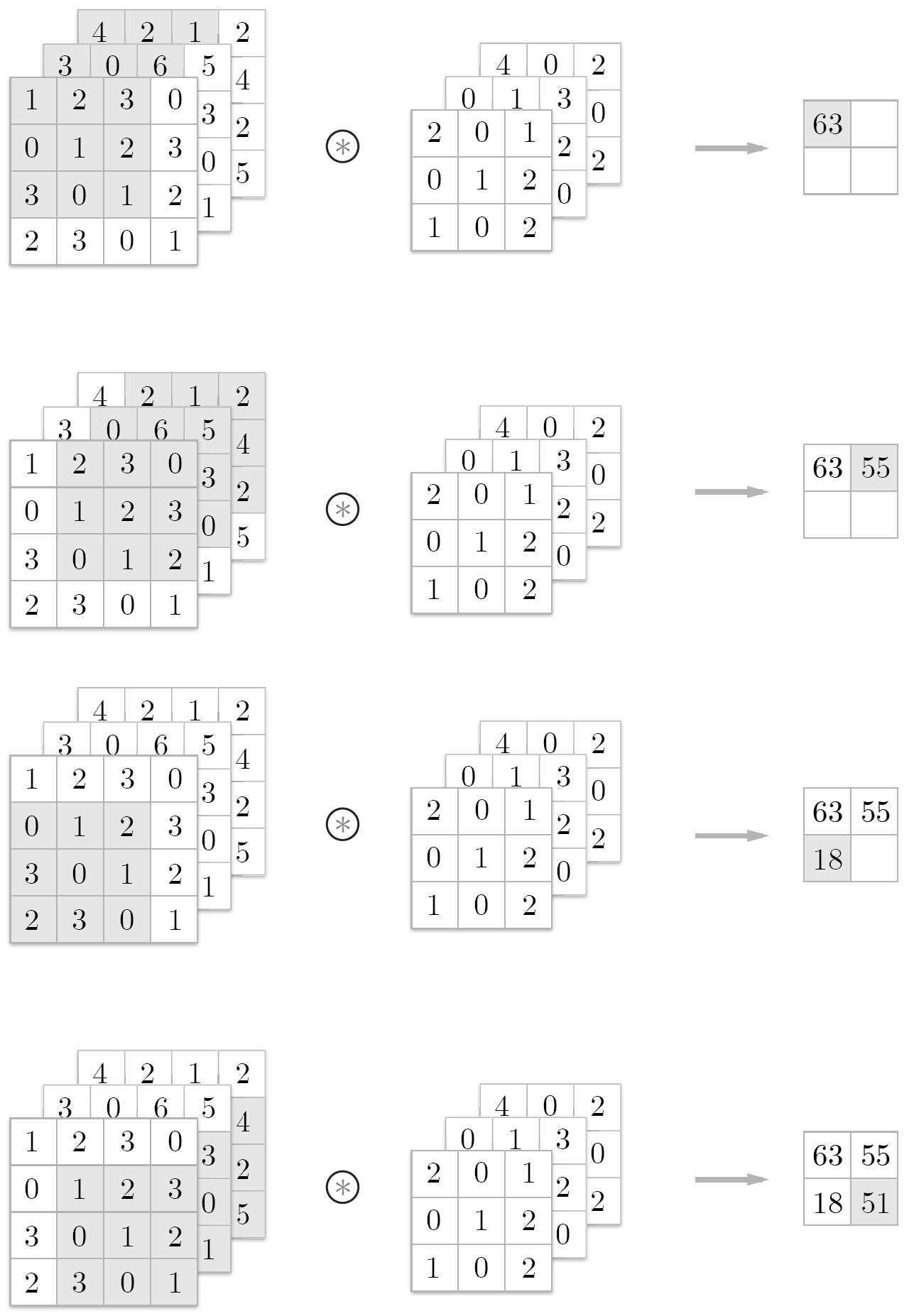
3차원 데이터 합성곱 연산의 계산 순서¶
풀링 계층¶
풀링은 세로, 가로 방향의 공간을 줄이는 연산입니다.
다음 그림은 2x2 최대 풀링(max pooling)을 스트라이드 2로 처리하는 순서입니다. 최대 풀링은 대상 영역에서 최댓값을 구하는 연산입니다. 풀링의 스트라이드는 윈도우 크기와 같은 값으로 설정하는 것이 일반적입니다.
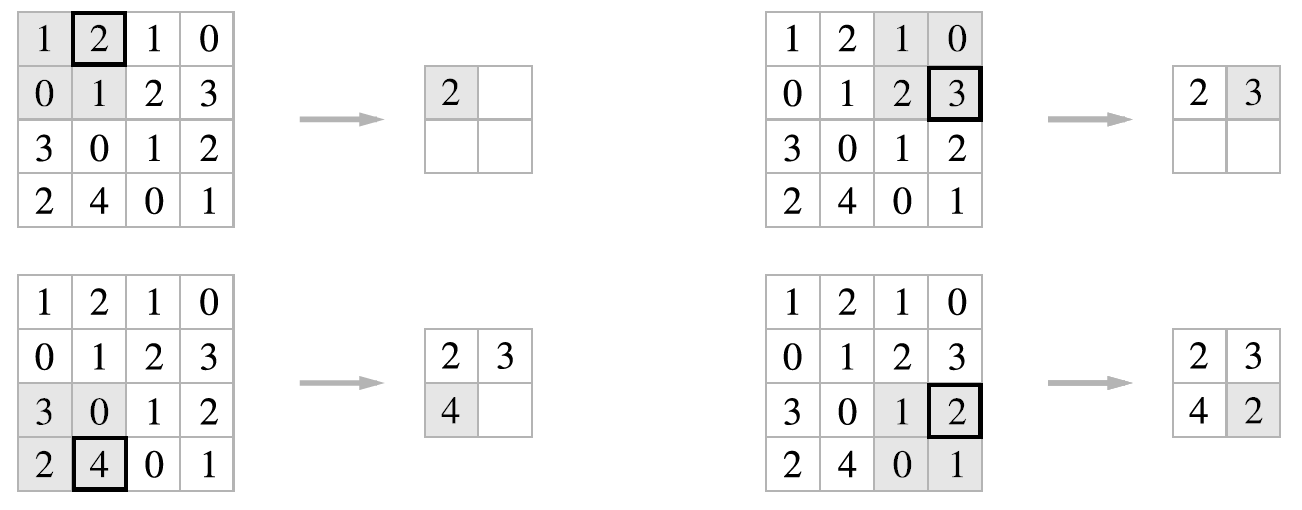
최대 풀링의 처리 순서¶
풀링은 최대 풀링 외에도 평균 풀링(average pooling) 등이 있습니다. 이미지 인식 분야에서는 주로 최대 풀링을 사용합니다. 여기서도 풀링 계층이라고 하면 최대 풀링을 의미합니다.
최대 풀링을 함수로 표현하고 편미분을 하면 다음과 같습니다.
따라서 최대 풀링을 이용한 역전파를 할 때는 최대값에 해당하는 변수만 1 이고 나머지는 0이 됩니다.
평균 풀링을 함수로 표현하고 편미분을 하면 다음과 같습니다.
풀링 계층의 특징¶
- 학습해야 할 매개 변수가 없다.
합성곱 계층과 달리 풀링계층는 학습해야할 매개변수가 없습니다.
- 채널수가 변하지 않는다
풀링연산은 입력 데이터의 채널 수 그대로 출력데이터로 보냅니다.
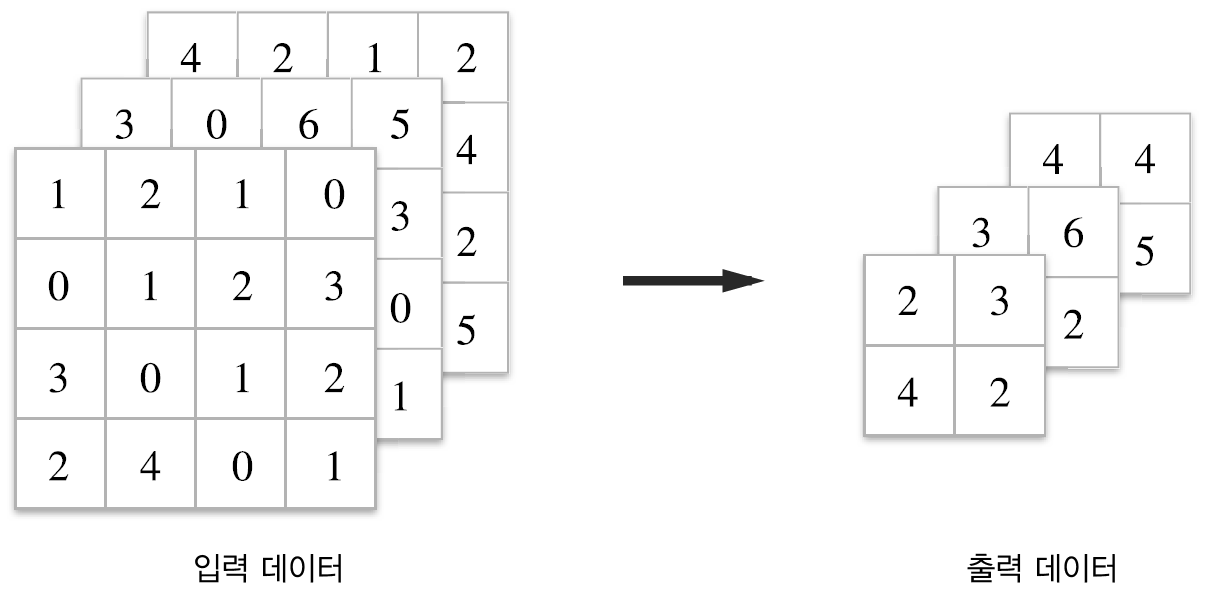
- 입력의 변화에 영향을 적게 받는다
입력데이터가 조금 변해도 풀링의 결과는 잘 변하지 않습니다. 다음 그림에서 보는 바와 같이 입력 데이터가 오른쪽으로 1칸씩 이동을 해도 값이 변하지 않는 것을 알 수 있습니다.
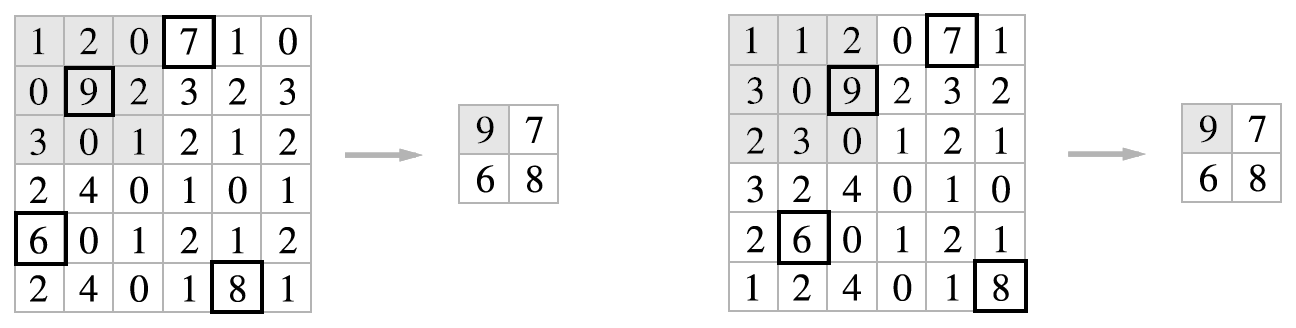
합성곱/풀링 계층 구현¶
4차원 배열¶
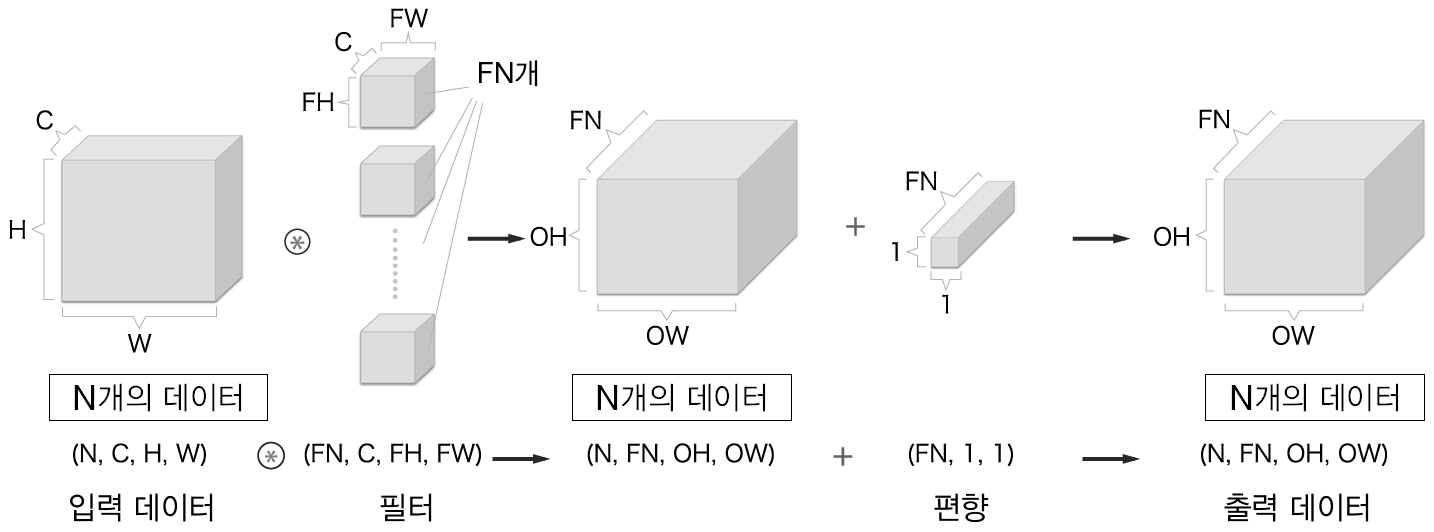
CNN에서 데이터는 4차원입니다. 입력데이터는 (N, C, H, W)로 N은 입력데이터의 수, C는 채널의 수, H, W는 각각 높이와 너비입니다.
im2col으로 데이터 전개¶
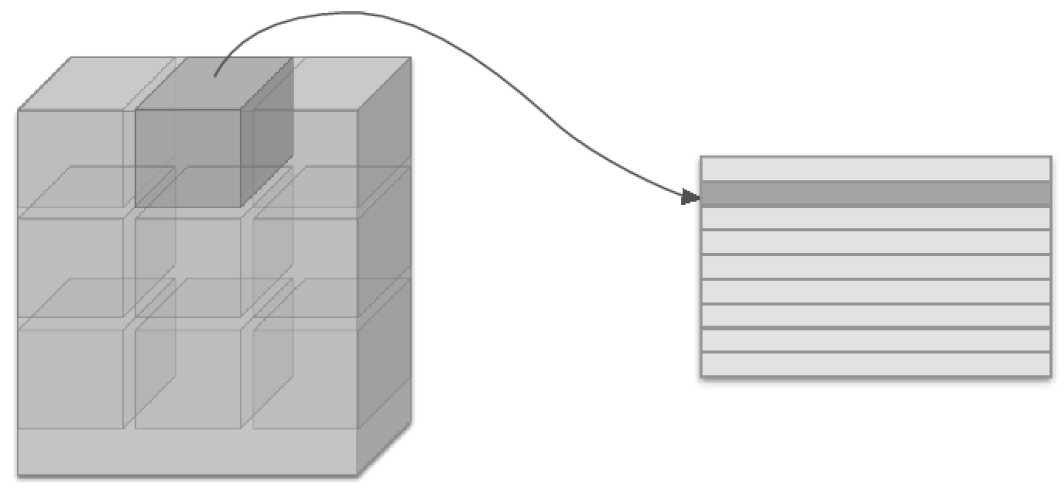
입력데이터를 im2col 을 이용하여 2차원 데이터로 변환하는 것입니다. 변환된 2차원 데이터의 열의 갯수는 필터를 일렬로 나열한 것의 갯수와 같도록 맞춥니다.
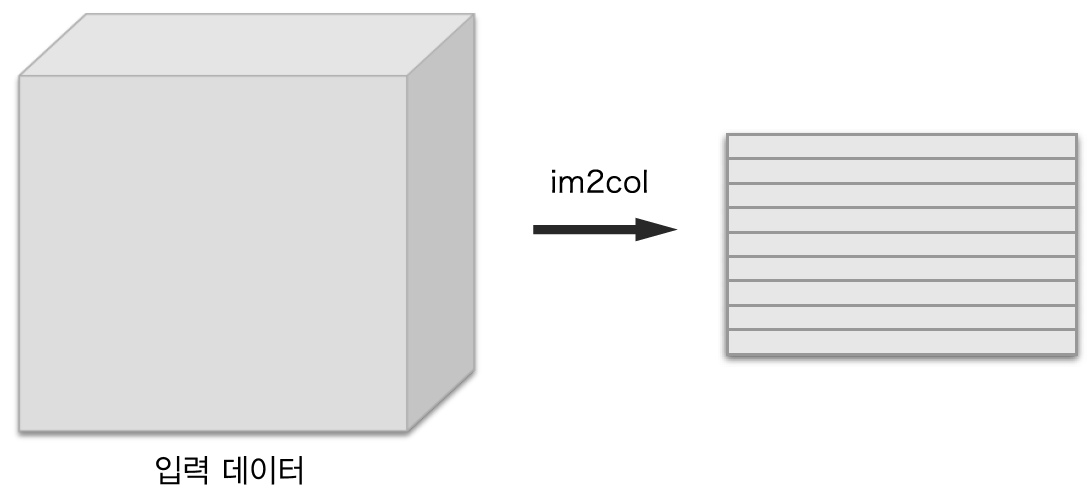
N 개의 입력데이터에 대해서 모두 2차원 데이터 형태로 변경합니다. 2차원 데이터의 행의 갯수는 N * OH * OW 이고 열의 갯수는 C * FH * FW 개 입니다.
각각의 필터를 하나의 열을 차지 하도록 2차원 데이터로 변환합니다. 필터의 크기는 행의 갯수는 C * FH * FW 이고 열의 갯수는 필터의 갯수인 FN이 됩니다. 그러므로 앞에서 변경된 2차원 입력데이터와 2차원 필터 데이터와 행렬곱을 해서 합성곱 연산 결과를 얻습니다. 합성곱해서 최종적으로 나오는 출력데이터의 크기는 (N, OH, OW, FN) 입니다.
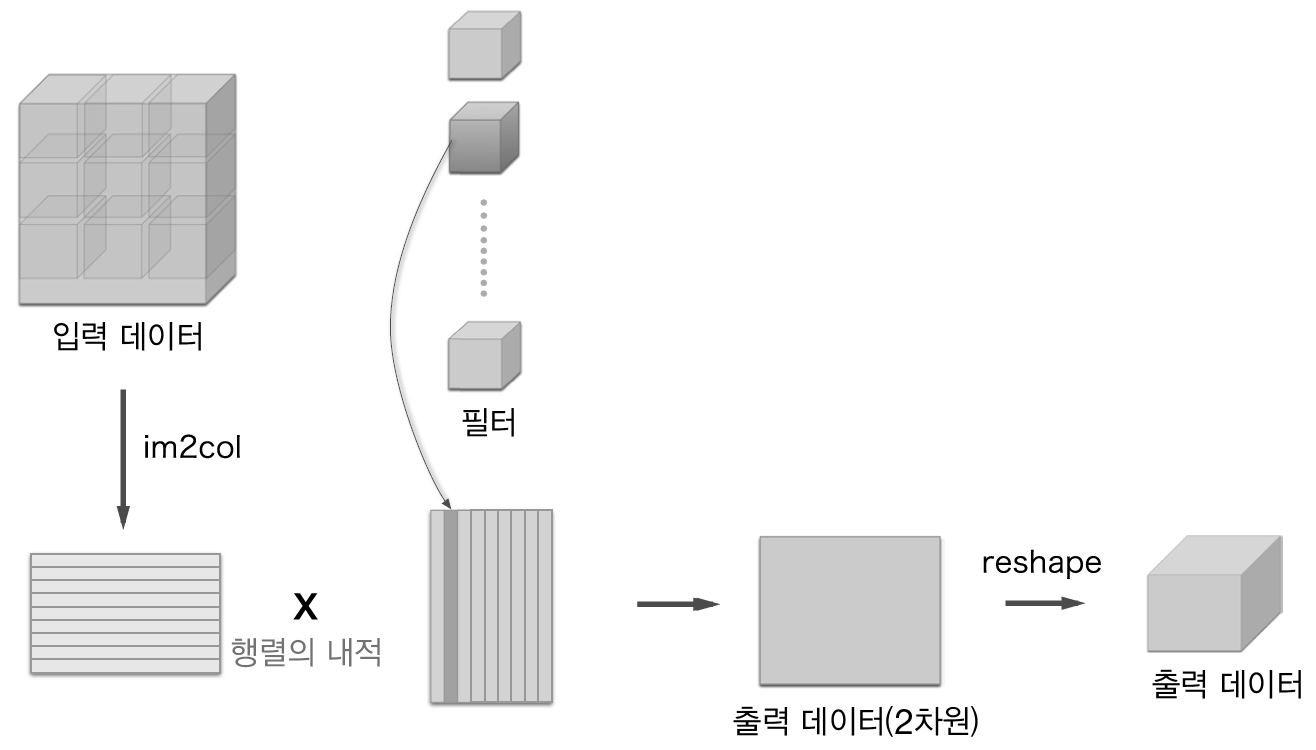
합성곱 연산을 하려면 중첩 for 문이 필요합니다. 여기서는 for 문 대신 im2col 함수를 이용합니다. im2col 함수는 입력데이터를 필터링 계산을 편하게 4차원 데이터를 2차원으로 변환합니다.
In [1]: def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
...: """
...:
...: Parameters
...: ----------
...: input_data : (데이터 수, 채널 수, 높이, 너비)의 4차원 배열로 이루어진 입력데이터
...: filter_h : 필터의 높이
...: filter_w : 필터의 너비
...: stride : 스트라이드
...: pad : 패딩
...:
...: Returns
...: -------
...: col : 2차원 배열
...: """
...:
...: N, C, H, W = input_data.shape
...: out_h = (H + 2 * pad - filter_h) // stride + 1
...: out_w = (W + 2 * pad - filter_w) // stride + 1
...:
...: img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
...: col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
...:
...: for y in range(filter_h):
...: y_max = y + stride * out_h
...: for x in range(filter_w):
...: x_max = x + stride * out_w
...: col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
...:
...: col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
...: return col
...:
np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')에서input_data배열에 패딩을 추가합니다.N,C차원에는 패딩을 넣지 않고H,W차원에 각각 앞, 뒤로pad갯수 만큼의 기본값0을 넣습니다.col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]에서y, x는 필터의 인덱스를 의미합니다. 필터y, x부분과 대응하는 이미지 셀들img[:, :, y:y_max:stride, x:x_max:stride]만 골라서 추가합니다.y:y_max:stride는 출력데이터 크기OH만큼에 해당하는 이미지 셀들만 골라내는 겁니다.col.transpose(0, 4, 5, 1, 2, 3)으로N, OH, OW, C, FH, FW축의 배열로 변경합니다.col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)을 이용하여(N * OH * OW, C * FH * FW)크기로 2차원 배열로 변경합니다.
col2im¶
역전파시 순전파 때의 입력데이터에 맞도록 데이터의 크기를 원래 크기에 맞도록 되돌릴 필요가 있습니다. 이때 col2im 함수를 사용하여 되돌립니다.
In [2]: def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
...: """
...:
...: Parameters
...: ----------
...: col : 변경할 데이터
...: input_shape : 원래 입력데이터 크기(예:(10, 1, 28, 28))
...: filter_h : 필터 높이
...: filter_w : 필터 너비
...: stride : 스트라이드
...: pad : 패딩
...:
...: Returns
...: -------
...: img : 원래 4차원 배열 이미지
...: """
...:
...: N, C, H, W = input_shape
...: out_h = (H + 2 * pad - filter_h)//stride + 1
...: out_w = (W + 2 * pad - filter_w)//stride + 1
...: col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
...:
...: img = np.zeros((N, C, H + 2 * pad + stride - 1, W + 2 * pad + stride - 1))
...: for y in range(filter_h):
...: y_max = y + stride * out_h
...: for x in range(filter_w):
...: x_max = x + stride * out_w
...: img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
...:
...: return img[:, :, pad:H + pad, pad:W + pad]
...:
col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)을 이용하여 2차원 데이터를 6차원 데이터(N, C, FH, FW, OH, OW)로 변경합니다.H + 2 * pad + stride - 1가 나오는 이유는 다음과 같습니다.y_max의 최대값은y가filter_h - 1일 때이므로img[:, :, y, x]에서y의 값의 법위는0부터y_max = filter_h - 1 + stride * out_h입니다. 그리고out_h = (H + 2 * pad - filter_h) // stride + 1식으로부터filter_h - 1 + stride * out_h = H + 2 * pad + stride - 1이 됩니다.img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]에서im2col에서 했던 것과 역으로 하는데+=연산을 하여, 기존에 있던 원소에 더하는 과정을 실행합니다. 이것은 편미분할 때 같은 변수에 대해서 각각 여러 번 했던 것을 합치는 과정이 들어간 겁니다.img[:, :, pad:H + pad, pad:W + pad]은 패딩 부분을 제외한 원래 이미지(N, C, H, W)를 반환합니다.
합성곱 계층 구현¶
In [3]: class Convolution:
...: def __init__(self, W, b, stride=1, pad=0):
...: self.W = W # 필터
...: self.b = b
...: self.stride = stride
...: self.pad = pad
...:
...: # 중간데이터(backward때 사용)
...: self.x = None
...: self.col = None
...: self.col_W = None
...:
...: # 가중치
...: self.dW = None
...: self.db = None
...:
...: def forward(self, x):
...: FN, C, FH, FW = self.W.shape
...: N, C, H, W = x.shape
...: out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
...: out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
...:
...: col = im2col(x, FH, FW, self.stride, self.pad)
...: col_W = self.W.reshape(FN, -1).T # 필터 전개
...:
...: out = np.dot(col, col_W) + self.b
...: out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
...:
...: self.x = x
...: self.col = col
...: self.col_W = col_W
...:
...: return out
...:
...: def backward(self, dout):
...: FN, C, FH, FW = self.W.shape
...: dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
...:
...: self.db = np.sum(dout, axis=0)
...: self.dW = np.dot(self.col.T, dout)
...: self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
...:
...: dcol = np.dot(dout, self.col_W.T)
...: dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
...:
...: return dx
...:
순전파
col = im2col(x, FH, FW, self.stride, self.pad)을 이용하여 4차원 입력데이터x를 2차원 배열col으로 변경합니다.col의 크기는(N * OH * OW, C * FH * FW)입니다.col_W = self.W.reshape(FN, -1).T를 이용하여col_W는(C * FH * FW, FN)형태로 변환됩니다.out = np.dot(col, col_W) + self.b에서 행렬곱 연산을 합니다.out의 크기는(N * OH * OW, FN)이 됩니다.편향
self.b의 크기는(FN,)이었는데out배열의 크기만큼 브로드캐스팅을 하여 더합니다.out = out.reshape(N, out_h, out_w, -1)를 이용하여(N, OH, OW, FN)배열로 만들고transpose(0, 3, 1, 2)를 통하여(N, FN, OH, OW)크기의 배열을 만들어 반환합니다.역전파
backward()과정에서 사용하기 위하여self.x,self.col,self.col_W를 보존합니다.
다음 그림은 transpose 과정을 표현한 것입니다.
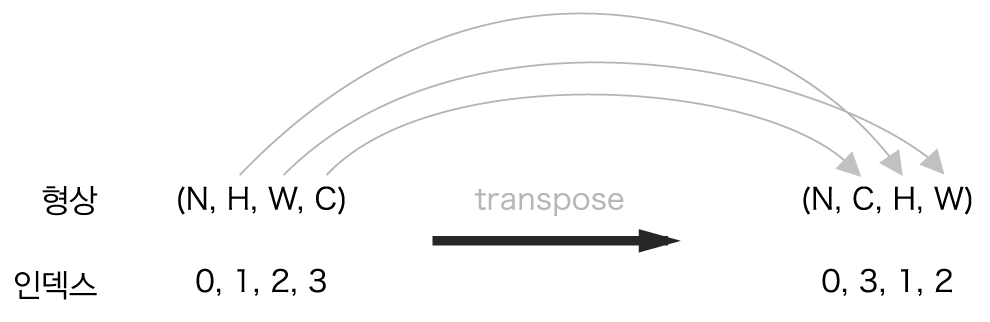
위 그림에서 C는 FN으로 수정합니다.
CNN의 순전파는 어파인 계층과 같은 상태로 전파되는 것을 알 수 있습니다. col 은 어파인의 X 와 col_W은 어파인에서 W와 대응됩니다. Affine/Softmax 계층 구현을 참조하세요.
역전파
CNN의 역전파는 순전파에서 어파인 계층과 비슷했던 것과 같이 어파인 역전파와 비슷한 과정으로 진행됩니다. 즉, col이 X에 대응되고, col_W가 W에 대응되므로 어파인에서 dx, dW, db를 계산하는 것과 같이 계산한 후에 원래 크기에 맞춰 변형만 해주면 됩니다. 마찬가지로 역전파 Affine/Softmax 계층 구현을 참조하세요.
역전파로 입력되는
dout의 크기는 순전파 출력과 같은 크기인(N, FN, OH, OW)입니다.dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)를 이용하여(N * OH * OW, FN)형태로 변환합니다.self.db = np.sum(dout, axis=0)은 어파인의db를 구하는 과정과 같습니다.self.dW = np.dot(self.col.T, dout)은 어파인의dW를 구하는 과정과 같고self.col = (N * OH * OW, C * FH * FW)은 어파인의X와 같은 역할을 합니다.self.dW의 크기는(C * FH * FW, FN)이 됩니다.self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)를 이용하여self.dW를(FN, C, FH, FW)형태로 변환합니다.dcol = np.dot(dout, self.col_W.T)을 이용하여 어파인의dx에 대응하는 연산을 수행합니다.col_W가 어파인의W와 대응됩니다.dout의 크기는(N * OH * OW, FN)이고col_W.T는(FN, C * FH * FW)이므로 행렬곱dcol의 결과는(N * OH * OW, C * FH * FW)입니다.col2im를 통해서 순전파 때 입력되었던 입력데이터의 크기로 역전파dx가 반환됩니다.col2im에서 설명했듯이 이 과정에서 중복된 편미분들이 합쳐지게 됩니다.
풀링 계층 구현¶
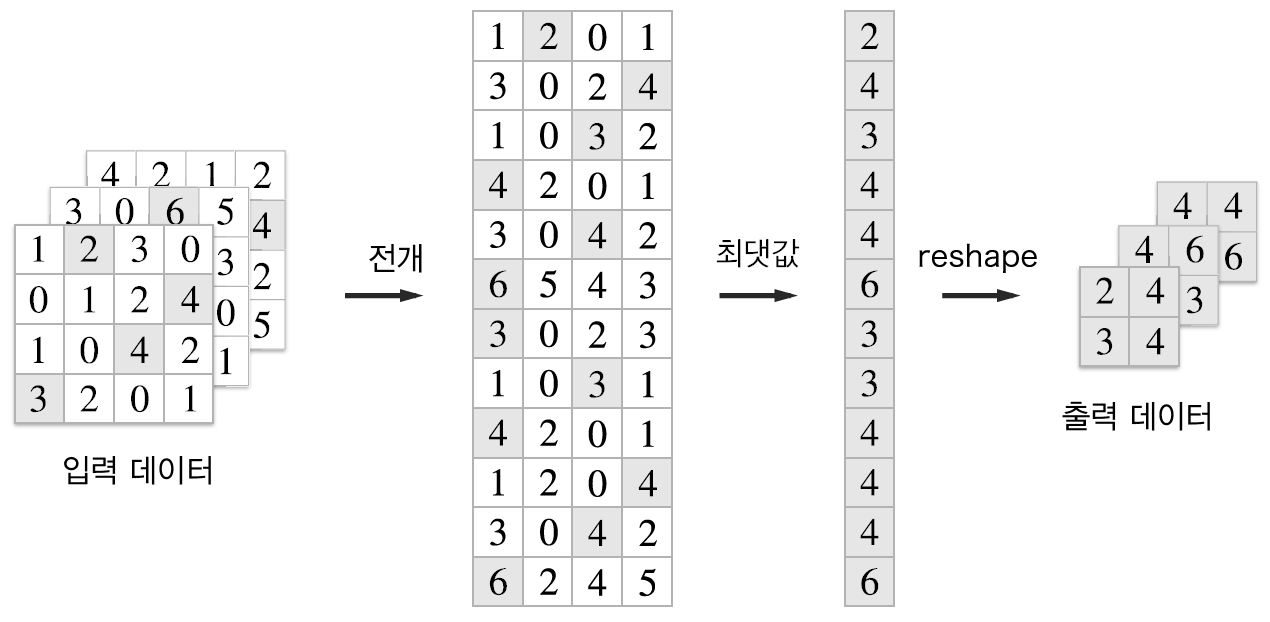
합성곱 계층에서와 마찬가지로 4차원 데이터를 im2col을 이용하여 2차원 데이터로 변환합니다.
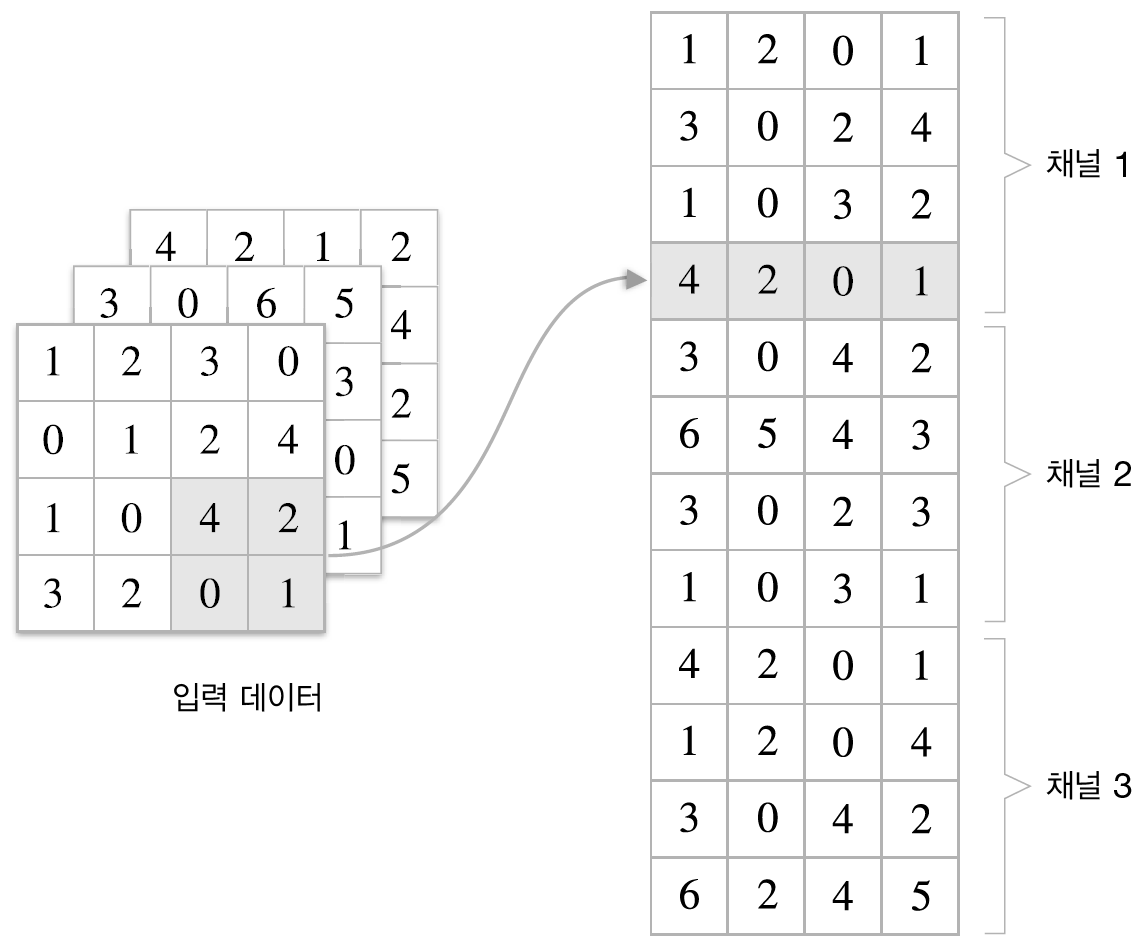
2차원 행렬에서 각 행의 최대값을 구하고 출력데이터의 크기 (N, C, OH, OW)에 맞게 변환합니다.
In [4]: class Pooling:
...: def __init__(self, pool_h, pool_w, stride=1, pad=0):
...: self.pool_h = pool_h
...: self.pool_w = pool_w
...: self.stride = stride
...: self.pad = pad
...:
...: self.x = None
...: self.arg_max = None
...:
...: def forward(self, x):
...: N, C, H, W = x.shape
...: out_h = int(1 + (H - self.pool_h) / self.stride)
...: out_w = int(1 + (W - self.pool_w) / self.stride)
...:
...: col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
...: col = col.reshape(-1, self.pool_h * self.pool_w)
...:
...: arg_max = np.argmax(col, axis=1)
...: out = np.max(col, axis=1)
...: out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
...:
...: self.x = x
...: self.arg_max = arg_max
...:
...: return out
...:
...: def backward(self, dout):
...: dout = dout.transpose(0, 2, 3, 1)
...:
...: pool_size = self.pool_h * self.pool_w
...: dmax = np.zeros((dout.size, pool_size))
...: dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
...: dmax = dmax.reshape(dout.shape + (pool_size,))
...:
...: dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
...: dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
...:
...: return dx
...:
순전파
im2col을 이용하여 4차원 데이터x를 2차원 데이터col = (N * OH * OW, C * PH * PW)로 변경합니다.col = col.reshape(-1, self.pool_h * self.pool_w)를 이용하여(N * OH * OW * C, PH * PW)크기로 변경합니다.out = np.max(col, axis=1)를 이용하여 각 행의 최대값을 구하여out배열에 저장합니다.reshape, transpose를 이용하여(N, C, OH, OW)크기로 변환하여 반환합니다.
역전파
dout은 순전파에서 출력되었던 형태인(N, C, OH, OW)크기로 입력됩니다.dout = dout.transpose(0, 2, 3, 1)를 통해서(N, OH, OW, C)크기로 변환합니다.dmax = np.zeros((dout.size, pool_size))에서 순전파 때 생성되었던col배열과 같은 크기인(N * OH * OW * C, PH * PW)크기의 영배열을 만듭니다.dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()를 이용하여 최대값을 가졌던 인덱스에 역전파된 미분값을 대입하고 나머지는0으로 놓습니다.dmax = dmax.reshape(dout.shape + (pool_size,))를 이용하여dmax의 크기를(N, OH, OW, C, PH * PW)크기로 변환합니다.dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)를 이용하여(N * OH * OW, C * PH * PW)형태로 변환합니다.dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)를 이용하여 순전파 때 입력되었던 원래 데이터의 크기self.x.shape로 변환하여 최대 풀링의 역전파를 반환합니다.
CNN 구현¶
다음은 단순한 합성곱 네트워크를 구현한 것입니다.
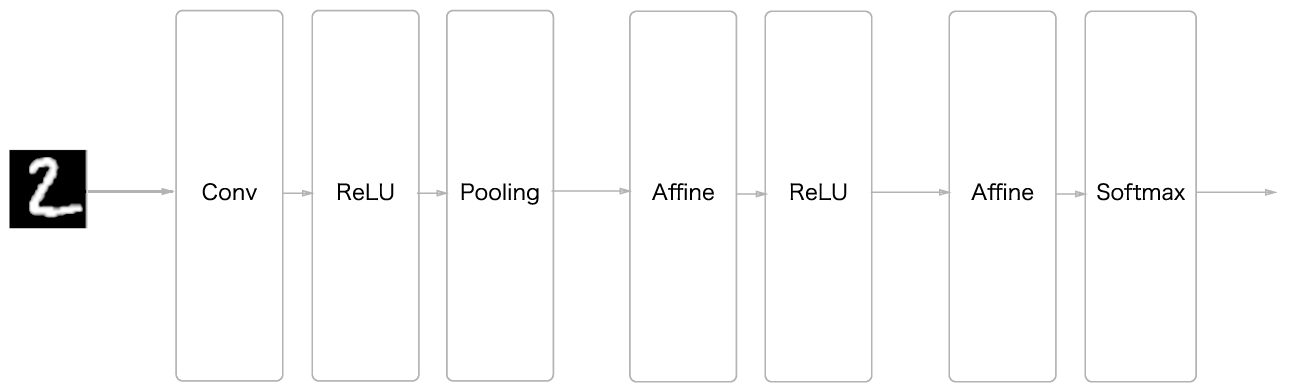
Conv -> Relu -> Pool(윈도우 크기는 2x2) -> Affine -> Relu -> Affine -> SoftmaxWithLoss
In [5]: import sys, os
...: sys.path.append(os.path.join(os.path.dirname(__file__), '..')) # 부모 디렉토리를 경로에 추가
...: import pickle
...: import numpy as np
...: from collections import OrderedDict
...: from common.layers import *
...: from common.gradient import numerical_gradient
...:
...:
...: class SimpleConvNet:
...: """단순한 ConvNet
...:
...: conv - relu - pool - affine - relu - affine - softmax
...:
...: Parameters
...: ----------
...: input_dim : 입력 크기(MNIST의 경우는 [1, 28, 28])
...: hidden_size : 은닉층 뉴런의 개수(e.g. 100)
...: output_size : 출력 사이즈(MNIST의 경우는 10)
...: activation : 'relu' or 'sigmoid'
...: weight_init_std : 가중치의 표준편차를 지정(e.g. 0.01)
...: 'relu' 또는 'he'를 지정했을 경우는 'He의 초기치'를 설정
...: 'sigmoid' 또는 'xavier'를 지정한 경우 'Xavier 초기치'를 설정
...: """
...:
...: def __init__(self, input_dim=(1, 28, 28),
...: conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
...: hidden_size=100, output_size=10, weight_init_std=0.01):
...: filter_num = conv_param['filter_num']
...: filter_size = conv_param['filter_size']
...: filter_pad = conv_param['pad']
...: filter_stride = conv_param['stride']
...: input_size = input_dim[1]
...: # 합성곱 계층의 출력데이터 크기
...: conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
...: # 풀링 계층의 출력데이터 크기; 풀링 필터의 크기는 2x2; 완전 연결로 연결됨.
...: pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
...:
...: # 가중치 초기화
...: self.params = {}
...: # 합성곱 계층 매개변수(필터: (FN, C, FH, FW))
...: self.params['W1'] = weight_init_std * \
...: np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
...: self.params['b1'] = np.zeros(filter_num)
...: # 첫번째 어파인 매개변수
...: self.params['W2'] = weight_init_std * \
...: np.random.randn(pool_output_size, hidden_size)
...: self.params['b2'] = np.zeros(hidden_size)
...: # 두번째 어파인 매개변수
...: self.params['W3'] = weight_init_std * \
...: np.random.randn(hidden_size, output_size)
...: self.params['b3'] = np.zeros(output_size)
...:
...: # 레이어 생성
...: self.layers = OrderedDict()
...: self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
...: conv_param['stride'], conv_param['pad'])
...: self.layers['Relu1'] = Relu()
...: self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
...: self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
...: self.layers['Relu2'] = Relu()
...: self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
...:
...: self.last_layer = SoftmaxWithLoss()
...:
...: def predict(self, x):
...: for layer in self.layers.values():
...: x = layer.forward(x)
...:
...: return x
...:
...: def loss(self, x, t):
...: """손실 함수
...: x는 입력데이터, t는 레이블
...: """
...: y = self.predict(x)
...: return self.last_layer.forward(y, t)
...:
...: def accuracy(self, x, t, batch_size=100):
...: if t.ndim != 1 : t = np.argmax(t, axis=1)
...:
...: acc = 0.0
...:
...: for i in range(int(x.shape[0] / batch_size)):
...: tx = x[i*batch_size:(i+1)*batch_size]
...: tt = t[i*batch_size:(i+1)*batch_size]
...: y = self.predict(tx)
...: y = np.argmax(y, axis=1)
...: acc += np.sum(y == tt)
...:
...: return acc / x.shape[0]
...:
...: def numerical_gradient(self, x, t):
...: """그래디언트(수치미분)
...:
...: Parameters
...: ----------
...: x : 입력데이터
...: t : 레이블
...:
...: Returns
...: -------
...: 각 층의 그래디언트를 가진 딕셔너리 변수
...: grads['W1']、grads['W2']、... 각층의 가중치
...: grads['b1']、grads['b2']、... 편향
...: """
...: loss_w = lambda w: self.loss(x, t)
...:
...: grads = {}
...: for idx in (1, 2, 3):
...: grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])
...: grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])
...:
...: return grads
...:
...: def gradient(self, x, t):
...: """그래디언트(오차역전파)
...:
...: Parameters
...: ----------
...: x : 입력데이터
...: t : 레이블
...:
...: Returns
...: -------
...: 각 층의 그래디언트를 가진 딕셔너리 변수
...: grads['W1']、grads['W2']、...각층의 가중치
...: grads['b1']、grads['b2']、...편향
...: """
...: # forward
...: self.loss(x, t)
...:
...: # backward
...: dout = 1
...: dout = self.last_layer.backward(dout)
...:
...: layers = list(self.layers.values())
...: layers.reverse()
...: for layer in layers:
...: dout = layer.backward(dout)
...:
...: # 설정
...: grads = {}
...: grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
...: grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
...: grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
...:
...: return grads
...:
...: def save_params(self, file_name="params.pkl"):
...: """매개변수 파일로 저장
...: """
...: params = {}
...: for key, val in self.params.items():
...: params[key] = val
...:
...: # 매개변수 피클 파일로 저장
...: with open(file_name, 'wb') as f:
...: pickle.dump(params, f)
...:
...: def load_params(self, file_name="params.pkl"):
...: """파일로부터 매개변수 설정
...: """
...: with open(file_name, 'rb') as f:
...: params = pickle.load(f)
...:
...: # 매개변수 설정
...: for key, val in params.items():
...: self.params[key] = val
...:
...: # 레이어 설정
...: for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
...: self.layers[key].W = self.params['W' + str(i+1)]
...: self.layers[key].b = self.params['b' + str(i+1)]
...:
가중치 매개변수는 Conv1, Affine1, Affine2 계층에 각각 부여됩니다.
Conv1¶
입력데이터 MNIST (1, 28, 28) 크기가 입력되고 출력은 필터의 갯수 FN와 필터의 크기 (FH, FW)에 의해 결정됩니다. 출력의 크기는 (N, FN, OH, OW) 입니다. 합성곱의 매개변수 W1는 필터의 크기에 의해 결정되므로 (FN, C, FH, FW) 가 됩니다. 편향은 (FN,) 이 됩니다.
Relu1¶
입력데이터는 앞 층의 합성곱 계층의 출력데이터 (N, FN, OH, OW) 이고 Relu1의 출력 크기도 마찬가지로 변하지 않습니다.
Pooling¶
풀링의 입력은 앞 층의 Relu1의 크기인 (N, FN, OH, OW) 이고 출력데이터의 크기는 (N, FN, OH, OW) 입니다. 그런데 다음 계층이 완전 연결 계층인 어파인 이므로 어파인에 연결될 때는 (N, FN * OH * OW)가 됩니다.
Affine1¶
풀링 출력데이터가 4차원 데이터인데 어파인에 입력되어 2차원으로 바뀌어 처리가 됩니다. 즉, (N, FN * OH * OW)로 처리됩니다. 따라서 어파인의 매개변수 W2의 크기는 (FN * OH * OW, 은닉 노드의 갯수) 가 됩니다. 어파인의 편향은 (은닉 노드의 갯수,)가 됩니다. Affine1의 출력데이터 크기는 (N, 은닉 노드의 갯수)가 됩니다.
Relu2¶
Relu1과 마찬가지로 입력데이터의 크기만큼 출력데이터로 나옵니다. 입/출력데이터의 크기는 (N, 은닉 노드의 갯수)가 됩니다.
Affine2¶
Affine2의 출력은 최종 출력층이 되므로 매개변수 W3의 MNIST의 분류 갯수인 10이 되므로 앞 층의 입력데이터의 크기와 함께 (은닉 노드의 갯수, 10)이 됩니다. 편향은 (10,) 이 됩니다.
SoftmaxWithLoss¶
출력층의 활성화함수 소프트맥스와 오차가 함께 처리되는 층입니다.
CNN 학습¶
SimpleConvNet을 이용해 MNIST 학습을 하는 코드입니다.
import sys, os
sys.path.append(os.path.join(os.path.dirname(__file__), '..')) # 부모 디렉토리를 경로에 추가
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from simple_convnet import SimpleConvNet
from common.trainer import Trainer
# 데이터읽기
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)
# 처리하는데 시간이 걸릴 경우 데이터 줄임
#x_train, t_train = x_train[:5000], t_train[:5000]
#x_test, t_test = x_test[:1000], t_test[:1000]
# 에폭 수
max_epochs = 20
network = SimpleConvNet(input_dim=(1,28,28),
conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=max_epochs, mini_batch_size=100,
optimizer='Adam', optimizer_param={'lr': 0.001},
evaluate_sample_num_per_epoch=1000)
trainer.train()
# 매개변수 저장
network.save_params("params.pkl")
print("Saved Network Parameters!")
# 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
다음은 학습자(Trainer) 클래스를 나타냅니다. Trainer 클래스는 주어진 신경망을 학습하는 과정이 들어 있습니다.
import sys, os
sys.path.append(os.path.join(os.path.dirname(__file__), '..')) # 부모 디렉토리를 경로에 추가
import numpy as np
from common.optimizer import *
class Trainer:
"""신경망 학습 클래스
"""
def __init__(self, network, x_train, t_train, x_test, t_test,
epochs=20, mini_batch_size=100,
optimizer='SGD', optimizer_param={'lr':0.01},
evaluate_sample_num_per_epoch=None, verbose=True):
self.network = network
self.verbose = verbose
self.x_train = x_train # 훈련데이터
self.t_train = t_train # 훈련데이터의 레이블
self.x_test = x_test # 테스트 데이터
self.t_test = t_test # 테스트 데이터의 레이블
self.epochs = epochs # 에폭의 갯수
self.batch_size = mini_batch_size # 데이터의 배치 크기
self.evaluate_sample_num_per_epoch = evaluate_sample_num_per_epoch
# optimizer
optimizer_class_dict = {'sgd':SGD, 'momentum':Momentum, 'nesterov':Nesterov,
'adagrad':AdaGrad, 'rmsprpo':RMSprop, 'adam':Adam}
self.optimizer = optimizer_class_dict[optimizer.lower()](**optimizer_param)
self.train_size = x_train.shape[0]
self.iter_per_epoch = max(self.train_size / mini_batch_size, 1)
self.max_iter = int(epochs * self.iter_per_epoch)
self.current_iter = 0
self.current_epoch = 0
self.train_loss_list = []
self.train_acc_list = []
self.test_acc_list = []
def train_step(self):
"""배치 단위 데이터 학습
"""
batch_mask = np.random.choice(self.train_size, self.batch_size)
x_batch = self.x_train[batch_mask]
t_batch = self.t_train[batch_mask]
# 그레디언트 계산
grads = self.network.gradient(x_batch, t_batch)
# 그레디언트 갱신
self.optimizer.update(self.network.params, grads)
loss = self.network.loss(x_batch, t_batch)
self.train_loss_list.append(loss)
if self.verbose: print("train loss:" + str(loss))
if self.current_iter % self.iter_per_epoch == 0:
self.current_epoch += 1
x_train_sample, t_train_sample = self.x_train, self.t_train
x_test_sample, t_test_sample = self.x_test, self.t_test
if not self.evaluate_sample_num_per_epoch is None:
t = self.evaluate_sample_num_per_epoch
x_train_sample, t_train_sample = self.x_train[:t], self.t_train[:t]
x_test_sample, t_test_sample = self.x_test[:t], self.t_test[:t]
train_acc = self.network.accuracy(x_train_sample, t_train_sample)
test_acc = self.network.accuracy(x_test_sample, t_test_sample)
self.train_acc_list.append(train_acc)
self.test_acc_list.append(test_acc)
if self.verbose: print("=== epoch:" + str(self.current_epoch) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc) + " ===")
self.current_iter += 1
def train(self):
"""신경망 학습
"""
for i in range(self.max_iter):
self.train_step()
test_acc = self.network.accuracy(self.x_test, self.t_test)
if self.verbose:
print("=============== Final Test Accuracy ===============")
print("test acc:" + str(test_acc))