넘파이(NumPy) 기초: 배열 및 벡터 계산

넘파이 ndarray: 다차원 배열 객체

넘파이(numpy)의 주요 특징 중의 하나가 n차원 배열(ndarray) 객체이다. 이 객체는 빠르고 유연한 자료형이다. 수학식에서 행렬 연산과 비슷한 연산을 할 수 있다. 즉, 성분별 계산을 할 수 있다. 다음 예를 보자.

import numpy as np

data = np.random.randn(2, 3)
data

array([[-1.25858421,  0.21625778,  1.48456228],
       [-1.5184562 ,  0.54263558, -0.62803821]])

data에 수학 연산을 다음과 같이 할 수 있다.

10 * data

array([[-12.58584208,   2.16257785,  14.84562276],
       [-15.18456198,   5.42635578,  -6.2803821 ]])

data + data

array([[-2.51716842,  0.43251557,  2.96912455],
       [-3.0369124 ,  1.08527116, -1.25607642]])

ndarray는 배열의 크기인 shape와 배열 원소들의 자료형 dtype 속성을 가지고 있다.

data.dtype

dtype('float64')

data.shape

(2, 3)

앞으로 넘파이 배열, 배열(array), ndarray는 모두 numpy.ndarray 객체를 의미한다.

ndarray 만들기

넘파이 배열을 만드는 가장 쉬운 방법은 numpy.array 메소드를 이용하는 것이다. array 메소드는 반복 가능 객체를 인자로 받을 수 있으므로 다음과 같이 리스트를 배열로 만들 수 있다.

data1 = [1, 2, 3.5, 4, 5]

arr = np.array(data1)
arr

array([1. , 2. , 3.5, 4. , 5. ])

중첩된 리스트도 다차원 배열로 변환할 수 있다.

data2 = [[1, 2, 3, 4], [5, 6, 7, 8]]

arr2 = np.array(data2)
arr2

array([[1, 2, 3, 4],
       [5, 6, 7, 8]])

변경된 배열의 차원은 ndim을 이용해서 알 수 있다.

arr2.ndim

2

arr2.shape

(2, 4)

배열의 형도 원소들에 따라 자동으로 설정된다.

arr2.dtype

dtype('int32')

그밖에도 많은 방법으로 배열을 생성할 수 있지만 zeros와 ones를 이용해서 0및 1로 이루어진 배열을 만들 수 있다.

np.zeros(10)

array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

2 x 3 크기의 배열을 만들 때 (2, 3)과 같이 인자로 튜플을 건네주어야 한다.

np.ones((2, 3))

array([[1., 1., 1.],
       [1., 1., 1.]])

arange 함수는 파이썬의 range 함수에 대응되는 것이지만 반환값은 넘파이 배열이다.

np.arange(10)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

다음은 넘파이 배열을 만드는 함수들이다.

함수	설명
array	Convert input data (list, tuple, array, or other sequence type) to an ndarray either by inferring a dtype or explicitly specifying a dtype; copies the input data by default
asarray	Convert input to ndarray, but do not copy if the input is already an ndarray
arange	Like the built-in range but returns an ndarray instead of a list
ones, ones_like	Produce an array of all 1s with the given shape and dtype; ones_like takes another array and produces a ones array of the same shape and dtype
zeros, zeros_like	Like ones and ones_like but producing arrays of 0s instead
empty, empty_like	Create new arrays by allocating new memory, but do not populate with any values like ones and zeros
full, full_like	Produce an array of the given shape and dtype with all values set to the indicated “fill value” full_like takes another array and produces a filled array of the same shape and dtype
eye, identity	Create a square N × N identity matrix (1s on the diagonal and 0s elsewhere)|

넘파이 자료형

자료형(data type) 또는 dtype는 메모리 구역을 넘파이 배열이 의미있는 정보로 해석할 수 있는 객체이다.

arr1 = np.array([1, 2, 3], dtype=np.float64)
arr2 = np.array([1, 2, 3], dtype=np.int64)

arr1.dtype

dtype('float64')

arr2.dtype

dtype('int64')

아래 표는 넘파이 자료형이다.

Type	Type code	Description
int8, uint8	i1, u1	부호가 있는, 부호가 없는 8비트(1바이트) 정수형
int16, uint16	i2, u2	부호가 있는, 부호가 없는 16비트(2바이트) 정수형
int32, uint32	i4, u4	부호가 있는, 부호가 없는 32비트(4바이트) 정수형
int64, uint64	i8, u8	부호가 있는, 부호가 없는 64비트(8바이트) 정수형
float16	f2	16비트 부동소수점형
float32	f4 or f	표준 단정밀도(32비트) 부동소수점형; C 부동소수점형과 호환
float64	f8 or d	표준 배정밀도(64비트) 부동소수점형; C 배정밀도, 파이썬 부동소수점형
float12 8	f16 or g	확장 정밀도 부동소수점형
complex 64, complex 128, complex 256	c8, c16, c32	2개의 32, 64, 128 비트 복소수 부동소수점형
bool	?	참(True), 거짓(False)를 저장하는 논리형
object	O	파이썬 객체 타입; 어떤 파이썬 객체도 가능
string_	S	고정 길이 아스키 문자열 형(한 문자당 1바이트); 예를 들어, 길이 10인 문자열 생성을 위해서 ‘S10’ 사용
unicode _	U	고정 길이 유니코드 문자열 형(한 문자당 사용되는 바이트는 인코딩에 따라 다르다.); 예를 들어, 길이 10인 문자열 생성을 위해서 ‘U10’ 사용

astype 메소드를 이용해서 다른 형으로 전환할 수 있다.

arr = np.array([1, 2, 3, 4, 5])
arr.dtype

dtype('int32')

다음은 정수형 32비트를 부동소수점형 64비트로 전환한다.

arr_float = arr.astype(np.float64)
arr_float.dtype

dtype('float64')

반대로 부동소수점형을 정수형으로 변경하면 다음과 같이 소수점 아래 수들이 사라진다.

arr = np.array([1.2, 3.4, -0.9, -2.1, 100.])
arr_int = arr.astype(np.int32)
arr_int

array([  1,   3,   0,  -2, 100])

숫자 문자열로 주어진 배열도 숫자형으로 변경할 수 있다.

num_str = np.array(['1.234', '-2.29', '1000'], dtype=np.string_)
num_str

array([b'1.234', b'-2.29', b'1000'], dtype='|S5')

num = num_str.astype(np.float)
num.dtype

dtype('float64')

다른 배열의 자료형 속성을 이용해서 자료형을 변경할 수도 있다.

arr_int = np.arange(10)
caliber = np.array([.22, 0.33, 2.1], dtype='f8')
caliber.dtype

dtype('float64')

arr_int.astype(caliber.dtype)

array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

넘파이 배열 연산

넘파일 배열간의 연산은 반복문을 사용하지 않고서도 내부적으로 연산을 할 수 있다. 기본적으로 성분끼리 연산을 하는데 이러한 연산을 벡터화 계산(vectorization)이라고 한다.

arr = np.array([[1., 2., 3.], [4., 5., 6.]])
arr

array([[1., 2., 3.],
       [4., 5., 6.]])

arr * arr

array([[ 1.,  4.,  9.],
       [16., 25., 36.]])

arr - arr

array([[0., 0., 0.],
       [0., 0., 0.]])

1 / arr

array([[1.        , 0.5       , 0.33333333],
       [0.25      , 0.2       , 0.16666667]])

두 배열간의 비교 연산도 가능하다.

arr2 = np.array([[0., 4., 1.], [7., 2., 12.]])
arr2

array([[ 0.,  4.,  1.],
       [ 7.,  2., 12.]])

arr < arr2

array([[False,  True, False],
       [ True, False,  True]])

크기가 다른 배열간에도 연산이 가능하다. 이러한 연산을 브로드캐스팅(broadcasting)이라고 한다.

인덱싱, 슬라이싱 기본

넘파이 인덱싱은 많은 설명이 필요 하지만 1차원 배열은 간단하다.

arr = np.arange(10)
arr

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

arr[5]

5

arr[5:8]

array([5, 6, 7])

arr[5:8] = 10
arr

array([ 0,  1,  2,  3,  4, 10, 10, 10,  8,  9])

파이썬 리스트와 크게 다른점중의 하나는 배열 슬라이스는 새로운 객체를 만드는 것이 아닌 원래 배열에 대한 뷰(view)이다. 즉 선택 부분의 값을 변경하면 원래 배열의 같은 위치의 값도 변경이 되는 것이다.

arr_slice = arr[5:8]
arr_slice

array([10, 10, 10])

다음과 같이 arr_slice의 부분을 변경하면 원래 배열 arr도 값이 변경된 것을 알 수 있다.

arr_slice[1] = 1234
arr

array([   0,    1,    2,    3,    4,   10, 1234,   10,    8,    9])

시작과 끝이 없는 슬라이싱은 모든 원소를 선택하는 것이기 때문에 다음은 모든 값을 변경하게 된다.

arr_slice[:] = 500
arr

array([  0,   1,   2,   3,   4, 500, 500, 500,   8,   9])

배열의 일부분을 복사해서 사용하려면 copy 메소드를 이용할 수 있다.

arr_copy = arr[5:8].copy()
arr_copy

array([500, 500, 500])

arr_copy[:] = -100
arr_copy

array([-100, -100, -100])

arr_copy 값이 변경되었지만 arr 값은 변경되지 않은 것을 확인할 수 있다.

arr

array([  0,   1,   2,   3,   4, 500, 500, 500,   8,   9])

고차원 배열은 생각해야 할 것이 많아진다. 2차원 배열을 생각해보자. 각 인덱스에 해당하는 원소는 스칼라가 아니고 1차원 벡터가 된다.

arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
arr2d[0]

array([1, 2, 3])

개개의 원소들은 대괄호를 반복적으로 사용하여 접근할 수도 있고 쉼표를 이용하여 접근할 수도 있다.

arr2d[0][1]

2

arr2d[0, 1]

2

2차원 배열 인덱스에서 첫번째 성분은 행, 두번째 성분은 열을 의미한다고 볼 수 있다. 다차원 배열에서 뒤쪽 인덱스를 생략하면 저차원 배열을 반환한다. 가령 2 x 2 x 3 배열:

arr3d = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
arr3d

array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

arr3d[0]는 2 x 3 배열이 된다.

arr3d[0]

array([[1, 2, 3],
       [4, 5, 6]])

arr3d[0, 1]은 1 x 3 배열이 된다.

arr3d[0, 1]

array([4, 5, 6])

arr3d[0]에 스칼라 또는 벡터가 할당될 수 있다.

old = arr3d[0].copy()

arr3d[0] = 100
arr3d

array([[[100, 100, 100],
        [100, 100, 100]],

       [[  7,   8,   9],
        [ 10,  11,  12]]])

다음과 같이 인덱스 arr3d[0, 1]를 2단계로 나눠서 할 수 있다.

arr3d[0] = old

x = arr3d[0]
x

array([[1, 2, 3],
       [4, 5, 6]])

x[1]

array([4, 5, 6])

슬라이싱을 이용한 인덱싱

파이썬 리스트에 사용했던 슬라이싱을 넘파이 배열에서도 마찬가지로 사용할 수 있다. 다음과 같은 2차원 배열을 생각해보자.

arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
arr2d

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

arr2d[:2]

array([[1, 2, 3],
       [4, 5, 6]])

위에서 보는 바와 같이 0번째, 1번째 1차원배열을 합친 2차원 배열을 반환하는 것을 알 수 있다. 인덱스를 성분별로 지정했듯이 슬라이싱도 성분별로 지정할 수 있다.

arr2d[:2, 1:]

array([[2, 3],
       [5, 6]])

두번째행 두번째, 세번째열을 선택하려면 다음과 같이 할 수 있다.

arr2d[1, 1:]

array([5, 6])

마찬가지로 3번째 열, 첫번째, 두번째 행을 선택은 다음과 같다.

arr2d[:2, 2]

array([3, 6])

콜론은 모든 인덱스를 의미하므로 다음은 첫번째 열을 선택한다.

arr2d[:, :1]

array([[1],
       [4],
       [7]])

앞에서와 마찬가지로 선택된 부분에 값을 대입하면 모든 값이 변경된다.

arr2d[:2, 1:] = 0
arr2d

array([[1, 0, 0],
       [4, 0, 0],
       [7, 8, 9]])

논리 인덱싱

중복된 이름 배열과 이름에 대응되는 숫자들 자료가 있다고 하자.

names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])

np.random.seed(0)

data = np.random.randn(7, 4)
data

array([[ 1.76405235,  0.40015721,  0.97873798,  2.2408932 ],
       [ 1.86755799, -0.97727788,  0.95008842, -0.15135721],
       [-0.10321885,  0.4105985 ,  0.14404357,  1.45427351],
       [ 0.76103773,  0.12167502,  0.44386323,  0.33367433],
       [ 1.49407907, -0.20515826,  0.3130677 , -0.85409574],
       [-2.55298982,  0.6536186 ,  0.8644362 , -0.74216502],
       [ 2.26975462, -1.45436567,  0.04575852, -0.18718385]])

Bob에 해당하는 숫자들의 행만 선택하기를 원한다. 비교 연산자 ==를 이용하면 벡터화된 논리 배열을 얻을 수 있다.

names == 'Bob'

array([ True, False, False,  True, False, False, False])

이 논리배열은 다른 배열의 인덱스로 사용될 수 있다. 인덱스로 사용될 논리 배열의 크기와 인덱스를 사용할 배열의 크기가 같아야 한다.

data[names == "Bob"]

array([[1.76405235, 0.40015721, 0.97873798, 2.2408932 ],
       [0.76103773, 0.12167502, 0.44386323, 0.33367433]])

다음과 같이 다중 인덱스를 사용할 수 있다.

data[names == 'Bob', 2:]

array([[0.97873798, 2.2408932 ],
       [0.44386323, 0.33367433]])

Bob을 제외한 모든 자료를 선택하려면 !=를 사용하면 된다.

data[names != 'Bob']

array([[ 1.86755799, -0.97727788,  0.95008842, -0.15135721],
       [-0.10321885,  0.4105985 ,  0.14404357,  1.45427351],
       [ 1.49407907, -0.20515826,  0.3130677 , -0.85409574],
       [-2.55298982,  0.6536186 ,  0.8644362 , -0.74216502],
       [ 2.26975462, -1.45436567,  0.04575852, -0.18718385]])

또는 부정 연산자 ~를 사용해도 된다.

data[~(names == 'Bob')]

array([[ 1.86755799, -0.97727788,  0.95008842, -0.15135721],
       [-0.10321885,  0.4105985 ,  0.14404357,  1.45427351],
       [ 1.49407907, -0.20515826,  0.3130677 , -0.85409574],
       [-2.55298982,  0.6536186 ,  0.8644362 , -0.74216502],
       [ 2.26975462, -1.45436567,  0.04575852, -0.18718385]])

여러 개의 조건을 결합하려면 &(and) 또는 |(or) 연산자를 사용하면 된다. 주의해야 할 것은 넘파이 논리 연산자로 파이썬 논리 연산자 and와 or를 사용할 수 없다. 반드시 &와 |만 사용해야 한다.

mask = (names == 'Bob') | (names == 'Will')
mask

array([ True, False,  True,  True,  True, False, False])

arr_m = data[mask]
arr_m

array([[ 1.76405235,  0.40015721,  0.97873798,  2.2408932 ],
       [-0.10321885,  0.4105985 ,  0.14404357,  1.45427351],
       [ 0.76103773,  0.12167502,  0.44386323,  0.33367433],
       [ 1.49407907, -0.20515826,  0.3130677 , -0.85409574]])

또한 논리 인덱스를 이용해서 반환된 배열을 원래 배열의 복사본이기때문에 반환된 배열값이 바뀌어도 원본값은 변하지 않는다.

arr_m[:, :2] = 0
arr_m

array([[ 0.        ,  0.        ,  0.97873798,  2.2408932 ],
       [ 0.        ,  0.        ,  0.14404357,  1.45427351],
       [ 0.        ,  0.        ,  0.44386323,  0.33367433],
       [ 0.        ,  0.        ,  0.3130677 , -0.85409574]])

data

array([[ 1.76405235,  0.40015721,  0.97873798,  2.2408932 ],
       [ 1.86755799, -0.97727788,  0.95008842, -0.15135721],
       [-0.10321885,  0.4105985 ,  0.14404357,  1.45427351],
       [ 0.76103773,  0.12167502,  0.44386323,  0.33367433],
       [ 1.49407907, -0.20515826,  0.3130677 , -0.85409574],
       [-2.55298982,  0.6536186 ,  0.8644362 , -0.74216502],
       [ 2.26975462, -1.45436567,  0.04575852, -0.18718385]])

논리 배열 인덱스를 통해서 원래 배열의 값을 변경하는 것은 상식적이다. 0보다 작은 수를 0으로 바꾸는 것은 다음과 같다.

data[data < 0] = 0
data

array([[1.76405235, 0.40015721, 0.97873798, 2.2408932 ],
       [1.86755799, 0.        , 0.95008842, 0.        ],
       [0.        , 0.4105985 , 0.14404357, 1.45427351],
       [0.76103773, 0.12167502, 0.44386323, 0.33367433],
       [1.49407907, 0.        , 0.3130677 , 0.        ],
       [0.        , 0.6536186 , 0.8644362 , 0.        ],
       [2.26975462, 0.        , 0.04575852, 0.        ]])

이름이 Joe가 아닌 행의 값을 7로 변경하는 것은 다음과 같다.

data[names != 'Joe'] = 7
data

array([[7.        , 7.        , 7.        , 7.        ],
       [1.86755799, 0.        , 0.95008842, 0.        ],
       [7.        , 7.        , 7.        , 7.        ],
       [7.        , 7.        , 7.        , 7.        ],
       [7.        , 7.        , 7.        , 7.        ],
       [0.        , 0.6536186 , 0.8644362 , 0.        ],
       [2.26975462, 0.        , 0.04575852, 0.        ]])

정수 배열을 이용한 인덱싱

정수 배열을 이용해서 인덱싱을 자유롭게 할 수 있다. 예를 위해 다음과 같은 배열을 만들어 보자.

arr = np.empty((8, 4))

for i in range(8):
    arr[i] = i
arr

array([[0., 0., 0., 0.],
       [1., 1., 1., 1.],
       [2., 2., 2., 2.],
       [3., 3., 3., 3.],
       [4., 4., 4., 4.],
       [5., 5., 5., 5.],
       [6., 6., 6., 6.],
       [7., 7., 7., 7.]])

원하는 행을 뽑아서 원하는 순서로 배열하고 싶으면 행에 해당하는 인덱스를 배열로 만들어 대입하면 된다.

arr[[4, 3, 0, 6]]

array([[4., 4., 4., 4.],
       [3., 3., 3., 3.],
       [0., 0., 0., 0.],
       [6., 6., 6., 6.]])

음수 인덱스도 가능하다.

arr[[-4, -5, 0, 6]]

array([[4., 4., 4., 4.],
       [3., 3., 3., 3.],
       [0., 0., 0., 0.],
       [6., 6., 6., 6.]])

여러 개의 정수 배열 인덱싱은 약간 다르다. 다중 정수 배열 인덱싱 결과는 항상 1차원 배열이다.

arr = np.arange(32).reshape(8, 4)
arr

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19],
       [20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])

다음과 같이 정수열 배열 인덱스를 2개의 성분에 대입하면 결과값은 각각의 튜플에 해당하는 일차원 배열이 나온다.

arr[[1, 5, 7, 2], [0, 3, 1, 2]]

array([ 4, 23, 29, 10])

즉, 인덱스 (1, 0), (5, 3), (7, 1), (2, 2) 원소들이 일차원 배열로 반환된다. 언뜻 보기에는 1, 5, 7, 2행 인덱스와 0, 3, 1, 2열 인덱스에 해당하는 직사각형 배열을 생각할 수 있지만 그렇지 않은 것을 알 수 있다. 이러한 배열은 다음과 같이 만들 수 있다.

arr[[1, 5, 7, 2]][:, [0, 3, 1, 2]]

array([[ 4,  7,  5,  6],
       [20, 23, 21, 22],
       [28, 31, 29, 30],
       [ 8, 11,  9, 10]])

주의해야할 것은 정수 배열 인덱싱해서 나온 배열은 원래 배열의 복사본이다.

배열 전치 및 축 교환

전치(transpose)는 크기변경(reshape)의 특별한 형태이다. 배열은 transpose 메소드를 가지며 T 속성도 가지고 있다.

import numpy as np

arr = np.arange(15).reshape((3, 5))
arr

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

배열의 T 속성을 이용하면 transpose를 할 수 있다.

arr.T

array([[ 0,  5, 10],
       [ 1,  6, 11],
       [ 2,  7, 12],
       [ 3,  8, 13],
       [ 4,  9, 14]])

행렬 계산을 할 때 전치 행렬을 자주 사용하게 된다. 예를 들어 두 행렬의 곱을 계산할 때 dot 메소드를 이용하는데 다음과 같이 계산할 수 있다.

arr.dot(arr.T)

array([[ 30,  80, 130],
       [ 80, 255, 430],
       [130, 430, 730]])

고차원 배열에서 transpose는 축 인덱스를 인자로 갖는다. 다음과 같이 2 x 3 x 4 3차원 배열 arr3d를 생각해보자.

arr3d = np.arange(2 * 3 * 4).reshape((2, 3, 4))
arr3d

array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])

다음은 두번째 축을 첫번째로, 첫번째 축은 두번째로 옮긴 예이다.

arr3d.transpose((1, 0 , 2))

array([[[ 0,  1,  2,  3],
        [12, 13, 14, 15]],

       [[ 4,  5,  6,  7],
        [16, 17, 18, 19]],

       [[ 8,  9, 10, 11],
        [20, 21, 22, 23]]])

위에서 두번째 축 성분을 고정시킨뒤 첫번째 축을 고정시키고 마지막 세번째 축 성분을 모두 나열하여 새로운 배열의 (0, 0) 성분 [0, 1, 2 3]을 만들고, 다음은 두번째 축은 고정시킨채 첫번째 축 성분을 이동하고 다음은 세번째 축 성분을 모두 나열하여 (0, 1) 성분 [12, 13, 14, 15]을 만든다. 두번째 성분을 하나 이동하여 [4, 5, 6, 7] 성분 (1, 0)을 찾고, 다음은 두번째 성분은 고정시킨채 첫번째 성분을 이동하여 [16, 17, 18, 19] 성분 (1, 1)을 만든다. 마지막으로 두번째 성분을 한번 더 이동하여 [8, 9, 10, 11] 성분 (2, 0)을 만들고, 첫번째 성분을 이동시켜 [20, 21, 22, 23] 성분 (2, 1)을 만든다. 최종적으로 3 x 2 x 4 배열이 만들어 진다.

고차원 배열에서 T와 인자없는 transpose() 메소드는 원래 배열의 축의 순서를 거꾸로 출력한다.

직접하기

• 위의 arr3d 배열에 대해서 arr3d.transpose(2, 0, 1)의 값을 손으로 구하고 메소드로 구한 것과 비교하시오.

arr3d.T

array([[[ 0, 12],
        [ 4, 16],
        [ 8, 20]],

       [[ 1, 13],
        [ 5, 17],
        [ 9, 21]],

       [[ 2, 14],
        [ 6, 18],
        [10, 22]],

       [[ 3, 15],
        [ 7, 19],
        [11, 23]]])

swapaxes(i, j)는 i 축과 j축만 바꾸는 것이다. 따라서 arr3d.swapaxes(0, 2)는 arr3d.transpose(2, 1, 0)과 같다.

arr3d.swapaxes(2, 0)

array([[[ 0, 12],
        [ 4, 16],
        [ 8, 20]],

       [[ 1, 13],
        [ 5, 17],
        [ 9, 21]],

       [[ 2, 14],
        [ 6, 18],
        [10, 22]],

       [[ 3, 15],
        [ 7, 19],
        [11, 23]]])

범용함수

범용함수(universal function or ufunc)이란 넘파이 배열의 성분끼리 연산을 할 수 있는 함수를 말한다. sqrt, exp와 같은 함수들이 성분별 연산을 한다.

arr = np.arange(10)
arr

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

np.sqrt(arr)

array([0.        , 1.        , 1.41421356, 1.73205081, 2.        ,
       2.23606798, 2.44948974, 2.64575131, 2.82842712, 3.        ])

np.exp(arr)

array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
       5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
       2.98095799e+03, 8.10308393e+03])

위와 같이 인자를 하나만 갖는 함수를 단항 함수(unary function)이라고 한다. add, maximum 함수들은 두 개의 인자를 갖는다.

np.add(arr, arr)

array([ 0,  2,  4,  6,  8, 10, 12, 14, 16, 18])

rng = np.random.RandomState(0)

x = rng.randn(10)
y = rng.randn(10)
x

array([ 1.76405235,  0.40015721,  0.97873798,  2.2408932 ,  1.86755799,
       -0.97727788,  0.95008842, -0.15135721, -0.10321885,  0.4105985 ])

y

array([ 0.14404357,  1.45427351,  0.76103773,  0.12167502,  0.44386323,
        0.33367433,  1.49407907, -0.20515826,  0.3130677 , -0.85409574])

maximum 함수는 두 배열의 같은 위치의 성분중 큰 값을 반환한다.

np.maximum(x, y)

array([ 1.76405235,  1.45427351,  0.97873798,  2.2408932 ,  1.86755799,
        0.33367433,  1.49407907, -0.15135721,  0.3130677 ,  0.4105985 ])

arr = rng.randn(7) * 5
arr

array([-0.93591925,  7.66389607,  7.34679385,  0.77473713,  1.8908126 ,
       -4.43892874, -9.90398234])

흔하지는 않지만 범용함수 중 여러 개의 값을 반환하는 것도 있다. 파이썬 내장함수 divmod와 같은 역할을 하는 modf라는 함수는 정수와 소수부분을 각각 반환한다.

rem_part, int_part = np.modf(arr)
rem_part

array([-0.93591925,  0.66389607,  0.34679385,  0.77473713,  0.8908126 ,
       -0.43892874, -0.90398234])

int_part

array([-0.,  7.,  7.,  0.,  1., -4., -9.])

범용함수는 선택 인자 out=을 이용해서 결과값이 저장되는 공간을 자신으로 지정할 수 있다.

np.sqrt(arr, out=arr)

C:\Users\dyoon\Anaconda3\lib\site-packages\ipykernel_launcher.py:1: RuntimeWarning: invalid value encountered in sqrt
  """Entry point for launching an IPython kernel.

array([       nan, 2.76837427, 2.71049697, 0.88019153, 1.37506822,
              nan,        nan])

arr

array([       nan, 2.76837427, 2.71049697, 0.88019153, 1.37506822,
              nan,        nan])

다음은 단항함수들이다.

Function	Description
abs, fabs	정수, 부동소수점, 복소수형의 절대값 계산
sqrt	제곱근 계산(arr ** 0.5과 동일)
square	제곱 계산(arr ** 2과 동일)
exp	\(e^x\) 계산
log, log10, log2, log1p	각각 자연로그(밑이 e), 밑이 10인 로그, 밑이 2인 로그, 및 log(1 + x) 계산
sign	각 성분의 부호 계산: 1 (양수), 0 (영), 또는 -1 (음수)
ceil	성분보다 크거나 같은 정수 중 가장 작은 정수(천장함수)
floor	성분보다 작거나 같은 정수 중 가장 큰 정수(바닥함수)
rint	Round elements to the nearest integer, preserving the dtype
modf	Return fractional and integral parts of array as a separate array
isnan	Return boolean array indicating whether each value is NaN (Not a Number)
isfinite, isinf	Return boolean array indicating whether each element is finite (non-inf, non-NaN) or infinite, respectively
cos, cosh, sin, sinh, tan, tanh	삼각함수 및 쌍곡 삼각함수들
arccos, arccosh, arcsin, arcsinh, arctan, arctanh	역 삼각함수들
logical_ not	Compute truth value of not x element-wise (equivalent to ~arr).

다음은 이항 함수들이다.

Function	Description
add	Add corresponding elements in arrays
subtract	Subtract elements in second array from first array
multiply	Multiply array elements
divide, floor_d ivide	Divide or floor divide (truncating the remainder)
power	Raise elements in first array to powers indicated in second array
maximum, fmax	Element-wise maximum; fmax ignores NaN
minimum, fmin	Element-wise minimum; fmin ignores NaN
mod	Element-wise modulus (remainder of division)
copysign	Copy sign of values in second argument to values in first argument
greater, greater_equal, less, less_eq ual, equal, not_equ al	Perform element-wise comparison, yielding boolean array (equivalent to infix operators >, >=, <, <=, ==, !=)
logical_and, logical_or, logical_xor	Compute element-wise truth value of logical operation (equivalent to infix operators & |, ^)

배열 지향 프로그래밍

1차원 자료를 이용해 이차원 계산을 쉽게 할 수 있다. meshgrid 함수를 이용하면 모든 격자점의 x, y 좌표를 계산할 수 있다.

points = np.arange(-5, 5, 0.01)

meshgrid를 이용해서 -5부터 5까지 1000개의 점을 격자형으로 만든다.

xs, ys = np.meshgrid(points, points)
ys

array([[-5.  , -5.  , -5.  , ..., -5.  , -5.  , -5.  ],
       [-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
       [-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
       ...,
       [ 4.97,  4.97,  4.97, ...,  4.97,  4.97,  4.97],
       [ 4.98,  4.98,  4.98, ...,  4.98,  4.98,  4.98],
       [ 4.99,  4.99,  4.99, ...,  4.99,  4.99,  4.99]])

함수의 값 계산은 각 점에서 스칼라 계산을 한다.

z = np.sqrt(xs ** 2 + ys ** 2)
z

array([[7.07106781, 7.06400028, 7.05693985, ..., 7.04988652, 7.05693985,
        7.06400028],
       [7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
        7.05692568],
       [7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
        7.04985815],
       ...,
       [7.04988652, 7.04279774, 7.03571603, ..., 7.0286414 , 7.03571603,
        7.04279774],
       [7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
        7.04985815],
       [7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
        7.05692568]])

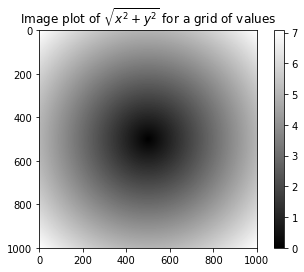
자료 시각화 장에서 배우게 될 matplotlib를 이용해서 계산된 값을 시각화해보자.

%matplotlib inline
import matplotlib.pyplot as plt

plt.imshow(z, cmap=plt.cm.gray)
plt.colorbar()
plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")

Text(0.5,1,'Image plot of $\\sqrt{x^2 + y^2}$ for a grid of values')

조건 연산을 이용한 배열 계산

numpy.where는 파이썬 삼항연산 <참일 때 식> if <참 거짓 판단 식> else <거짓일 때 식>에 대응되는 넘파이 함수이다.

xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
cond = np.array([True, False, True, True, False])

각각의 성분에 대해서 cond이 True이면 xarr 원소를 그렇지 않으면 yarr 원소를 얻기를 원한다고 하자. 리스트 축약을 이용하면 다음과 같이 구할 수 있다.

[(x if c else y) for x, y, c in zip(xarr, yarr, cond)]

[1.1, 2.2, 1.3, 1.4, 2.5]

이 방법은 배열이 커지면 계산이 느려진다. 또한 다차원 배열에 대해서는 적용할 수 없다. np.where를 이용하면 간단히 계산할 수 있다.

result = np.where(cond, xarr, yarr)
result

array([1.1, 2.2, 1.3, 1.4, 2.5])

np.where의 두번째, 세번째 인자는 배열일 필요가 없이 스칼라여도 된다. 다음과 같이 4 x 4 무작위 배열에서 음수이면 -2, 그렇지않으면 2를 지정하려고 할 때 np.where를 사용하면 쉽게 할 수 있다.

arr = np.random.randn(4, 4)
arr

array([[-0.34791215,  0.15634897,  1.23029068,  1.20237985],
       [-0.38732682, -0.30230275, -1.04855297, -1.42001794],
       [-1.70627019,  1.9507754 , -0.50965218, -0.4380743 ],
       [-1.25279536,  0.77749036, -1.61389785, -0.21274028]])

np.where(arr < 0, -2, 2)

array([[-2,  2,  2,  2],
       [-2, -2, -2, -2],
       [-2,  2, -2, -2],
       [-2,  2, -2, -2]])

또한 배열과 스칼라를 동시에 사용할 수도 있다. 예를 들어 arr 배열 원소 중 양수만 2로 바꾸려면 다음과 같이 한다.

np.where(arr > 0, 2, arr)

array([[-0.34791215,  2.        ,  2.        ,  2.        ],
       [-0.38732682, -0.30230275, -1.04855297, -1.42001794],
       [-1.70627019,  2.        , -0.50965218, -0.4380743 ],
       [-1.25279536,  2.        , -1.61389785, -0.21274028]])

수학 및 통계 메소드

축 또는 전체 배열에 대한 통계를 구하는 메소드들이 배열 클래스를 통해 제공된다. std, sum, mean과 같은 집계(aggregation) 함수들은 넘파이 함수 또는 인스턴스의 메소드를 이용해 부를 수 있다. 다음과 같이 정규 분포로부터 무작위 수에 대한 배열을 만들자.

arr = np.random.randn(5, 4)
arr

array([[-1.63019835,  0.46278226, -0.90729836,  0.0519454 ],
       [ 0.72909056,  0.12898291,  1.13940068, -1.23482582],
       [ 0.40234164, -0.68481009, -0.87079715, -0.57884966],
       [-0.31155253,  0.05616534, -1.16514984,  0.90082649],
       [ 0.46566244, -1.53624369,  1.48825219,  1.89588918]])

arr.mean()

-0.059919320352960825

np.mean(arr)

-0.059919320352960825

arr.sum()

-1.1983864070592165

mean과 sum 같은 메소드는 선택인자로 축(axis=)을 가질 수 있다. axis=0란 다른 축은 고정시키고 첫번째 축(x축) 값에 대해서만 계산을 하라는 뜻이다.

arr.sum(axis=0)

array([-0.34465624, -1.57312327, -0.31559248,  1.03498557])

arr.sum(axis=1)

array([-2.02276906,  0.76264834, -1.73211526, -0.51971054,  2.31356012])

cumsum, cumprod 메소드는 집계 값을 반환하는 것이 아니라 집계 중간값이 포함된 같은 크기의 배열을 반환한다.

arr = np.arange(8)
arr

array([0, 1, 2, 3, 4, 5, 6, 7])

arr.cumsum()

array([ 0,  1,  3,  6, 10, 15, 21, 28], dtype=int32)

다차원 배열인 경우도 배열의 크기가 같은 중간 집계가 포함된 배열을 반환한다. 중간 집계 값들은 주어진 축에 대해서 계산된 것들이 저장된다.

arr = np.arange(9).reshape(3, 3)
arr

array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

arr.cumsum(axis=0)

array([[ 0,  1,  2],
       [ 3,  5,  7],
       [ 9, 12, 15]], dtype=int32)

arr.cumsum(axis=1)

array([[ 0,  1,  3],
       [ 3,  7, 12],
       [ 6, 13, 21]], dtype=int32)

다음은 기본 통계 함수들이다.

Method	Description
sum	Sum of all the elements in the array or along an axis; zero-length arrays have sum 0
mean	Arithmetic mean; zero-length arrays have NaN mean
std, var	Standard deviation and variance, respectively, with optional degrees of freedom adjustment (default denominator n)
min, max	Minimum and maximum
argmin, argmax	Indices of minimum and maximum elements, respectively
cumsum	Cumulative sum of elements starting from 0
cumprod	Cumulative product of elements starting from 1

논리 배열 메소드

앞에서 살펴보았던 메소드들은 논리형 True, False를 가각 숫자 1과 0으로 변환해서 계산한다.

arr = np.random.randn(10)
arr

array([ 0.01050002,  1.78587049,  0.12691209,  0.40198936,  1.8831507 ,
       -1.34775906, -1.270485  ,  0.96939671, -1.17312341,  1.94362119])

0보다 큰 숫자들의 논리 배열은 다음과 같다.

arr > 0

array([ True,  True,  True,  True,  True, False, False,  True, False,
        True])

이 배열에 sum 메소드를 사용하면 참인 것의 갯수를 셀 수 있다.

(arr > 0).sum()

7

이 밖에도 자주 사용되는 유용한 메소드로 any와 all이 있다. any는 배열 중 참(True)인 것이 하나라도 있으면 참을 반환하고 all은 배열이 모두 참으로만 이루어졌을 때 참(True)을 반환한다.

any(arr > 0)

True

all(arr > 0)

False

정렬

파이썬 리스트 메소드 sort와 비슷하게 넘파이 배열도 sort 메소드를 이용해서 정렬을 할 수 있다.

arr = np.random.randn(5)
arr

array([ 0.40746184, -0.76991607,  0.53924919, -0.67433266,  0.03183056])

sort는 리스트에서와 마찬가지로 배열 자신을 변경한다.

arr.sort()
arr

array([-0.76991607, -0.67433266,  0.03183056,  0.40746184,  0.53924919])

다차원 배열은 축 선택을 통해서 정렬을 할 수 있다.

arr = np.random.randn(3, 5)
arr

array([[-1.22543552,  0.84436298, -1.00021535, -1.5447711 ,  1.18802979],
       [ 0.31694261,  0.92085882,  0.31872765,  0.85683061, -0.65102559],
       [-1.03424284,  0.68159452, -0.80340966, -0.68954978, -0.4555325 ]])

arr.sort(axis=1)
arr

array([[-1.5447711 , -1.22543552, -1.00021535,  0.84436298,  1.18802979],
       [-0.65102559,  0.31694261,  0.31872765,  0.85683061,  0.92085882],
       [-1.03424284, -0.80340966, -0.68954978, -0.4555325 ,  0.68159452]])

유일성 및 집합 연산

numpy.unique 함수를 이용해서 배열 원소중 중복되지 않는 배열을 얻을 수 있다. unique 결과값은 항상 1차원 배열이다.

names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
np.unique(names)

array(['Bob', 'Joe', 'Will'], dtype='<U4')

순수 파이썬만을 이용하면 다음과 같이 쓸 수 있다.

sorted(set(names))

['Bob', 'Joe', 'Will']

한 배열의 원소들이 다른 배열에 속했는지를 판단할 수 있는 함수로 np.in1d가 있다.

values = np.array([6, 0, 0, 3, 2, 5, 6])

np.in1d(values, [1, 2, 3])

array([False, False, False,  True,  True, False, False])

다음은 집합에 대한 연산이다.

Method	Description
unique(x)	Compute the sorted, unique elements in x
intersect1d (x, y)	Compute the sorted, common elements in x and y
union1d(x, y)	Compute the sorted union of elements
in1d(x, y)	Compute a boolean array indicating whether each element of x is contained in y
setdiff1d(x , y)	Set difference, elements in x that are not in y
setxor1d(x, y)	Set symmetric differences; elements that are in either of the arrays, but not both

넘파이 배열 파일 입출력

넘파이는 텍스트및 바이너리 파일로 입력과 출력을 할 수 있다. 여기서는 넘파이 바이너리 입출력만 알아본다. 일반적으로 판다스 입출력 메소드들을 이용하면 쉽게 자료들을 다룰 수 있다.

np.save(파일이름, 배열), np.load(파일이름)을 이용해서 파일로 저장 및 파일에서 불러오기를 한다. 배열은 기본적으로 압축되지 않은 바이너리 형태로 저장이 되고 확장자는 .npy이다.

arr = np.arange(10)
np.save('examples/array_save', arr)

examples/array_save.npy 파일로 저장이 된다. 불러오려면 np.load를 다음과 같이 한다. 불러올 때는 확장자를 반드시 붙여야 한다.

arr1 = np.load('examples/array_save.npy')
arr1

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

여러 개의 배열 객체를 하나의 파일에 저자하려면 np.savez 함수를 이용한다. 기본 확장자는 .npz이다.

np.savez('examples/multi_array', a=arr, b=arr)

np.load를 이용해서 파일을 불러온다.

arr2 = np.load('examples/multi_array.npz')

불러온 객체의 배열을 접근하려면 저장할 때 사용한 열쇠(key)를 이용해서 사전형식으로 부른다.

arr2['a']

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

만일 저장할 때 열쇠를 지정하지 않았으면 기본적으로 'arr_0', 'arr_1' 열쇠를 사용하면 된다. 압축률이 높은 자료에 대해서는 np.savez_compressed 함수를 사용해도 된다.

선형대수

MATLAB과 같은 언어는 곱하기 연산자 *는 행렬곱인 반면에 넘파이에서는 두 배열간의 성분끼리 곱하기이다. 넘파이 행렬곱 연산은 dot 함수를 이용한다.

A = np.array([[1., 2., 3.], [4., 5., 6.]])
A

array([[1., 2., 3.],
       [4., 5., 6.]])

B = np.array([[6., 23.], [-1, 7], [8, 9]])
B

array([[ 6., 23.],
       [-1.,  7.],
       [ 8.,  9.]])

A.dot(B)

array([[ 28.,  64.],
       [ 67., 181.]])

또는 np.dot(A,B)를 사용해도 된다.

np.dot(A, B)

array([[ 28.,  64.],
       [ 67., 181.]])

파이썬 3.5부터는 @ 기호를 이용해서 행렬곱을 사용할 수 있게 되었다.

A @ B

array([[ 28.,  64.],
       [ 67., 181.]])

numpy.linalg 모듈은 역행렬, 행렬식(determinant) 및 분해(decomposition) 함수들을 포함하고 있다.

from numpy.linalg import inv, qr

X = np.random.randn(3, 3)
mat = X.T @ X
mat

array([[ 1.24382488,  2.28926321, -0.36487068],
       [ 2.28926321,  5.14666053,  1.59292516],
       [-0.36487068,  1.59292516,  5.61010504]])

inv_mat = inv(mat)
inv_mat

array([[ 2647.48784774, -1349.50625864,   555.3644981 ],
       [-1349.50625864,   688.09800762,  -283.14690842],
       [  555.3644981 ,  -283.14690842,   116.69443851]])

mat @ inv_mat

array([[ 1.00000000e+00, -3.54004792e-14,  1.83332514e-13],
       [ 3.32600392e-13,  1.00000000e+00,  1.03184050e-13],
       [-1.51012020e-13,  8.87059356e-14,  1.00000000e+00]])

다음은 QR 분해를 한 것이다.

q, r = qr(mat)
r

array([[-2.63077117e+00, -5.33998988e+00, -4.35547903e-01],
       [ 0.00000000e+00, -2.39807409e+00, -5.82701598e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.57677035e-03]])

다음은 많이 사용되는 함수들이다.

Function	Description
diag	Return the diagonal (or off-diagonal) elements of a square matrix as a 1D array, or convert a 1D array into a square matrix with zeros on the off-diagonal
dot	Matrix multiplication
trace	Compute the sum of the diagonal elements
det	Compute the matrix determinant
eig	Compute the eigenvalues and eigenvectors of a square matrix
inv	Compute the inverse of a square matrix
pinv	Compute the Moore-Penrose pseudo-inverse of a matrix
qr	Compute the QR decomposition
svd	Compute the singular value decomposition (SVD)
solve	Solve the linear system Ax = b for x, where A is a square matrix
lstsq	Compute the least-squares solution to Ax = b

의사 난수 생성(Pseudorandom Number Generation)

numpy.random 모듈은 파이썬 내장 모듈 random 기능들을 포함하여 다양한 분포에 대한 난수 생성 함수들을 제공한다. 4 x 4 배열의 난수를 표준 정규분포에서 구하고 싶으면 normal 함수를 사용하면 된다.

samples = np.random.normal(size=(4, 4))
samples

array([[-1.42406091, -0.49331988, -0.54286148,  0.41605005],
       [-1.15618243,  0.7811981 ,  1.49448454, -2.06998503],
       [ 0.42625873,  0.67690804, -0.63743703, -0.39727181],
       [-0.13288058, -0.29779088, -0.30901297, -1.67600381]])

여기서 사용하는 난수는 의사 난수라고 한다. 왜냐면 난수 생성은 seed와 알고리즘에 의해서 만들어지기 때문에 같은 seed와 알고리즘하에서는 항상 같은 난수가 만들어지기 때문이다. 난수 발생을 국한적으로 사용하고 싶으면 RandomState 메소드를 사용하면 된다.

rng = np.random.RandomState(1234)
rng.randn(10)

array([ 0.47143516, -1.19097569,  1.43270697, -0.3126519 , -0.72058873,
        0.88716294,  0.85958841, -0.6365235 ,  0.01569637, -2.24268495])

Function	Description
seed	Seed the random number generator
permutation	Return a random permutation of a sequence, or return a permuted range
shuffle	Randomly permute a sequence in-place
rand	Draw samples from a uniform distribution
randint	Draw random integers from a given low-to-high range
randn	Draw samples from a normal distribution with mean 0 and standard deviation 1 (MATLAB-like interface)
binomial	Draw samples from a binomial distribution
normal	Draw samples from a normal (Gaussian) distribution
beta	Draw samples from a beta distribution
chisquare	Draw samples from a chi-square distribution
gamma	Draw samples from a gamma distribution
uniform	Draw samples from a uniform [0, 1) distribution

Example: Random Walks

생략