배열 연산 및 플롯

파이썬 배열(array)이란 파이썬 리스트와 비슷하지만 더 제한적이지만 훨씬 효율적 계산을 하기 위한 용도입니다. 수식 계산을 할 때 많은 양의 숫자들을 이용한 연산이 필요합니다. 일반적인 프로그래밍에서 리스트는 여러 가지 다양한 객체들을 담을 수 있어서 편리하지만 수식 계산을 하기에는 효율적이지 않습니다. 일반적으로 과학 계산을 할 때는 숫자들로만 이루어져있고 숫자의 타입도 정해져 있어서 저장이나 계산할 때는 정해진 크기에 따라 계산되므로 훨씬 더 효율적으로 계산이 가능합니다.

이런 용도로 과학 계산 용도로 개발된 패키지가 numpy 입니다. 이 장에서는 numpy를 이용해서 배열을 만들고 사용하는 방법에 대해서 알아봅니다.

벡터

벡터 개념

수학에서 벡터는 2차원은 \((x, y)\), 3차원은 \((x, y, z)\)와 같이 표현되며 n차원은 \((x_1, x_2, \ldots, x_n)\) 과 같이 표현됩니다.

파이썬에서 벡터는 리스트 또는 튜플을 이용해서 표현할 수 있습니다.

v1 = [x, y]
v2 = (-1, 2)
v3 = (x1, x2, x3)
import math
v4 = [math.exp(-i * 0.1) for i in range(10)]

벡터 연산

\[(u_1, u_2) \pm (v_1, v_2) = (u_1 \pm v_1, u_2 \pm v_2)\]

스칼라 \(k\)에 대해서 스칼라 곱은 다음과 같습니다.

\[k (v_1, v_2 ) = (kv_1, kv_2)\]

내적은 다음과 같이 정의됩니다.

\[(u_0, u_1, \ldots, u_{n-1}) \cdot (v_0, v_1, \ldots, v_{n-1}) = u_0v_0 + u_1v_1 + \cdots + u_{n-1} v_{n-1} = \sum_{i=0}^{n-1} u_i v_i\]

벡터의 크기는 다음과 같이 정의됩니다.

\[\|(u_0, u_1, \ldots, u_{n-1}) \| = \sqrt{u_0^2 + u_1^2 + \cdots + u_{n-1}^2} = \sqrt{\sum_{i=0}^{n-1} u_i^2}\]

벡터 함수

\(f(x)\) 가 실수값을 갖는 함수라고 하면 이 실함수에 벡터 \(v = (v_0, v_1, \ldots, v_{n-1})\)을 적용하는 함수 \(f(v)\) 는 다음과 같이 정의합니다.

\[f(v) = (f(v_0), f(v_1), \ldots, f(v_{n-1}))\]

수학 벡터함수로 표현하자면 다음과 같이 할 수도 있습니다.

\[\begin{split}\mathbf{f}: R^n \to R^n \\ \mathbf{f}(v) = (f_0(v), f_1(v), \ldots, f_{n-1}(v)) \\ f_i(v) = f(v_i) \quad i = 0, 1, \ldots, n-1\end{split}\]

예를 들면

\[\sin(v) = (\sin(v_0), \sin(v_1), \ldots, \sin(v_{n-1}))\]

거듭제곱도 다음과 같이 정의합니다.

\[v^b = (v_0^b, v_1^b, \ldots, v_{n-1}^b)\]

성분끼리 곱도 다음과 같이 정의합니다.

\[u \ast v = (u_0 v_0, u_1 v_1, \ldots, u_{n-1} v_{n-1})\]

스칼라 \(a\)와 벡터 \(v\)의 합도 다음과 같이 정의합니다.

\[a + v = (a+v_0, a+v_1, \ldots, a+v_{n-1})\]

다음과 같이 결합된 연산도 수식 연산 순위와 같이 계산합니다.

\[v^2 \ast \cos(v) \ast e^v + 2\]

위 연산을 한 결과는 다음과 같습니다.

\[(v_0^2 \cos(v_0) e^{v_0} +2, \ldots, v_{n-1}^2 \cos(v_{n-1}) e^{v_{n-1}} +2)\]

위의 계산을 다음과 같이 함수를 이용하여 표현할 수 있습니다.

\[f(x) = x^2 \cos(x) e^x + 2\]

즉 \(f(v)\)로 표현할 수 있습니다.

넘파이 배열

리스트 이용

n 개의 값 \(x_0\), \(x_1\), \(\ldots\), \(x_{n-1}\)에서 함수값 \(f(x_0)\), \(f(x_1)\), \(\ldots\), \(f(x_{n-1})\)들을 리스트를 이용해서 다룰 수 있습니다.

다음은 \(f(x) = x^3\) 함수값을 \([0, 1]\) 구간을 5개의 균등점에서 구한 것입니다.

In [1]: def f(x):
   ...:   return x ** 3
   ...: 
   ...: n = 5
   ...: dx = 1 / (n-1) # 간격
   ...: xlist = [i * dx for i in range(n)] # x 리스트
   ...: ylist = [f(x) for x in xlist] # f(x) 리스트
   ...: pairs = [[x, y] for x, y in zip(xlist, ylist)] # (x, f(x)) 리스트
   ...: 

직접하기

• \(f(x) = x^2 \sin(x)\) 함수를 구간 \([0, \pi]\) 에서 30개의 균등점에서 \((x, f(x))\) 리스트를 구하시오.

넘파이 배열

넘파이 배열은 다음과 같은 가정과 특징들을 가지고 있습니다.

• 배열의 모든 원소의 타입은 같습니다. 과학 계산을 위해서 보통 정수형, 실수형, 복소수형들이 사용됩니다.

• 배열이 만들어질 때 배열의 원소의 갯수는 결정되어야 합니다.

• 배열은 파이썬 표준에 속하지 않아 과학 계산 패키지(numerical python)를 불러와서 사용해야 합니다. 이 패키지 이름은 numpy(넘파이)로 import를 이용해서 사용합니다.

• 넘파이는 벡터 연산을 할 수 있어서 for 문과 같은 반복문이 거의 필요없습니다.

• 배열은 인덱스를 이용해서 접근할 수 있으며 배열의 크기에 따라 인덱스의 차원도 결정됩니다.

일반적으로 넘파이는 다음과 같이 불러올 수 있습니다.

In [2]: import numpy as np

리스트를 넘파이 배열로 변환하는 방법은 다음과 같습니다.

In [3]: r = [1, 2, 3]
   ...: a = np.array(r)
   ...: a
   ...: 
Out[3]: array([1, 2, 3])

n 개의 0으로 이루어진 배열은 zeros 함수를 이용할 수 있습니다.

In [4]: n = 10
   ...: np.zeros(n)
   ...: 
Out[4]: array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

넘파이 배열과 같은 크기의 0들로 이루어진 새로운 배열은 zeros_like 함수를 사용하여 만들 수 있습니다.

In [5]: np.zeros_like(a)
Out[5]: array([0, 0, 0])

주어진 구간에서 같은 간격으로 이루어진 n개의 점을 구할 때 linspace 함수를 사용할 수 있습니다. 다음은 구간 [0, 1]을 같은 간격으로 11개의 점을 구하는 것입니다.

In [6]: a = np.linspace(0, 1, 11)
   ...: a
   ...: 
Out[6]: array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ])

배열의 성분들은 파이썬 슬라이싱을 이용해서 접근할 수 있습니다.

In [7]: b = a[1:-1]
   ...: b
   ...: 
Out[7]: array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])

인덱싱을 이용해서 얻어진 배열은 새로운 배열이 아니라 원래 배열의 뷰(view)입니다. 따라서 인덱승해서 얻어진 배열의 값을 바꾸면 원래 배열의 위치에 있는 값도 같이 바뀝니다.

In [8]: b[0] = 100
   ...: a
   ...: 
Out[8]: 
array([  0. , 100. ,   0.2,   0.3,   0.4,   0.5,   0.6,   0.7,   0.8,
         0.9,   1. ])

위에서 b[0]는 a[1] 과 같은 곳을 가리키고 있으므로 b[0]의 값을 바꾸면 a[1]의 값이 변경되게 됩니다.

파이썬 인덱스 슬라이싱과 마찬가지로 다음과 같은 것이 성립합니다.

In [9]: a[1:-1:2]
Out[9]: array([100. ,   0.3,   0.5,   0.7,   0.9])

직접하기

• a[::3]이 의미하는 것은 무엇입니까?

• a[-1::-2]가 의미하는 것은 무엇입니까?

• a[-1:2:-2][1]이 의미하는 것은 무엇입니까?

좌표와 함수값

앞에서 리스트를 이용해서 했던 함수 리스트를 구하는 것을 넘파이 배열을 이용해서 할 수 있습니다.

다음은 이미 만들어진 리스트를 이용해서 넘파이 배열로 변환하는 것입니다.

In [10]: import numpy as np
   ....: 
   ....: x2 = np.array(xlist)
   ....: y2 = np.array(ylist)
   ....: print(x2, y2)
   ....: 
[0.   0.25 0.5  0.75 1.  ] [0.       0.015625 0.125    0.421875 1.      ]

직접 넘파이 배열로 만들어 사용할 수 있습니다. for 문을 이용해서 함수값 배열을 만들 수 있습니다.

In [11]: n = len(xlist)
   ....: x2 = np.linspace(0, 1, n)
   ....: y2 = np.zeros(n)
   ....: for i in range(n):
   ....:   y2[i] = f(x2[i])
   ....: y2
   ....: 
Out[11]: array([0.      , 0.015625, 0.125   , 0.421875, 1.      ])

더 간단하게 리스트 축약을 이용할 수 있습니다.

In [12]: y2 = np.array([f(xi) for xi in x2])
   ....: y2
   ....: 
Out[12]: array([0.      , 0.015625, 0.125   , 0.421875, 1.      ])

하지만 넘파이 함수들을 이용하면 더 빠르고 간단하게 배열을 만들 수 있습니다.

벡터화

커다란 배열에 대한 반복문은 실행속도가 늦어질 수 있습니다. 넘파이 배열의 장점으로 배열을 함수에 적용하면 각각에 대한 함수값의 배열이 계산되어 반환된다는 것입니다.

즉, 위의 반복문을 이용해서 함수값 배열을 구하는 것을 간단히 배열을 함수의 인자로 넘겨주면 자동으로 배열이 계산되어 나옵니다.

In [13]: y2 = f(x2)
   ....: y2
   ....: 
Out[13]: array([0.      , 0.015625, 0.125   , 0.421875, 1.      ])

벡터 함수에서 설명했던 함수값 계산이 자동으로 됩니다. 함수 f를 호출하지 않고 직접 x ** 3을 입력해도 됩니다.

math 패키지 함수들 sin, cos, exp과 마찬가지로 똑같이 넘파이 함수들이 정의되어 있습니다. math 패키지와 다른 점은 벡터 계산이 된다는 것입니다.

다음과 같이 math 패키지의 함수들은 벡터 계산이 불가능합니다.

In [14]: import math
   ....: math.sin(x2)
   ....: 
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-14-4eff1241a199> in <module>
      1 import math
----> 2 math.sin(x2)

TypeError: only size-1 arrays can be converted to Python scalars

하지만 넘파이 함수들은 가능합니다.

In [15]: np.sin(x2)
Out[15]: array([0.        , 0.24740396, 0.47942554, 0.68163876, 0.84147098])

넘파이 배열을 이용해서 다음 함수의 값을 구하는 것입니다.

\[f(x) = \sin(\pi x) \cos(x) e^{-x^2} + 2 + x^2\]

In [16]: x = np.linspace(0, 2, 21)
   ....: np.sin(np.pi * x) * np.cos(x) * np.exp(-x ** 2) + 2 + x ** 2
   ....: 
Out[16]: 
array([2.        , 2.31441379, 2.5934807 , 2.79636229, 2.90646182,
       2.93346199, 2.90763462, 2.86907503, 2.85593359, 2.89545192,
       3.        , 3.16820201, 3.3895371 , 3.65006793, 3.93723047,
       4.24254435, 4.56214678, 4.89579312, 5.24523018, 5.61270253,
       6.        ])

np.sin(np.pi * x) * np.cos(x) * np.exp(-x ** 2) + 2 + x ** 2와 같이 계산하는 것을 벡터화 계산이라고 합니다. 반면에 성분 하나 하나에 대해서 계산하는 코드를 스칼라 코드라고 합니다.

함수 \(xe^{-x}\) 값 계산 스칼라 코드 예제는 다음과 같습니다.

import numpy as np
import math

N = 21
x = np.zeros(N)
y = np.zeros(N)
dx = 2.0 / (N-1) # x 좌표 구간

for i in range(N):
  x[i] = -1 + dx * i
  y[i] = math.exp(-x[i]) * x[i]

위 코드의 벡터화 코드는 다음과 같습니다.

x = np.linspace(-1, 1, N)
y = np.exp(-x) * x

곡선 플롯

좌표 평면에 함수 \(y = f(x)\) 그래프를 컴퓨터를 이용해서 그리는 것을 플롯(plot)이라고 합니다.

플롯은 주어진 점들을 직선으로 연결하는 것입니다. 많은 점들로 이루어진 것을 직선으로 연결하면 부드러운 곡선 모양으로 보입니다.

곡선을 플롯하기 위해서는 정해진 구간 [a, b] 에서 정의된 (x, y) 순서쌍이 필요합니다. 순서쌍은 일반적으로 구간을 일정하게 나눈 점들에서 함수값들을 구하여 만듭니다. 즉

\[x_i = a + i h, \quad h = \frac{b-a}{n-1}\]

를 만들고 \(y_i = f(x_i)\)를 이용해서 구합니다. 그리고 플롯하기 위해서는 plot(x, y) 와 같은 명령어를 사용합니다.

matplotlib 이용

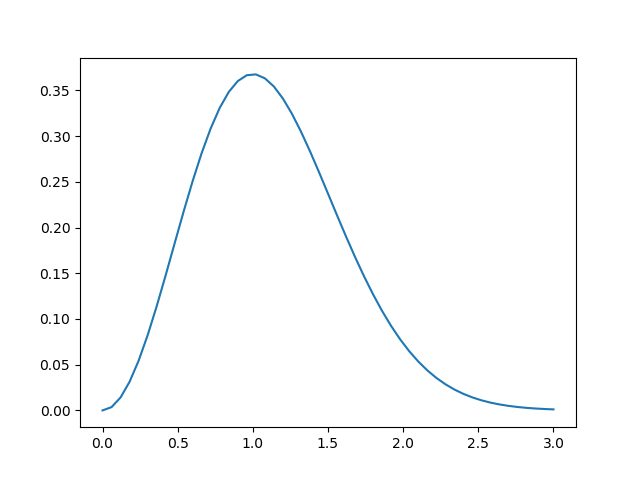
[0, 3] 사이의 51 개의 점을 이용해서 \(f(t) = t^2 e^{-t^2}\) 함수의 그래프를 그리려고 합니다.

In [17]: import numpy as np
   ....: import matplotlib.pyplot as plt
   ....: 
   ....: def f(t):
   ....:   return t ** 2 * np.exp(-t ** 2)
   ....: 
   ....: t = np.linspace(0, 3, 51)
   ....: y = f(t)
   ....: 
   ....: plt.plot(t, y)
   ....: # plt.show()
   ....: 
Out[17]: [<matplotlib.lines.Line2D at 0x1f0f120e5f8>]

다음과 같이 그림을 저장할 수 있습니다.

plt.savefig('tmp.pdf')

플롯 꾸미기

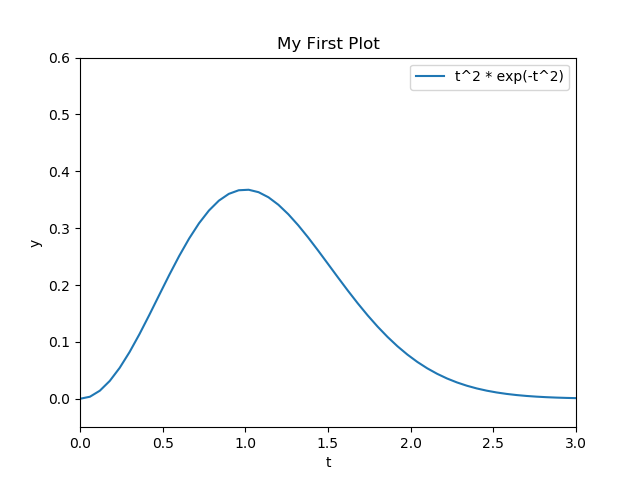
plt.xlabel(), plt.ylabel()을 이용하여 각 축의 레이블을 설정할 수 있습니다. plt.plot()의 label 옵션과 plt.legend()를 이용하여 범례를 달 수 있습니다. plt.axis()를 이용하여 보여지는 범위를 설정할 수 있습니다. plt.title()을 이용하여 그림의 제목을 설정합니다.

In [18]: plt.plot(t, y, label='t^2 * exp(-t^2)')
   ....: 
   ....: plt.xlabel('t')
   ....: plt.ylabel('y')
   ....: plt.legend()
   ....: plt.axis([0, 3, -0.05, 0.6]) # [xmin, xmax, ymin, ymax]
   ....: plt.title('My First Plot')
   ....: 
Out[18]: Text(0.5, 1.0, 'My First Plot')

여러 개의 플롯

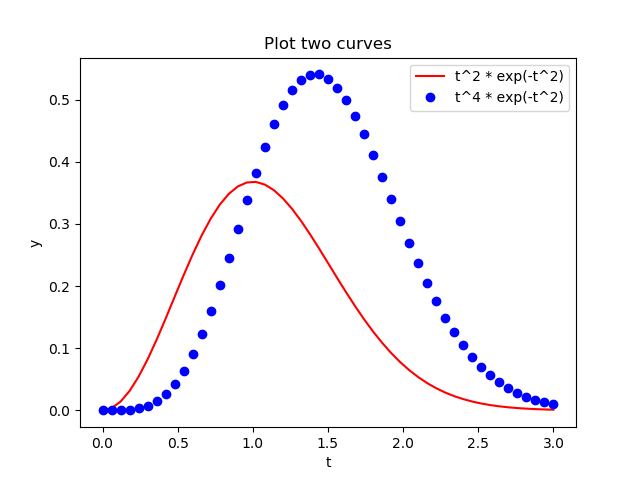
여러 개의 플롯을 하나의 창에 그릴 수 있습니다. \(f(t)\)와 \(f_2(t) = t^4 e^{-t^2}\) 을 함께 그립니다. r- 옵션은 선색은 빨강, 마커 스타일은 실선을 의미하고 bo 옵션은 선색은 파랑, 마커 스타일은 원을 의미합니다. 자세한 마커 스타일은 이곳을 참조하세요.

In [19]: def f2(t):
   ....:   return t ** 2 * f(t)
   ....: 
   ....: t = np.linspace(0, 3, 51)
   ....: y1 = f(t)
   ....: y2 = f2(t)
   ....: 
   ....: plt.plot(t, y1, 'r-', label='t^2 * exp(-t^2)')
   ....: plt.plot(t, y2, 'bo', label='t^4 * exp(-t^2)')
   ....: 
   ....: plt.xlabel('t')
   ....: plt.ylabel('y')
   ....: plt.legend()
   ....: plt.title('Plot two curves')
   ....: 
Out[19]: Text(0.5, 1.0, 'Plot two curves')

여러 개의 축들(Axes)

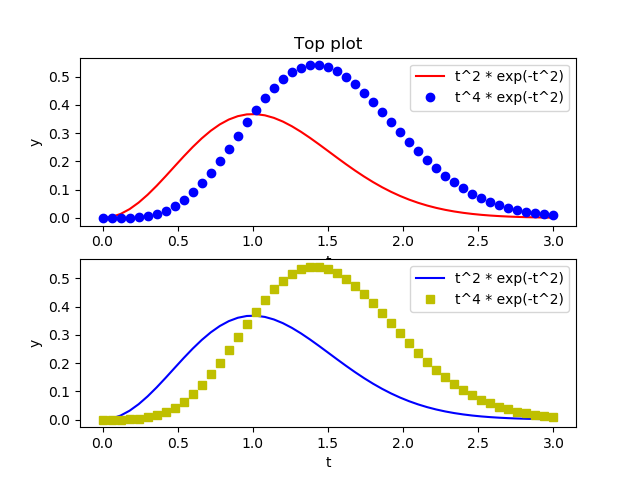
matplotlib는 기본적으로 Figure와 Axes로 이루어집니다. 자세한 것은 Artist Tutorial을 참조하세요. Figure는 하나의 창을 의미한다고 보면 되고 Axes 그 창 안에 그려지는 네모난 사각형에 그려지는 그림들이라고 생각하시면 됩니다. Figure는 여러 개의 축(Axes)들로 이루어 질 수 있습니다. 하나의 Figure에 여러 개의 축들을 담기 위해서는 plt.subplot() 을 이용하면 됩니다.

In [20]: plt.subplot(2, 1, 1)
   ....: 
   ....: plt.plot(t, y1, 'r-', label='t^2 * exp(-t^2)')
   ....: plt.plot(t, y2, 'bo', label='t^4 * exp(-t^2)')
   ....: plt.xlabel('t')
   ....: plt.ylabel('y')
   ....: plt.title('Top plot')
   ....: plt.legend()
   ....: 
   ....: plt.subplot(2, 1, 2)
   ....: 
   ....: plt.plot(t, y1, 'b-', label='t^2 * exp(-t^2)')
   ....: plt.plot(t, y2, 'ys', label='t^4 * exp(-t^2)')
   ....: plt.xlabel('t')
   ....: plt.ylabel('y')
   ....: plt.legend()
   ....: 
Out[20]: <matplotlib.legend.Legend at 0x1f0f1403cf8>

애니메이션

다음은 정규분포 확률밀도함수입니다. s는 분산, m은 평균입니다.

\[f(x; m, s) = (2\pi)^{-1/2}s^{-1} \exp\left[-\frac{1}{2}\left(\frac{x-m}{s}\right)^2\right]\]

s가 변하면서 그래프의 모양이 어떻게 바뀌는지를 보는 것입니다.

다음 코드는 분산이 변할 때 각각의 플롯을 파일로 저장하는 것입니다. tmp 폴더를 만들고 그곳에 30개의 파일을 저장합니다.

In [21]: import os
   ....: 
   ....: if not os.path.exists('tmp'):
   ....:   os.mkdir('tmp') # 임시 폴더 생성
   ....: 
   ....: def f_norm(x, m, s):
   ....:   return (1 / (np.sqrt(2 * np.pi) * s)) * np.exp(-0.5 * ((x - m) / s) ** 2)
   ....: 
   ....: m = 0
   ....: s_min = 0.2
   ....: s_max = 2
   ....: x = np.linspace(m - 3 * s_max, m + 3 * s_max, 1000)
   ....: s_values = np.linspace(s_max, s_min, 30)
   ....: max_f = f_norm(m, m, s_min)
   ....: 
   ....: plt.ion()
   ....: 
   ....: y = f_norm(x, m, s_max)
   ....: lines = plt.plot(x, y)
   ....: plt.axis([x[0], x[-1], -0.1, max_f])
   ....: plt.xlabel('x')
   ....: plt.ylabel('f')
   ....: 
   ....: counter = 0
   ....: for s in s_values:
   ....:   y = f_norm(x, m, s)
   ....:   lines[0].set_ydata(y)
   ....:   plt.legend(['s={:4.2f}'.format(s)])
   ....:   plt.draw()
   ....:   plt.savefig('tmp/tmp{:04d}.png'.format(counter))
   ....:   counter += 1
   ....:   plt.pause(0.05)
   ....: 

Jupyter Notebook에서는 다음 코드를 실행합니다.

%matplotlib notebook

import os
import matplotlib.pyplot as plt
import numpy as np

if not os.path.exists('tmp'):
    os.mkdir('tmp') # 임시 폴더 생성

def f_norm(x, m, s):
    return (1 / (np.sqrt(2 * np.pi) * s)) *   np.exp(-0.5 * ((x - m) / s) ** 2)

m = 0
s_min = 0.2
s_max = 2
x = np.linspace(m - 3 * s_max, m + 3 * s_max,   1000)
s_values = np.linspace(s_max, s_min, 30)
max_f = f_norm(m, m, s_min)

y = f_norm(x, m, s_max)

fig, ax = plt.subplots()

lines = ax.plot(x, y)
ax.axis([x[0], x[-1], -0.1, max_f])
ax.set_xlabel('x')
ax.set_ylabel('f')

counter = 0
for s in s_values:
    y = f_norm(x, m, s)
    lines[0].set_xdata(x)
    lines[0].set_ydata(y)
    ax.legend(['s={:4.2f}'.format(s)])

    fig.canvas.draw()
    fig.savefig('tmp/tmp{:04d}.png'.format  (counter))

    counter += 1
    plt.pause(0.05)

matplotlib FuncAnimation 이용

In [22]: from matplotlib.animation import FuncAnimation
   ....: 
   ....: fig, ax = plt.subplots()
   ....: ax.axis([x[0], x[-1], -0.1, max_f])
   ....: lines = ax.plot([], [])
   ....: ax.set_xlabel('x')
   ....: ax.set_ylabel('f')
   ....: 
   ....: def init():
   ....:   lines[0].set_data([], [])
   ....:   return lines
   ....: 
   ....: def frame(args):
   ....:   frame_no, s, x, lines = args
   ....:   y = f_norm(x, m, s)
   ....:   lines[0].set_data(x, y)
   ....:   return lines
   ....: 
   ....: all_args = [(frame_no, s, x, lines)
   ....: anim = FuncAnimation(fig, frame, all_args, interval=150, init_func=init, blit=True)
   ....: 
          for frame_no, s in enumerate(s_values)]

주피터 노트북에서는 다음 코드를 실행합니다.

%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import rc
from IPython.display import HTML
from matplotlib.animation import FuncAnimation

def f_norm(x, m, s):
    return (1 / (np.sqrt(2 * np.pi) * s)) * np.exp(-0.5 * ((x - m) / s) ** 2)

m = 0
s_min = 0.2
s_max = 2
x = np.linspace(m - 3 * s_max, m + 3 * s_max, 1000)
s_values = np.linspace(s_max, s_min, 30)
max_f = f_norm(m, m, s_min)

fig, ax = plt.subplots()
ax.axis([x[0], x[-1], -0.1, max_f])
lines = ax.plot([], [])
ax.set_xlabel('x')
ax.set_ylabel('f')

def init():
    lines[0].set_data([], [])
    return lines

def frame(args):
    frame_no, s, x, lines = args
    y = f_norm(x, m, s)
    lines[0].set_data(x, y)
    return lines

all_args = [(frame_no, s, x, lines) for frame_no, s in enumerate(s_values)]

anim = FuncAnimation(fig, frame, all_args, interval=150, init_func=init, blit=True)
HTML(anim.to_html5_video())

만일 다음과 같은 에러가 발생하면 ffmpeg을 설치합니다.

RuntimeError: Requested MovieWriter (ffmpeg) not available

conda-forge에서 설치를 합니다.

conda install -c conda-forge ffmpeg

동영상으로 저장하려면 다음과 같이 합니다.

anim.save('tmp.mp4')

플롯 어려움

조각 함수

계단함수

\[\begin{split}H(x) = \begin{cases} 0, & x < 0 \\ 1, & x \ge 0 \end{cases}\end{split}\]

9개의 점으로 그려지는 계단함수입니다.

In [23]: def H(x):
   ....:   return np.where(x < 0, 0, 1)
   ....: 
   ....: x = np.linspace(-10, 10, 9)
   ....: plt.plot(x, H(x))
   ....: plt.grid()
   ....: 

51개의 점으로 그려지는 계단함수입니다.

In [24]: x = np.linspace(-10, 10, 51)
   ....: plt.plot(x, H(x))
   ....: plt.grid()
   ....: 

정확하게 그리려면 다음과 같이 해야 합니다.

In [25]: plt.plot([-10, 0, 0, 10], [0, 0, 1, 1])
   ....: plt.grid()
   ....: 

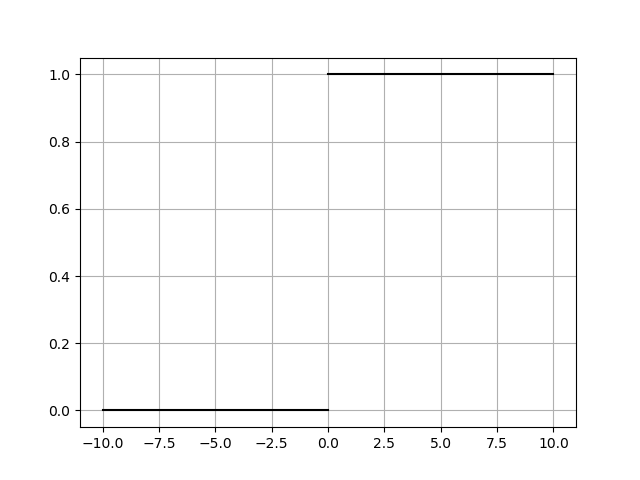
더 엄격하게 하려면 두 개의 직선을 그려야 합니다.

In [26]: plt.plot([-10, 0], [0, 0], 'k', [0, 10], [1, 1], 'k')
   ....: plt.grid()
   ....: 

진동함수

\[f(x) = \sin(1/x)\]

다음은 fig, ax = plt.subplots(nrow, ncol) nrow 개의 행, ncol 개의 열을 갖는 축들을 만들고 ax에 배열로 반환합니다.

In [27]: f = lambda x: np.sin(1 / x)
   ....: 
   ....: x1 = np.linspace(-1, 1, 10)
   ....: x2 = np.linspace(-1, 1, 1000)
   ....: 
   ....: fig, ax = plt.subplots(1, 2)
   ....: 
   ....: ax[0].plot(x1, f(x1))
   ....: ax[0].grid()
   ....: 
   ....: ax[1].plot(x2, f(x2))
   ....: ax[1].grid()
   ....: 

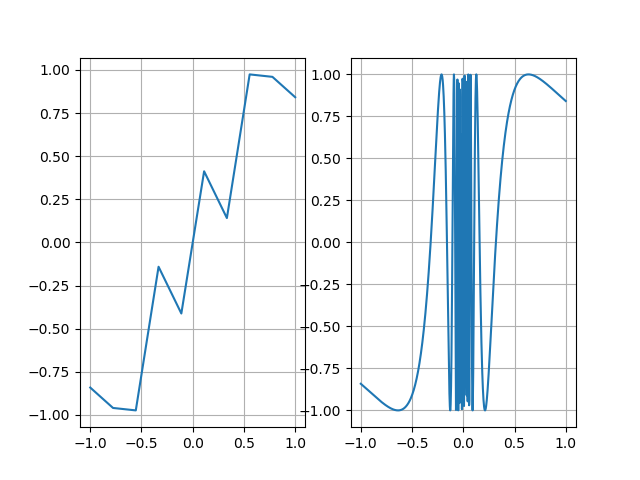
향상된 벡터함수

계단함수를 다음과 같이 구현해봅니다.

In [28]: def step(x):
   ....:   return (0 if x < 0 else 1)
   ....: 
   ....: x = np.linspace(-10, 10, 5)
   ....: x
   ....: 
Out[28]: array([-10.,  -5.,   0.,   5.,  10.])

그리고 함수를 실행하면 다음과 같은 에러가 납니다.

In [29]: step(x)
---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-29-3589212b11a2> in <module>
----> 1 step(x)

<ipython-input-28-68441e286f65> in step(x)
      1 def step(x):
----> 2   return (0 if x < 0 else 1)
      3 
      4 x = np.linspace(-10, 10, 5)
      5 x

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

에러가 나는 이유는 x는 넘파이 배열인데 step(x)에서 처리하는 if 문은 배열을 처리할 수 없기 때문에 발생합니다.

if 문 안에 부등호 x < 0를 보면 True, False 배열이 나오는 것을 알 수 있습니다.

In [30]: x < 0
Out[30]: array([ True,  True, False, False, False])

여기서 살펴볼 것은 논리형 배열에 숫자 연산을 하면 자동으로 논리 배열은 0 또는 1로 바꾸어 계산이 됩니다. True는 1이고 False는 0으로 바꿉니다.

In [31]: tf = x < 0
   ....: tf * 1
   ....: 
Out[31]: array([1, 1, 0, 0, 0])

이것을 해결하는 방안으로 여러 가지가 있겠지만 넘파이에서는 이런한 배열을 벡터로 처리할 수 있는 np.where 함수를 갖추고 있습니다.

x = np.where(<조건>, <참일때 값>, <거짓일 때 값>)

<조건>은 일반적으로 파이썬 배열이 비교가 되고 각 원소에 대해서 원소가 참일 때 는 x에 <참일 때 값>이 들어가고 거짓일 때는 <거짓일 떄 값>이 들어가게 됩니다.

In [32]: x = np.array([-1, 0, 1])
   ....: y = np.where(x < 0, -1000, 1000)
   ....: y
   ....: 
Out[32]: array([-1000,  1000,  1000])

넘파이 배열의 인덱싱은 boolean 인덱싱이 가능합니다. 즉, 논리형 배열이 인덱스로 들어가면 True인 원소만 배열로 반환됩니다.

In [33]: a = np.arange(0, 11, 2.5)
   ....: a
   ....: 
Out[33]: array([ 0. ,  2.5,  5. ,  7.5, 10. ])

In [34]: b = a > 5
   ....: b
   ....: 
Out[34]: array([False, False, False,  True,  True])

In [35]: a[b]
Out[35]: array([ 7.5, 10. ])

Hat 함수

\[\begin{split}N(x) = \begin{cases} 0, & x <0 \\ x, & 0 \le x < 1 \\ 2 - x, & 1 \le x < 2 \\ 0, & x \ge 2 \\ \end{cases}\end{split}\]

파이썬 함수로는 다음과 같이 쓸 수 있습니다.

def N(x):
  if x < 0:
    return 0.0
  elif 0 <= x < 1:
    return x
  elif 1 <= x < 2:
    return 2 - x
  elif x >= 2:
    return 0.0

하지만 이 함수는 넘파이 배열과는 작동하지 않습니다. np.where를 사용하여 작성하면 다음과 같이 시도하려고 할 수 있습니다.

def Nv(x):
  r = np.where(x < 0, 0.0, 0.0)
  r = np.where(0 <= x < 1, x, r)
  r = np.where(1 <= x < 2, 2-x, r)
  r = np.where(x >= 2, 0.0, r)
  return r

하지만 여기서 파이썬 배열 비교 0 <= x < 1는 성립하지 않습니다. 이것을 가능하게 하기위해서는 logical_and 또는 logical_or를 사용하면 됩니다.

In [36]: def Nv1(x):
   ....:   condition1 = x < 0
   ....:   condition2 = np.logical_and(0 <= x, x < 1)
   ....:   condition3 = np.logical_and(1 <= x, x < 2)
   ....:   condition4 = x >= 2
   ....: 
   ....:   r = np.where(condition1, 0.0, 0.0)
   ....:   r = np.where(condition2, x, r)
   ....:   r = np.where(condition3, 2-x, r)
   ....:   r = np.where(condition4, 0.0, r)
   ....:   return r
   ....: 

다른 형태의 코드는 다음과 같습니다.

In [37]: def Nv2(x):
   ....:   condition1 = x < 0
   ....:   condition2 = np.logical_and(0 <= x, x < 1)
   ....:   condition3 = np.logical_and(1 <= x, x < 2)
   ....:   condition4 = x >= 2
   ....: 
   ....:   r = np.zeros_like(x)
   ....:   r[condition1] = 0.0
   ....:   r[condition2] = x[condition2]
   ....:   r[condition3] = 2-x[condition3]
   ....:   r[condition4] = 0.0
   ....:   return r
   ....: 

고차원 배열

이차원 배열

섭씨 화씨 온도 순서쌍에 대한 중첩 리스트를 생각해봅니다.

In [38]: cDegs = [-30 + i * 10 for i in range(3)]
   ....: fDegs = [9 / 5 * C + 32 for C in cDegs]
   ....: table = [[C, F] for C, F in zip(cDegs, fDegs)]
   ....: table
   ....: 
Out[38]: [[-30, -22.0], [-20, -4.0], [-10, 14.0]]

이것을 넘파이 배열로 바꾸면 다음과 같이 2차원 배열이 생성됩니다.

In [39]: table2 = np.array(table)
   ....: table2
   ....: 
Out[39]: 
array([[-30., -22.],
       [-20.,  -4.],
       [-10.,  14.]])

2차원 배열의 접근은 다음과 같이 인덱스를 이용합니다.

In [40]: table2[1][0]
Out[40]: -20.0

또는 다음과 같이 할 수도 있습니다.

In [41]: table2[1, 0]
Out[41]: -20.0

넘파이 배열의 크기는 shape 속성을 이용해서 얻을 수 있습니다.

In [42]: table2.shape
Out[42]: (3, 2)

(행의 크기, 열의 크기)로 표시됩니다. 다음과 같이 슬라이싱을 이용해서 부분 배열을 얻을 수 있습니다.

In [43]: table2[:, 1] # 2열
Out[43]: array([-22.,  -4.,  14.])

2차원 배열은 reshape 함수를 이용해서 만들 수도 있습니다.

In [44]: t = np.arange(1, 31).reshape(5, 6)
   ....: t
   ....: 
Out[44]: 
array([[ 1,  2,  3,  4,  5,  6],
       [ 7,  8,  9, 10, 11, 12],
       [13, 14, 15, 16, 17, 18],
       [19, 20, 21, 22, 23, 24],
       [25, 26, 27, 28, 29, 30]])

또한 슬라이싱을 이용해 부분 배열을 만들 수도 있습니다. 슬라이싱을 이용해서 만들어진 배열은 뷰(view)라서 뷰의 내용을 수정하면 원래 배열의 내용도 같이 수정된다는 것을 명심해야합니다.

In [45]: v1 = t[1:-1:2, 2:]
   ....: v1
   ....: 
Out[45]: 
array([[ 9, 10, 11, 12],
       [21, 22, 23, 24]])

v1[0, 0] 성분은 t[1, 2] 성분이므로 v1[0, 0] 바꾸면 원래 배열 t[1, 2] 성분이 바뀌는 것을 알 수 있습니다.

In [46]: v1[0, 0] = 100
   ....: print(v1)
   ....: 
   ....: print(t)
   ....: 
[[100  10  11  12]
 [ 21  22  23  24]]
[[  1   2   3   4   5   6]
 [  7   8 100  10  11  12]
 [ 13  14  15  16  17  18]
 [ 19  20  21  22  23  24]
 [ 25  26  27  28  29  30]]

만약 원래 배열과 상관없는 복사된 배열을 만들고 싶으면 copy 메소드를 이용하면 됩니다.

In [47]: c1 = t.copy()
   ....: c1
   ....: 
Out[47]: 
array([[  1,   2,   3,   4,   5,   6],
       [  7,   8, 100,  10,  11,  12],
       [ 13,  14,  15,  16,  17,  18],
       [ 19,  20,  21,  22,  23,  24],
       [ 25,  26,  27,  28,  29,  30]])

그리고 c1의 (1, 2) 성분을 9로 다시 바꿔봅니다. 그렇지만 t의 (1, 2) 성분은 그대로 100 임을 알 수 있습니다.

In [48]: c1[1, 2] = 9
   ....: print(c1)
   ....: 
   ....: print(t)
   ....: 
[[ 1  2  3  4  5  6]
 [ 7  8  9 10 11 12]
 [13 14 15 16 17 18]
 [19 20 21 22 23 24]
 [25 26 27 28 29 30]]
[[  1   2   3   4   5   6]
 [  7   8 100  10  11  12]
 [ 13  14  15  16  17  18]
 [ 19  20  21  22  23  24]
 [ 25  26  27  28  29  30]]

boolean index를 이용해서 조건을 만족하는 값을 한꺼번에 변경할 수 있습니다.

In [49]: c1[c1 >= 15] = 0

행렬 연산

2차원 배열은 행렬 연산을 할 수 있습니다.

In [50]: a = np.arange(12).reshape(3, 4)
   ....: b = np.arange(8).reshape(2, 4)
   ....: print(a,'\n', b)
   ....: 
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]] 
 [[0 1 2 3]
 [4 5 6 7]]

전치행렬은 T 속성을 이용합니다.

In [51]: bT = b.T
   ....: bT
   ....: 
Out[51]: 
array([[0, 4],
       [1, 5],
       [2, 6],
       [3, 7]])

행렬의 곱은 dot 또는 np.matmul 또는 @ 기호를 사용할 수 있습니다.

In [52]: print(a.dot(bT))
   ....: print(np.matmul(a, bT))
   ....: print(a @ bT)
   ....: 
[[ 14  38]
 [ 38 126]
 [ 62 214]]
[[ 14  38]
 [ 38 126]
 [ 62 214]]
[[ 14  38]
 [ 38 126]
 [ 62 214]]

참고로 dot 함수는 넘파이 배열의 브로드캐스트라는 연산을 통해서 더 일반적인 곱을 할 수 있습니다.

eye 함수를 이용해서 항등행렬을 만들 수 있고 zeros, ones를 이용해서 영행렬 및 1로 이루어진 행렬들을 만들 수 있습니다.

In [53]: A = np.eye(3)
   ....: A
   ....: 
Out[53]: 
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

선형대수

역행렬, 행렬식, 고유값

np.linalg 모듈을 이용해서 역행렬, 행렬식, 고유값 등을 계산할 수 있습니다.

In [54]: A = np.array([[2, 0], [0, 5]], dtype='float')
   ....: A
   ....: 
Out[54]: 
array([[2., 0.],
       [0., 5.]])

inv 함수를 이용해서 역행렬을 구합니다.

In [55]: np.linalg.inv(A)
Out[55]: 
array([[0.5, 0. ],
       [0. , 0.2]])

det 함수를 이용해 행렬식을 구합니다.

In [56]: np.linalg.det(A)
Out[56]: 9.999999999999998

eig 함수를 이용해서 고유값(eigenvalues), 고유벡터(eigenvectors)를 구합니다.

In [57]: eig_val, eig_vec = np.linalg.eig(A)
   ....: print(eig_val, '\n', eig_vec)
   ....: 
[2. 5.] 
 [[1. 0.]
 [0. 1.]]

외적, 노름, 합

크기 3인 벡터의 외적(cross product)은 cross 함수를 이용합니다.

In [58]: np.cross([1, 1, 1], [0, 0, 1])
Out[58]: array([ 1, -1,  0])

배열의 norm은 linalg.norm을 이용합니다.

In [59]: a = np.array([1, 1, 1])
   ....: b = np.array([0, 0, 1])
   ....: np.linalg.norm(a) # L2 norm
   ....: 
Out[59]: 1.7320508075688772

행렬의 각 축의 합은 sum 함수를 이용합니다.

In [60]: A
Out[60]: 
array([[2., 0.],
       [0., 5.]])

0축으로 합이란 0축으로 변하면서 합을 구하는 것입니다.

In [61]: A.sum(axis=0)
Out[61]: array([2., 5.])

최대, 최소는 max, min 함수를 이용합니다.

In [62]: np.max(A) # 전체의 최대값
   ....: A.max()
   ....: 
Out[62]: 5.0

축에 대해서 최대, 최소를 구합니다.

In [63]: A.max(axis=1)
Out[63]: array([2., 5.])

상삼각행렬, 하삼각행렬은 np.triu, np.tril를 이용합니다.

In [64]: B = np.array([[1, 2], [3, -4]])
   ....: print(np.triu(B))
   ....: print(np.tril(B))
   ....: 
[[ 1  2]
 [ 0 -4]]
[[ 1  0]
 [ 3 -4]]

연립방정식의 해

In [65]: A = np.array([[1, 2], [-2, 2.5]])
   ....: x = np.array([-1, 1])
   ....: b = np.dot(A, x)
   ....: 

np.linalg.solve를 이용해서 \(A x = b\)의 해를 구할 수 있습니다.

In [66]: np.linalg.solve(A, b)
Out[66]: array([-1.,  1.])

벡터장 및 3차원 플롯

\[f(x, y) = x^2 + y^2\]

3차원 플롯 준비 ~~~~~~~~~~~~~~~~`

from mpl_toolkits.mplot3d import Axes3D를 이용해 3차원 플롯을 할 수 있도록 설정을 하고 projection='3d' 옵션을 이용해 3차원 플롯을 합니다.

In [67]: from mpl_toolkits.mplot3d import Axes3D
   ....: import matplotlib.pyplot as plt
   ....: 
   ....: fig = plt.figure()
   ....: ax = fig.add_subplot(111, projection='3d')
   ....: 

라인 플롯

매개변수 함수는 plot 함수를 이용합니다.

In [68]: theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
   ....: z = np.linspace(-2, 2, 100)
   ....: x = np.sin(theta)
   ....: y = np.cos(theta)
   ....: ax.plot(x, y, z, label='parametric curve')
   ....: ax.legend()
   ....: 
Out[68]: <matplotlib.legend.Legend at 0x1f0f17dc2e8>

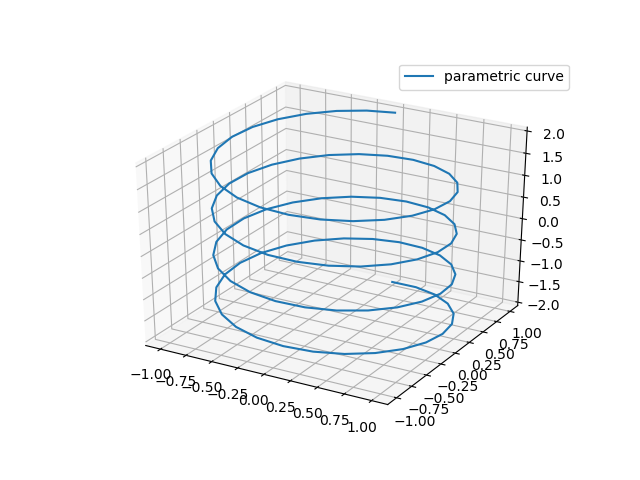
meshgrid

3차원 플롯은 2차원 평면의 격자점에서 함수값을 계산해서 함수값을 연결해서 보여줍니다.

그러므로 2차원 좌표평면을 x, y 격자점으로 나타낼 필요가 있습니다. 이러한 것을 해주는 것이 meshgrid 함수 입니다.

In [69]: x = np.arange(-2, 3)
   ....: y = np.arange(-2, 3)
   ....: 
   ....: xx, yy = np.meshgrid(x, y)
   ....: print(xx, '\n', yy)
   ....: 
[[-2 -1  0  1  2]
 [-2 -1  0  1  2]
 [-2 -1  0  1  2]
 [-2 -1  0  1  2]
 [-2 -1  0  1  2]] 
 [[-2 -2 -2 -2 -2]
 [-1 -1 -1 -1 -1]
 [ 0  0  0  0  0]
 [ 1  1  1  1  1]
 [ 2  2  2  2  2]]

따라서 \(z = x^2 + y^2\) 값을 계산하기 위해서는 다음과 같이 해야합니다.

In [70]: zz = xx ** 2 + yy ** 2
   ....: zz
   ....: 
Out[70]: 
array([[8, 5, 4, 5, 8],
       [5, 2, 1, 2, 5],
       [4, 1, 0, 1, 4],
       [5, 2, 1, 2, 5],
       [8, 5, 4, 5, 8]], dtype=int32)

wireframe 플롯

plot_wireframe 함수를 이용하여 플롯을 합니다.

In [71]: x = np.linspace(-10, 10, 101)
   ....: y = np.linspace(-10, 10, 101)
   ....: xx, yy = np.meshgrid(x, y)
   ....: zz = xx ** 2 + yy ** 2
   ....: ax.plot_wireframe(xx, yy, zz)
   ....: 
Out[71]: <mpl_toolkits.mplot3d.art3d.Line3DCollection at 0x1f0f17ee208>

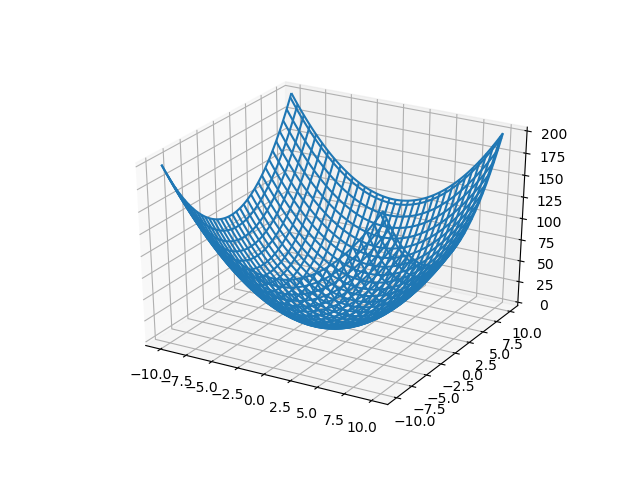
surface 플롯

plot_surface 함수를 이용하여 플롯을 합니다.

In [72]: x = np.linspace(-10, 10, 101)
   ....: y = np.linspace(-10, 10, 101)
   ....: xx, yy = np.meshgrid(x, y)
   ....: zz = xx ** 2 + yy ** 2
   ....: ax.plot_surface(xx, yy, zz)
   ....: 
Out[72]: <mpl_toolkits.mplot3d.art3d.Poly3DCollection at 0x1f0f1945be0>

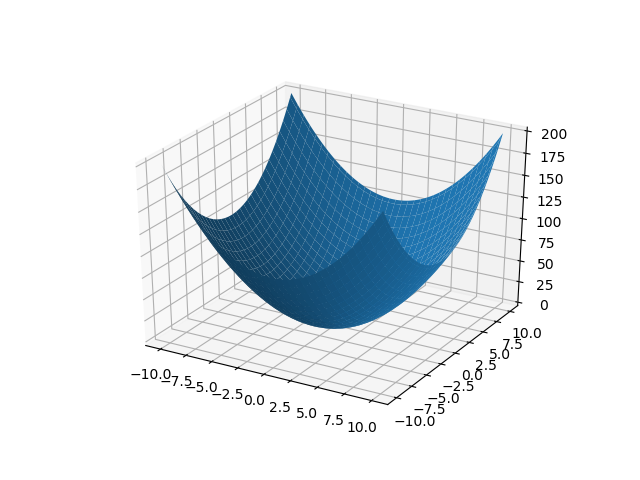
scatter 플롯

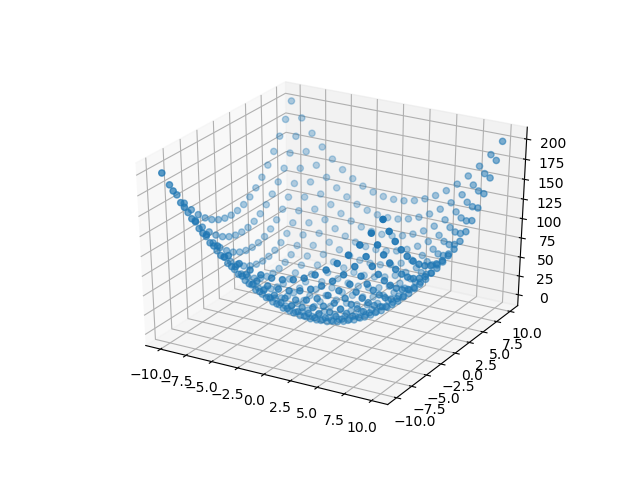
scatter 함수를 이용하여 플롯을 합니다.

In [73]: xs = np.linspace(-10, 10, 21)
   ....: ys = np.linspace(-10, 10, 21)
   ....: xxs, yys = np.meshgrid(xs, ys)
   ....: zzs = xxs ** 2 + yys ** 2
   ....: ax.scatter(xxs, yys, zzs)
   ....: 
Out[73]: <mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x1f0f17b9588>

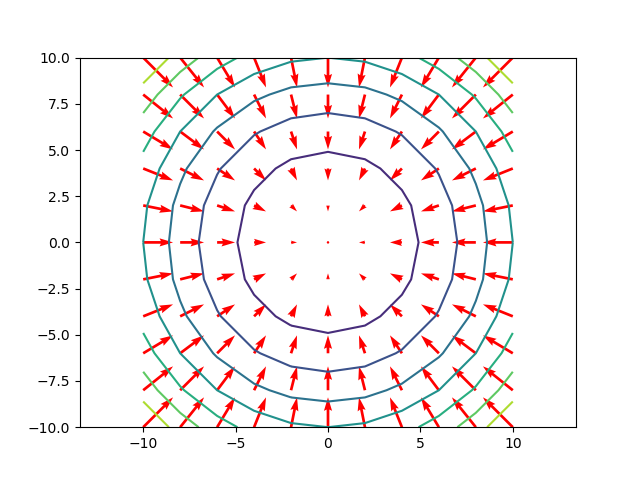
벡터장

그래디언트 \(\nabla f\)

\[\nabla f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)\]

In [74]: fig = plt.figure()
   ....: ax = fig.add_subplot(111)
   ....: 

In [75]: x2 = y2 = np.linspace(-10., 10., 11)
   ....: xx2, yy2 = np.meshgrid(x2, y2)
   ....: zz2 = xx2 ** 2 + yy2 ** 2 # h on coarse grid
   ....: dhdx, dhdy = 2 * xx2, 2 * yy2
   ....: ax.quiver(xx2, yy2, -dhdx, -dhdy, color='r', angles='xy')
   ....: ax.set_xlim([-10, 10])
   ....: ax.set_ylim([-10, 10])
   ....: ax.contour(xx2, yy2, zz2)
   ....: ax.axis('equal')
   ....: 
Out[75]: (-10.0, 10.0, -10.0, 10.0)

연습문제

1. 함수

   \[h(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x^2}\]

   에 대해서 구간 [-4, 4]를 41 개의 균등 분할 점들을 xlist 와 거기에 대응하는 함수 \(h(x)\) 값들에 대한 hlist를 구하시오.

2. 1번 문제에서 주어진 함수 \(h(x)\)를 이용하여 두 개의 넘파이 배열 x, y를 만드세요. 우선 빈 배열 x, y를 만들고 for 문을 이용하여 x, y의 원소를 채우세요.

3. 2번 문제에서 x, y를 구할 때 np.linspace 함수를 이용하여 넘파이 배열 x를 구하고 y 값을 구할 때도 벡터함수 처리를 하여 구하세요.

4. 1번 함수 \(h(x)\)의 그래프를 [-4, 4] 범위에서 그리세요.

5. 벡터 \(v = (2, 3, -1)\)와 함수 \(f(x) = x^3 + xe^x +1\)에 대해서 벡터함수 값 \(f(v)\)를 구할 때 벡터 연산 규칙 v ** 3 + v * exp(v) + 1을 손으로 계산해보고 파이썬으로 계산해서 같은지를 확인하세요.

6. x, t는 크기가 같은 배열이라고 가정할 때 다음 벡터식

   y = cos(sin(x)) + exp(1/t)
   

   의 값을 손으로 계산하세요. x는 0, 2를 원소로 갖고 t는 1, 1.5를 원소로 가질 때 값을 구하세요. 계산 결과를 넘파이를 이용해서 계산한 결과와 비교해보세요.

7. 0, 0.1, 0.2, \(\ldots\), 3으로 이루어진 넘파이 배열 w를 만들 때, w[:], w[:-2], w[::5]가 의미하는 것을 말하세요.

8. \(v_0 = 10\), \(g = 9.8\) 일 때 \(y(t) = v_0 t - \frac{1}{2}gt^2\)에 대한 함수의 그래프를 \(t \in [0, 2v_0/g]\) 범위에서 그리세요. 축 레이블을 각각 time(s) 및 height(m)와 같이 표시하세요.

9. 위 8번 문제에서 \(v_0\)를 사용자로부터 입력받아 그래프를 그리는 프로그램을 작성하세요.

10. 공의 궤적에 대한 함수는 다음과 같습니다.

    \[f(x) = x \tan \theta - \frac{1}{2v_0^2}\frac{gx^2}{\cos^2\theta} + y_0\]

    \(x\)는 지상에서의 거리, \(g\)는 중력가속도, \(v_0\)는 초속도, \(\theta\)는 지면과 이루는 각도, \(y_0\)는 처음 높이를 의미합니다.

    사용자로부터 \(y_0\), \(\theta\), \(v_0\)를 입력받아 궤적 \(y = f(x)\)를 그리는 프로그램을 작성하세요. \(g=9.8\)로 놓고 계산하세요.

연습문제 풀이