신경망 학습

학습이란 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것을 말합니다. 앞장에서는 미리 만들어진 가중치 매개변수를 이용하여 새로운 데이터에 대한 추론을 하는 방법에 대해서 알아봤습니다. 이번 장에서는 주어진 데이터를 이용하여 참값이 되도록 훈련을 하여 최적의 참값이 나오도록 가중치 매개변수를 구하는 방법(학습)에 대해서 알아봅니다.

데이터

기계학습 문제를 풀 때는 데이터를 훈련데이터(training data)와 시험데이터(test data)로 나눠 학습과 시험을 수행합니다. 먼저 훈련데이터를 이용하여 최적의 매개변수를 찾습니다. 다음으로 시험데이터를 이용하여 훈련데이터를 통하여 얻어진 매개변수가 얼마나 잘 맞는지를 시험합니다. 두 개의 데이터셋으로 나누는 이유는 일반적으로 훈련데이터를 통하여 만들어진 매개변수는 훈련데이터에는 잘 맞기 때문에 훈련데이터로 다시 평가를 하는 것은 올바르지 않을 수 있습니다. 따라서 훈련데이터 밖에 있는 데이터 즉, 시험데이터를 가지고 만들어진 매개변수가 잘 맞는지를 평가합니다.

참고로 한 데이터셋에만 지나치게 최적화된 상태를 과대적합(overfitting)이라고 합니다.

손실함수(loss function)

훈련을 통해 찾은 매개변수가 실제로 얼마나 오차가 많은지를 측정하는 함수가 손실함수(loss function or cost function)입니다.

평균제곱오차(mean squared error, MSE)

\[E = \frac{1}{2} \sum_{k=1}^M (y_k - t_k)^2\]

$y_k$는 신경망의 출력이고 $t_k$는 정답 레이블 $M$은 출력 데이터의 차원을 의미합니다. 예를 들어 손글씨 숫자 인식에서 출력데이터의 차원은 $0, 1, \ldots, 9$ 까지 $M=10$이 됩니다.

파이썬 예를 들면 t가 실제 숫자 레이블에 해당되는 배열로 1이 레이블 숫자에 해당하는 것을 의미합니다. 아래에서는 레이블이 숫자 2에 해당되는 겁니다.

In [1]: import numpy as np
   ...: y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
   ...: t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
   ...: 

y는 소프트맥스 함수의 출력으로 가정한다면 각 숫자에 대응되는 확률로 생각할 수 있습니다. 2에 대응되는 수 0.6이 가장 큰 확률을 보이므로 적절히 추정을 했다고 볼 수 있습니다.

위에서 정의한 평균제곱오차는 다음과 같이 넘파이로 정의할 수 있습니다.

In [2]: def mean_squared_error(y, t):
   ...:   return 0.5 * np.sum((y - t) ** 2)
   ...: 

위에서 정의한 y, t에 대해서 오차를 계산하면 0.098 정도로 낮은 손실을 보이는 것을 알 수 있습니다.

In [3]: mean_squared_error(y, t)
Out[3]: 0.09750000000000003

만일 7 이라고 예측을 했을 때를 계산하면 다음과 같이 0.598 정도로 높은 손실을 출력하는 것을 알 수 있습니다.

In [4]: y1 = np.array([0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0])
   ...: mean_squared_error(y1, t)
   ...: 
Out[4]: 0.5975

교차엔트로피 오차

교차엔트로피 오차(cross entroy error)는 다음과 같이 정의합니다. 엔트로피와 교차엔트로피는 이곳을 참조바랍니다.

\[E = - \sum_{k=1}^M t_k \log y_k\]

평균제곱오차와 마찬가지로 $y_k$는 신경망의 출력이고 $t_k$는 정답 레이블, $M$은 출력 데이터의 차원을 의미합니다.

In [5]: def cross_entropy_error(y, t):
   ...:   delta = 1e-7
   ...:   return -np.sum(t * np.log(y + delta))
   ...: 

delta를 더하는 이유는 분모가 0이되서 -inf가 되는 것을 막기위한 것입니다.

y는 정답일 때 예측값이고 y1은 오답일 때의 예측값입니다. 다음과 같이 y1일 때 오차가 크게 나오는 것을 알 수 있습니다.

In [6]: import numpy as np
   ...: y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
   ...: t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
   ...: 
   ...: print(cross_entropy_error(y, t))
   ...: 
   ...: y1 = np.array([0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0])
   ...: print(cross_entropy_error(y1, t))
   ...: 
0.510825457099338
2.302584092994546

미니배치 학습

훈련데이터를 가지고 학습을 할 때 훈련데이터의 평균 손실함수를 구합니다.

\[E = - \frac{1}{N}\sum_{n=1}^N\sum_{k=1}^M t_{nk} \log y_{nk}\]

여기서 데이터의 갯수는 N이고 각각의 데이터에 대한 손실함수를 합하여 평균을 낸 것입니다.

MNIST 데이터셋은 6만개였습니다. 따라서 모든 데이터를 대상으로 손실함수의 합을 계산하는 것은 시간이 걸립니다. 더 나아가 빅데이터 수준의 데이터의 크기는 수백만에서 수천만에 이르기 때문에 전체를 대상으로 손실함수를 계산하는 것은 현실적인 어려움에 부딪칩니다. 이런 경우 전체의 일부만 골라서 학습을하여 근사치를 사용할 수 있습니다. 이러한 방법을 미니배치(mini-batch) 학습이라고 합니다.

다음과 같이 MNIST 데이터셋으로부터 손글씨 자료를 읽어옵니다. one_hot_label=True로 설정하여 원핫인코딩인 배열로 읽어옵니다. 각 레이블은 정답에 해당하는 값만 1이고 나머지는 0인 10 개의 원소를 갖는 배열로 이루어집니다.

In [7]: import sys, os
   ...: sys.path.append(os.path.join(os.getcwd(), 'src'))
   ...: from dataset.mnist import load_mnist
   ...: 
   ...: (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
   ...: print('훈련데이터 크기: ', x_train.shape)
   ...: print('레이블의 크기: ', t_train.shape)
   ...: 
훈련데이터 크기:  (60000, 784)
레이블의 크기:  (60000, 10)

여기서 무작위로 10개의 데이터만 뽑으려면 np.random.choice 함수를 사용하면 됩니다. 다음은 6만개(0부터 59999까지) 중에서 10개의 수를 임의로 뽑아냅니다.

In [8]: np.random.choice(60000, 10)
Out[8]: 
array([22474, 18545,  9436, 52139,  3781,  6916, 42255,  9163, 40071,
       35496])

훈련데이터 중에서 원하는 인덱스에 해당하는 원소만을 갖는 배열을 뽑으려면 배열에 인덱스 배열값을 인자로 넘겨주면 됩니다.

In [9]: train_size = x_train.shape[0]
   ...: batch_size = 10
   ...: batch_mask = np.random.choice(train_size, batch_size)
   ...: x_batch = x_train[batch_mask]
   ...: t_batch = t_train[batch_mask]
   ...: 

배치 교차엔트로피 오차 구현

In [10]: def cross_entropy_error(y, t):
   ....:   delta = 1e-7
   ....:   if y.ndim == 1:
   ....:     t = t.reshape(1, t.size)
   ....:     y = y.reshape(1, y.size)
   ....:   batch_size = y.shape[0]
   ....:   return -np.sum(t * np.log(y + delta)) / batch_size
   ....: 

t, y가 1차원 배열이면 reshape 함수를 이용해서 2차원 배열로 바꿔줍니다.

다음은 one_hot_label 옵션을 이용하여 원핫인코딩일 때와 그렇지않고 숫자 레이블로 주어졌을 때 동시에 처리할 수 있도록합니다.

In [11]: def cross_entropy_error(y, t):
   ....:   if y.ndim == 1:
   ....:     t = t.reshape(1, t.size)
   ....:     y = y.reshape(1, y.size)
   ....: 
   ....:   # 원-핫 벡터이면 정답 레이블의 인덱스로 변경
   ....:   if t.size == y.size:
   ....:     t = t.argmax(axis=1)
   ....: 
   ....:   batch_size = y.shape[0]
   ....:   return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
   ....: 

신경망 학습에서는 최적의 매개변수를 찾기위해서 손실함수의 값을 가능한 작게 하도록 하는 매개변수를 찾습니다. 미분을 이용합니다.

위의 함수를 common 폴더에 functions.py 파일 안에 저장합니다.

수치 미분

미분

\[\frac{df(x)}{dx} = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\]

다음은 정의 그대로 파이썬으로 구현한 것입니다. $h$를 더 작게 잡으면 더 정확하게 나올 것이라고 생각하기 쉬운데 컴퓨터 정밀도(precision)의 한계로 원하는 결과가 나오지 않을 수 있습니다.

In [12]: def numerical_diff(f, x):
   ....:   h = 1e-50
   ....:   return (f(x + h) - f(x)) / h
   ....: 

h가 파이썬에서 허용하는 정밀도의 한계를 넘어서 1e-50에 1을 더해도 1이라고 계산을 하므로 위의 결과값은 항상 0이되는 것을 알 수 있습니다. 따라서 정당히 작은 h=1e-4를 선택하도록 하겠습니다.

수치적으로 미분하는 방법으로 여러 가지가 있지만 그 중에서 중앙차분(central difference)이 일반적으로 더 정확히 계산하므로 이 방법을 사용하도록 합니다. 위의

In [13]: def numerical_diff(f, x):
   ....:   h = 1e-4
   ....:   return (f(x + h) - f(x-h)) / (2 * h)
   ....: 

예를 들어봅니다.

In [14]: def f1(x):
   ....:   return 0.01 * x ** 2 + 0.1 * x
   ....: 
   ....: numerical_diff(f1, 5)
   ....: 
Out[14]: 0.1999999999990898

편미분

편미분은 다변수 함수에서 하나의 변수에 대해서 미분을 하는 것을 말합니다.

\[\begin{split}\frac{\partial f}{\partial x}(x_0, y_0) &= \lim_{h \to 0} \frac{f(x_0+h, y_0) - f(x_0, y_0)}{h} \\ \frac{\partial f}{\partial y}(x_0, y_0) &= \lim_{h \to 0} \frac{f(x_0, y_0+h) - f(x_0, y_0)}{h} \\\end{split}\]

다음과 같은 함수를 예로 들어봅니다.

\[f(x, y) = x^2 + y^2\]

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

f2 = lambda x, y: x ** 2 + y ** 2

x = np.linspace(-3, 3, 21)
y = np.linspace(-3, 3, 21)
xx, yy = np.meshgrid(x, y)
zz = f2(xx, yy)

ax.plot_wireframe(xx, yy, zz)

(Source code, png, hires.png, pdf)

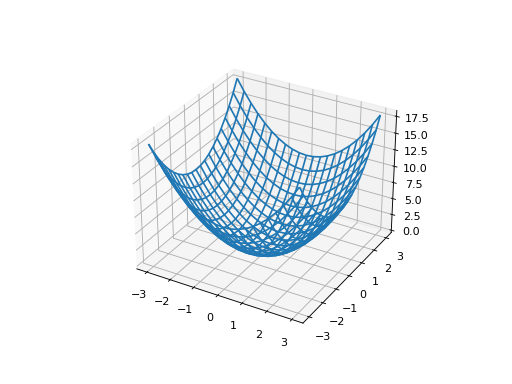
그래디언트(gradient)

다변수 함수 $f(x_1, x_2, \ldots, x_n)$의 각각에 대한 편미분 벡터를 그래디언트라고 합니다.

\[\nabla f(x_1, x_2, \ldots, x_n) = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n}\right)\]

다음과 같이 수치 그래디언트 함수를 작성합니다. 이 함수는 함수 f와 x를 인자로 갖는데 함수는 넘파이 배열 x를 인자로 갖습니다.

In [15]: def numerical_grad_1d(f, x):
   ....:   h = 1e-4
   ....:   grad = np.zeros_like(x)
   ....: 
   ....:   for idx in range(x.size):
   ....:     tmp = x[idx]
   ....:     x[idx] = tmp + h
   ....:     fx1 = f(x)
   ....:     x[idx] = tmp - h
   ....:     fx2 = f(x)
   ....:     grad[idx] = (fx1 - fx2) / (2 * h)
   ....:     x[idx] = tmp
   ....:   return grad
   ....: 

함수 $f(x, y) = x^2 + y^2$를 정의하면 다음과 같이 할 수 있습니다. x0= [1, 1] 일 때 그래디언트를 계산해보면 다음과 같은 결과가 나옵니다.

In [16]: def f3(x):
   ....:   return np.sum(x ** 2)
   ....: 
   ....: x0 = np.array([1, 1])
   ....: grad_f3 = numerical_grad_1d(f3, x0)
   ....: print(grad_f3)
   ....: 
[5000 5000]

정확한 값은 [2, 2]가 맞는데 [5000, 5000]이 나왔습니다. 이것은 넘파이 배열이 데이터형으로 계산되기 때문입니다. 즉, x0 넘파이 배열을 만들 때 [1, 1] 이라고 했기 때문에 기본적으로 np.int32 형으로 만듭니다. 이렇게 되면 x0의 모든 값은 정수형으로 바뀌어 저장이 됩니다.

예를 들어보겠습니다. 위에서 정의한 데이터형을 출력해봅니다.

In [17]: x0.dtype
Out[17]: dtype('int32')

int32 형인 것을 알 수 있습니다. x0의 원소를 다음과 같이 실수형으로 입력해봅니다. 하지만 출력되는 것은 정수형으로 바뀌어 저장된 것을 알 수 있습니다.

In [18]: x0[0] = 100.234
   ....: print(x0[0])
   ....: 
100

따라서 위 함수 numerical_grad의 인자를 넘겨줄 때 올바른 타입을 넘겨주도록 해야합니다.

In [19]: x0 = np.array([1., 1.])
   ....: grad_f3 = numerical_grad_1d(f3, x0)
   ....: print(grad_f3)
   ....: 
[2. 2.]

2차원 배열 입력에 계산되도록 그래디언트 함수를 수정합니다.

In [20]: def numerical_grad_2d(f, X):
   ....: 
   ....:   if X.ndim == 1:
   ....:     return numerical_grad_1d(f, X)
   ....:   else:
   ....:     grad = np.zeros_like(X)
   ....:     for idx, x in enumerate(X):
   ....:       grad[idx] = numerical_grad_1d(f, x)
   ....:     return grad
   ....: 

또한 함수 $f(x, y) = x^2 + y^2$도 2차원 배열에 대해서 작동하도록 변경합니다. (x, y) 순서쌍 배열을 갖습니다.

In [21]: def f(x):
   ....:   if x.ndim == 1:
   ....:     s = np.sum(x ** 2)
   ....:   else:
   ....:     s = np.sum(x ** 2, axis=1)
   ....:   return s
   ....: 
   ....: x = np.linspace(-3, 3, 7)
   ....: y = np.linspace(-3, 3, 7)
   ....: xy = np.array([x, y]).T
   ....: 
   ....: print(f(np.array([1., 2.])))
   ....: print(f(xy))
   ....: 
5.0
[18.  8.  2.  0.  2.  8. 18.]

그래디언트 함수를 테스트해봅니다.

In [22]: numerical_grad_2d(f, xy)
Out[22]: 
array([[-6., -6.],
       [-4., -4.],
       [-2., -2.],
       [ 0.,  0.],
       [ 2.,  2.],
       [ 4.,  4.],
       [ 6.,  6.]])

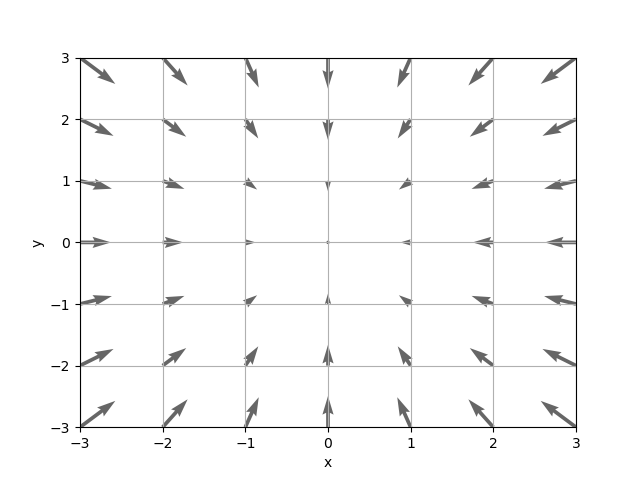
다음은 -3부터 3까지 각 격자점에서 그래디언트를 구해서 벡터장으로 표현해본 것입니다. 그래디언트의 음의 방향을 표시한겁니다.

In [23]: xx, yy = np.meshgrid(x, y)
   ....: xflat = xx.flatten()
   ....: yflat = yy.flatten()
   ....: xyflat = np.array([xflat, yflat]).T
   ....: grad = numerical_grad_2d(f, xyflat).T
   ....: 
   ....: plt.figure()
   ....: plt.quiver(xflat, yflat, -grad[0], -grad[1], angles="xy", color="#666666")
   ....: plt.xlim([-3, 3])
   ....: plt.ylim([-3, 3])
   ....: plt.xlabel('x')
   ....: plt.ylabel('y')
   ....: plt.grid()
   ....: 

실제로 그래디언트를 계산할 때는 다음과 같은 좀 더 효율적인 코드를 사용하도록 합니다.

def numerical_gradient(f, x):
  h = 1e-4
  grad = np.zeros_like(x)

  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:
    idx = it.multi_index
    tmp = x[idx]
    x[idx] = tmp + h
    fx1 = f(x)
    x[idx] = tmp - h
    fx2 = f(x)
    grad[idx] = (fx1 - fx2) / (2 * h)
    x[idx] = tmp
    it.iternext()
  return grad

np.nditer(x)는 x 배열의 순환 객체를 반환합니다. nditer.finished는 순환이 끝나면 True 그렇지 않으면 False를 반환합니다. nditer.iternext() 메소드는 다음 성분으로 이동을 합니다. op_flags=['readwrite'] 옵션을 이용해서 배열의 원소들을 변경할 수 있도록합니다. 기본 설정값은 readonly 입니다. flags=['multi_index'] 옵션을 이용해 다중 인덱스를 불러올 수 있습니다. 불러올 때는 nditer.multi_index를 사용합니다.

경사하강법

신경망 학습시 최적의 매개변수(가중치와 편향)를 찾기 위해서 손실함수가 최소가 되도록 합니다. 일반적으로 손실함수는 매우 복잡해서 최소값을 찾기 어렵습니다. 최소값을 찾는 방법 중의 하나가 어떤 지점에서 그래디언트를 이용해서 가장 빨리 감소하는 방향으로 찾아가는 방법이 경사하강법(gradient descent method)입니다.

어떤 점 $(x_0, x_1)$에서 가장 빨리 손실함수가 감소하는 방향이 그래디언트의 음의 방향입니다. 따라서 다음으로 이동할 점은 다음과 같이 구합니다.

\[\begin{split}x_0 = x_0 - \eta \frac{\partial f}{\partial x_0} \\ x_1 = x_1 - \eta \frac{\partial f}{\partial x_1}\end{split}\]

여기서 $\eta$는 학습률(learning rate)이라고 하며 사용자가 직접 지정해주어야 합니다. 이렇듯 사용자가 직접 지정해 주는 매개변수를 초매개변수(hyper parameter)라고 합니다.

In [24]: def gradient_descent(f, init_x, lr=0.01, step_num=100):
   ....:   x = init_x
   ....: 
   ....:   for i in range(step_num):
   ....:     grad = numerical_grad_2d(f, x)
   ....:     x -= lr * grad
   ....:   return x
   ....: 

위에서 정의한 함수에 대해서 경사하강법을 시험해봅니다.

In [25]: init_x = np.array([-3.0, 4.0])
   ....: gradient_descent(f, init_x, lr=0.1)
   ....: 
Out[25]: array([-6.11110793e-10,  8.14814391e-10])

In [26]: x = np.array([-3.0, 4.0])
   ....: 
   ....: lr = 0.1
   ....: x_trace = []
   ....: x_trace.append(x)
   ....: 
   ....: for i in range(100):
   ....:   grad = numerical_grad_2d(f, x)
   ....:   x = x - lr * grad
   ....:   x_trace.append(x)
   ....: 
   ....: xtrace = np.array(x_trace)
   ....: 
   ....: fig, ax = plt.subplots()
   ....: ax.plot( [-5, 5], [0,0], '--b')
   ....: ax.plot( [0,0], [-5, 5], '--b')
   ....: ax.plot(xtrace[:,0], xtrace[:,1], 'o')
   ....: c1 = plt.Circle((0, 0), 0.5, fill=False, linestyle='--')
   ....: c2 = plt.Circle((0, 0), 1, fill=False, linestyle='--')
   ....: c3 = plt.Circle((0, 0), 2, fill=False, linestyle='--')
   ....: c4 = plt.Circle((0, 0), 3, fill=False, linestyle='--')
   ....: c5 = plt.Circle((0, 0), 4, fill=False, linestyle='--')
   ....: 
   ....: ax.add_artist(c1)
   ....: ax.add_artist(c2)
   ....: ax.add_artist(c3)
   ....: ax.add_artist(c4)
   ....: ax.add_artist(c5)
   ....: ax.set_aspect('equal')
   ....: ax.set_xlim(-4.5, 4.5)
   ....: ax.set_ylim(-4.5, 4.5)
   ....: ax.set_xlabel("X0")
   ....: ax.set_ylabel("X1")
   ....: 
Out[26]: Text(0, 0.5, 'X1')

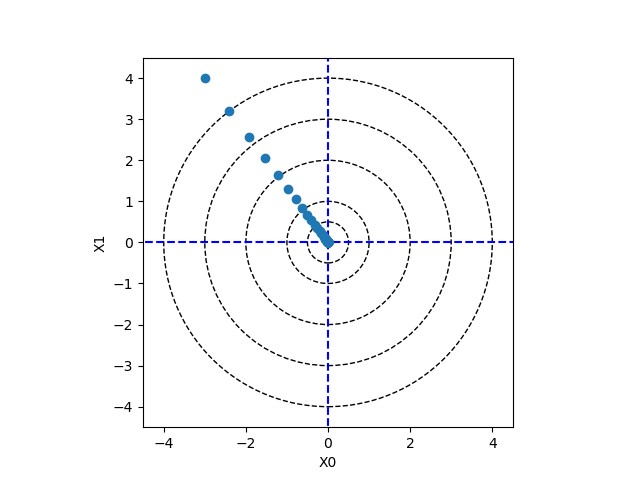
신경망 그래디언트

크기가 2x3 인 가중치 행렬 $\mathbf{W}$ 와 손실함수 $L$이 주어질 때 $\mathbf{W}$에 대한 $L$의 그래디언트는 다음과 같이 계산할 수 있습니다.

\[ \begin{align}\begin{aligned}\begin{split}\mathbf{W} = \left(\begin{array}{ccc} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ \end{array}\right)\end{split}\\\begin{split}\frac{\partial L}{\partial\mathbf{W}} = \left(\begin{array}{ccc} \frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{13}} \\ \frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{23}} \\ \end{array}\right)\end{split}\end{aligned}\end{align} \]

간단한 신경망을 이용하여 그래디언트를 구하는 코드 SimpleNet 클래스를 작성해봅니다.

In [27]: import sys
   ....: sys.path.append(os.path.join(os.getcwd(), 'src'))
   ....: import numpy as np
   ....: from common.functions import softmax, cross_entropy_error
   ....: from common.gradient import numerical_gradient
   ....: 
   ....: class SimpleNet:
   ....:   def __init__(self):
   ....:     np.random.seed(21)
   ....:     self.W = np.random.randn(2, 3)
   ....: 
   ....:   def predict(self, x):
   ....:     return np.dot(x, self.W)
   ....: 
   ....:   def loss(self, x, t):
   ....:     z = self.predict(x)
   ....:     y = softmax(z)
   ....:     loss = cross_entropy_error(y, t)
   ....:     return loss
   ....: 

In [28]: net = SimpleNet()
   ....: print(net.W)
   ....: 
[[-0.05196425 -0.11119605  1.0417968 ]
 [-1.25673929  0.74538768 -1.71105376]]

In [29]: x = np.array([0.6, 0.9])
   ....: p = net.predict(x)
   ....: print(p)
   ....: 
   ....: np.argmax(p)
   ....: 
[-1.16224391  0.60413128 -0.91487031]
Out[29]: 1

In [30]: t = np.array([0, 0, 1])
   ....: net.loss(x, t)
   ....: 
Out[30]: 1.8482197280551642

In [31]: def f(W):
   ....:   return net.loss(x, t)
   ....: 
   ....: dW = numerical_gradient(f, net.W)
   ....: print(dW)
   ....: 
[[ 0.07379825  0.43169108 -0.50548933]
 [ 0.11069738  0.64753662 -0.758234  ]]

numerical_gradient(f, W)가 계산되는 과정을 살펴봅니다. 인자로 건네지는 함수 f는 W와 상관없이 loss(x, t) 값이 반환됩니다. 즉, 인자 W는 더미(dummy) 변수로 아무런 역할도 하지 않습니다. 그런데 net.loss(x, t) 함수 호출을 보면 x, t는 고정되어 있어서 항상 같은 값이 반환될 것 같지만 그렇지 않은 것을 알 수 있습니다.

그 이유는 numerical_gradient 함수 내에서 f(x)를 호출하는 과정에서 x의 값이 변경됩니다. 여기서 x는 net.W를 의미합니다. W 값이 변경된 상태에서 net.loss 함수를 호출하게 되면 loss 함수는 다시 predict 함수를 호출합니다. 이때 predict 함수는 x와 W를 사용하여 계산을 하게 되므로 numerical_gradient에서 변경된 W가 적용이되어 다른 값이 나오게 됩니다.

predict 에서 변경된 값은 cross_entropy_error를 계산할 때 적용이되어 loss 함수의 값이 바뀌게 되어 결국에는 f(x)가 호출될 때마다 함수값이 변경된 값이 반환되게 되는 것입니다.

디버깅

VS Code(Visual Studio Code)에서 파이썬 코드 디버깅에 대해서 알아봅니다.

vscode 왼쪽에 있는 디버깅 탭을 누릅니다.
기어 아이콘을 눌러 launch.json 파일을 만듭니다. 자동으로 여러 가지 실행 방법이 설정이되는 것을 알 수 있습니다.
다음은 launch.json 파일 예제입니다. 여기서 "cwd": "${fileDirname}"를 특별히 추가해주면 실행 파일 디렉토리를 기준으로 패키지를 상대적으로 불러올 수 있습니다.

{
    // IntelliSense를 사용하여 가능한 특성에 대해 알아보세요.
    // 기존 특성에 대한 설명을 보려면 가리킵니다.
    // 자세한 내용을 보려면 https://go.microsoft.com/fwlink/?linkid=830387을(를) 방문하세요.
    "version": "0.2.0",
    "configurations": [
        {
            "name": "Python: Current File",
            "type": "python",
            "request": "launch",
            "program": "${file}",
            "console": "integratedTerminal",
            "cwd": "${fileDirname}"
        }
    ]
}

파이썬 코드 파일을 열고 왼쪽 부분에 마우스를 올려 놓으면 빨간색 표시가 나오면 클릭하여 중단점(break point)을 설정합니다. 디버그 초록색 버튼을 누르면 중단점에서 프로그램이 멈추어 있는 것을 알 수 있습니다.

학습 알고리즘 구현

1단계 - 미니배치: 훈련데이터 중 무작위로 일부를 가져옵니다.
2단계 - 그래디언트 산출: 가중치 매개변수의 그래디언트를 구합니다.
3단계 - 매개변수 갱신: 가중치 매개변수를 갱신합니다.
4단계 - 반복: 1-3단계를 반복합니다.

2층 신경망 클래스 구현

ch04/two_layer_net.py

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 부모 디렉터리의 파일을 가져올 수 있도록 설정
from common.functions import *
from common.gradient import numerical_gradient


class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 가중치 초기화
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
    
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)
        
        return y
        
    # x : 입력 데이터, t : 정답 레이블
    def loss(self, x, t):
        y = self.predict(x)
        
        return cross_entropy_error(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
        
    # x : 입력 데이터, t : 정답 레이블
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads
        
    def gradient(self, x, t):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        grads = {}
        
        batch_num = x.shape[0]
        
        # forward
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)
        
        # backward
        dy = (y - t) / batch_num
        grads['W2'] = np.dot(z1.T, dy)
        grads['b2'] = np.sum(dy, axis=0)
        
        da1 = np.dot(dy, W2.T)
        dz1 = sigmoid_grad(a1) * da1
        grads['W1'] = np.dot(x.T, dz1)
        grads['b1'] = np.sum(dz1, axis=0)

        return grads

__init__ 함수를 통해서 W, b를 주어진 크기의 무작위 값으로 초기화합니다. 주어진 x, t 값에 대한 numerical_gradient를 구합니다. 그래디언트를 구할 때 인자로 loss_W, self.params 들이 전달됩니다. loss_W는 인자 W와는 상관없이 self.loss(x, t) 값을 반환합니다. 즉, W는 더미 ^dummy 변수입니다. self.loss가 반환하는 값은 교차엔트로피 오차를 반환하게 됩니다.

numerical_gradient 함수 내부를 살펴보면 f(x)를 계산하는 과정이 있는데 이것이 실행될 때마다 self.loss 함수가 실행이 되는 것입니다. 겉으로 보기에는 self.loss(x, t)는 x, t가 변하지 않기 때문에 상수값이 반환될 것이라고 생각할 수 있지만 실제로는 numerical_gradient 함수 내부에서 W 값의 성분들이 변하기 때문에 self.loss 값은 f(x)가 호출될 때마다 다른 값이 반환이 됩니다. self.loss 가 호출될 때 self.predict 함수가 호출되면서 변경된 W 값이 적용이되어 self.predict 값이 변경되고 따라서 cross_entropy_error 값이 바뀌게 되는 것입니다.

예를 들어봅니다.

In [32]: from two_layer_net import TwoLayerNet

In [33]: net = TwoLayerNet(input_size=784, hidden_size=100, output_size=10)
   ....: for key, val in net.params.items():
   ....:   print('{}: {}'.format(key, val.shape))
   ....: 
W1: (784, 100)
b1: (100,)
W2: (100, 10)
b2: (10,)

미니배치 학습 구현

다음 코드를 실행하면 상당한 시간이 걸릴 수도 있습니다.

ch04/train_neuralnet.py

import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

# 하이퍼파라미터
iters_num = 10000  # 반복 횟수를 적절히 설정한다.
train_size = x_train.shape[0]
batch_size = 100   # 미니배치 크기
learning_rate = 0.1

train_loss_list = []

for i in range(iters_num):
    # 미니배치 획득
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 기울기 계산
    #grad = network.numerical_gradient(x_batch, t_batch)
    grad = network.gradient(x_batch, t_batch)
    
    # 매개변수 갱신
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    # 학습 경과 기록
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)

시험데이터 평가

밝게 표시된 부분이 새로 추가된 부분입니다.

ch04/train_neuralnet.py

import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

# 하이퍼파라미터
iters_num = 10000  # 반복 횟수를 적절히 설정한다.
train_size = x_train.shape[0]
batch_size = 100   # 미니배치 크기
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

# 1에폭당 반복 수
iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    # 미니배치 획득
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 기울기 계산
    #grad = network.numerical_gradient(x_batch, t_batch)
    grad = network.gradient(x_batch, t_batch)
    
    # 매개변수 갱신
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    # 학습 경과 기록
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    # 1에폭당 정확도 계산
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

퍼셉트론 학습

데이터는 첫번째는 $x^1 = (x_1, x_2)$ 이고 $i$ 번째는 $x^i = (x_1^i, x_2^i)$ 와 같이 표시하며 $N$ 개로 이루어졌다고 가정합니다. 여기에 대응되는 레이블(타겟)은 $t^i$으로 표시합니다.

\[x^1 = (x_1^1, x_2^1), x^2 = (x_1^2, x_2^2), \ldots, x^N = (x_1^N, x_2^N)\]

활성화함수는 계단함수를 사용합니다.

\[\begin{split}y^i = h(a^i) = \begin{cases} 1, & a^i \ge 0 \\ -1, & a^i < 0 \end{cases}\end{split}\]

여기서

\[a^i = w_1 x_1^i + w_2 x_2^i + b\]

입니다. $a^i > 0$ 이면 $y^i = 1$ 이고 $a^i < 0$ 이면 $y^i = -1$ 이므로 만일 우리가 찾는 퍼셉트론이라면 $y^i a^i \ge 0$이 되고 더 많은 $x^i$에 대해서 $\sum_i y^i a^i$는 증가하게 됩니다. 그러므로 $\sum_i y^i a^i$가 최대가 되도록 $w, b$를 구하는 문제가 되고 $-\sum_i y^i a^i$가 최소가 되도록 하는 문제와 같습니다.

따라서 손실함수를 다음과 같이 정의합니다.

\[L(w_1, w_2, b) = - \sum_i^N y^i(w_1 x_1^i + w_2 x_2^i + b)\]

이것의 그래디언트는 다음과 같습니다.

\[\frac{\partial L}{\partial w_1} = - \sum_i^N y^i x_1^i, \quad \frac{\partial L}{\partial w_2} = - \sum_i^N y^i x_2^i, \quad \frac{\partial L}{\partial b} = - \sum_i^N y^i\]

여기서 $y^i = t^i$ 일 때는 손실에 포함시킬 필요가 없으므로 $y^i \ne t^i$ 일 때만 포함시키면됩니다. 그러면 각각의 손실량은 $y^i a^i < 0$이 되어 손실함수 전체는 항상 0보다 크거나 같은 것이 됩니다.

따라서 손실함수를 다음과 같이 쓸 수 있습니다.

\[L(w_1, w_2, b) = - \sum_i^N (t^i - y^i)(w_1 x_1^i + w_2 x_2^i + b)\]

즉, $y^i = t^i$일 때는 $y^i - t^i = 0$이 되어 손실량에 포함되지 않게 됩니다. 따라서 그래디언트도 다음과 같이 표현됩니다.

\[\frac{\partial L}{\partial w_1} = - \sum_i^N (t^i - y^i) x_1^i, \quad \frac{\partial L}{\partial w_2} = - \sum_i^N (t^i - y^i) x_2^i, \quad \frac{\partial L}{\partial b} = - \sum_i^N (t^i - y^i)\]

경사하강법을 사용한다면 다음과 같이 쓸 수 있습니다.

\[\begin{split}(w_1^{n+1}, w_2^{n+1}, b^{n+1}) = (w_1^{n}, w_2^{n}, b^{n}) - \eta \cdot \nabla L \\ \nabla L = \left(\frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, \frac{\partial L}{\partial b} \right)\end{split}\]

SGD를 사용한 코드는 다음과 같습니다.

In [34]: class Perceptron:
   ....: 
   ....:   def __init__(self, dim_of_input, threshold=100, learning_rate=0.01):
   ....:     self.threshold = threshold
   ....:     self.learning_rate = learning_rate
   ....:     self.W = np.zeros(dim_of_input + 1)
   ....: 
   ....:   def predict(self, x):
   ....:     a = np.dot(x, self.W[1:]) + self.W[0]
   ....:     if a > 0:
   ....:       return 1
   ....:     else:
   ....:       return -1
   ....: 
   ....:   def train(self, X, T):
   ....:     for _ in range(self.threshold):
   ....:       for x, t in zip(X, T):
   ....:         y = self.predict(x)
   ....:         self.W[1:] += self.learning_rate * (t - y) * x
   ....:         self.W[0] += self.learning_rate * (t - y)
   ....: 

AND 게이트에 대해서 적용해봅니다.

In [35]: X = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
   ....: T = np.array([1, -1, -1, -1])
   ....: 

In [36]: perceptron = Perceptron(2)
   ....: perceptron.train(X, T)
   ....: 
   ....: print(perceptron.W)
   ....: 
   ....: x1 = np.array([1, 1])
   ....: y1 = perceptron.predict(x1)
   ....: print(y1)
   ....: 
   ....: x2 = np.array([0, 1])
   ....: y2 = perceptron.predict(x2)
   ....: print(y2)
   ....: 
[-0.04  0.02  0.04]
1
-1

직접하기

OR, NAND, XOR 게이트를 구해보세요.

참조 사이트

연습문제

MNIST 데이터 중 0, 2, 4, 6, 8번째 데이터에 대한 MSE를 각각 구하여 출력하고 그들의 평균 MSE를 구하세요. 3장(신경망)에서 사용했던 neuralnet_mnist.py 파일을 참조해서 프로그래밍을 완성 하세요.
위 문제와 같은 데이터에 대해서 교차엔트로피 오차를 각각 구하여 출력하고, 평균 교차엔트로피 오차를 구하세요.
3장 신경망 연습문제 1, 2, 3번 문제를 TwoLayerNet 클래스를 이용해서 구해보세요. 다음과 같은 TwoLayerPerceptron 클래스를 만들어서 구해보세요.

class TwoLayerPerceptron:
  def __init__(self, input_size=2, hidden_size=15, output_size=2, train_size=5, batch_size=3, iter_nums=500, learning_rate=0.5):
    """
    Keyword arguments:
    input_size -- 입력변수의 갯수
    hidden_size -- 은닉층 크기
    output_size -- 결과값 갯수
    train_size -- 훈련 입력값의 갯수
    batch_size -- 훈련 배치 갯수
    iter_nums -- 반복 횟수
    learning_rate -- 학습률
    """
    pass

  def train(self, x, t):
    # x는 2차원 배열, t는 1차원 label 배열; 훈련 메소드
    pass

  def predict(self, x):
    pass

  def accuracy(self, x, t):
    """정확도
    """
    pass

  def draw(self):
    """정확도 그래프 그리기
    """
    pass

은닉층의 갯수, 학습률 등을 변화시키면서 정확도를 높여보세요.
결과에 대해서 이야기해 보세요.